Aufgaben:Aufgabe 4.15Z: MSK–Grundimpuls und MSK-Spektrum: Unterschied zwischen den Versionen
Aus LNTwww
Safwen (Diskussion | Beiträge) |
|||
| (17 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulationsverfahren/Nichtlineare_digitale_Modulation |
}} | }} | ||
| − | [[Datei:P_ID1744__Mod_Z_4_14.png|right|]] | + | [[Datei:P_ID1744__Mod_Z_4_14.png|right|frame|MSK–Grundimpuls und –Spektrum]] |
| − | Der zur Realisierung der [ | + | Der zur Realisierung der [[Modulationsverfahren/Nichtlineare_digitale_Modulation#Realisierung_der_MSK_als_Offset.E2.80.93QPSK|MSK mittels Offset–QPSK]] stets erforderliche Grundimpuls hat die in der Grafik oben dargestellte Form: |
| − | $$g_{\rm MSK}(t) = \left\{ \begin{array}{l} g_0 \cdot \cos ( | + | :$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} | t | \le T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$ |
| − | + | Darunter gezeichnet ist die Spektralfunktion $G(f)$, also die [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|Fouriertransformierte]] von $g(t)$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | '' | + | Die dazugehörige Gleichung soll in dieser Aufgabe ermittelt werden, wobei zu berücksichtigen ist: |
| + | :$$g(t) = c(t) \cdot r(t)\hspace{0.05cm}.$$ | ||
| + | Hierbei sind folgende Abkürzungen verwendet: | ||
| + | * $c(t)$ ist eine Cosinusschwingung mit Amplitude $1$ und (noch zu bestimmender) Frequenz $f_0$. | ||
| + | * $r(t)$ ist eine Rechteckfunktion mit der Amplitude $g_0$ und der Dauer $2T$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Nichtlineare_digitale_Modulation|Nichtlineare digitale Modulation]]. | ||
| + | *Bezug genommen wird insbesondere auf den Abschnitt [[Modulationsverfahren/Nichtlineare_digitale_Modulation#Realisierung_der_MSK_als_Offset.E2.80.93QPSK|Realisierung der MSK als Offset-QPSK]]. | ||
| + | |||
| + | *Das hier gewonnene Ergebnis wird auch in der [[Aufgaben:4.15_MSK_im_Vergleich_mit_BPSK_und_QPSK|Aufgabe 4.15]] verwendet. | ||
| Zeile 18: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie ist die Frequenz $f_0$ | + | {Wie ist die Frequenz $f_0$ der Cosinusschwingung $c(t)$ zu wählen, damit $g(t) = c(t) · r(t)$ gilt? |
|type="{}"} | |type="{}"} | ||
| − | $f_0$ | + | $f_0 \ = \ $ { 0.25 3% } $\ \cdot 1/T$ |
| − | {Wie lautet das Spektrum $R(f)$ | + | {Wie lautet das Spektrum $R(f)$ der Rechteckfunktion $r(t)$? Welcher Spektralwert tritt bei $f = 0$ auf? |
|type="{}"} | |type="{}"} | ||
| − | $R(f=0)$ | + | $R(f=0) \ = \ $ { 2 3% } $\ \cdot g_0 \cdot T$ |
| − | {Berechnen Sie das Spektrum $G(f)$, insbesondere den Spektralwert bei f = 0. | + | {Berechnen Sie das Spektrum $G(f)$ des MSK–Impuses $g(t)$, insbesondere den Spektralwert bei $f = 0$. |
|type="{}"} | |type="{}"} | ||
| − | $G(f = 0)$ | + | $G(f=0) \ = \ $ { 1.273 3% } $\ \cdot g_0 \cdot T$ |
| − | {Fassen Sie das Ergebnis | + | {Fassen Sie das Ergebnis der Teilaufgabe '''(3)''' in einem Term zusammen. Bei welcher Frequenz $f_1$ besitzt $G(f)$ seine erste Nullstelle? |
|type="{}"} | |type="{}"} | ||
| − | $f_1$ | + | $f_1 \ = \ $ { 0.75 3% } $\ \cdot 1/T$ |
</quiz> | </quiz> | ||
| Zeile 38: | Zeile 51: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Die Periodendauer des Cosinussignals muss $T_0 = 4T$ sein. Damit ist die Frequenz $f_0 = 1/T_0\hspace{0.15cm}\underline {= 0.25} · 1/T$. |
| + | |||
| + | |||
| + | '''(2)''' Die Spektralfunktion eines Rechteckimpulses der Höhe $g_0$ und der Dauer $ 2T$ lautet: | ||
| + | :$$R(f) = g_0 \cdot 2 T \cdot {\rm si} ( \pi f \cdot 2T )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si} (x) = \sin(x)/x \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}R(f = 0) \hspace{0.15cm}\underline {= 2} \cdot g_0 \cdot T\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Aus $g(t) = c(t) · r(t)$ folgt nach dem Faltungssatz: $ G(f) = C(f) \star R(f)\hspace{0.05cm}.$ | ||
| + | *Die Spektralfunktion $C(f)$ besteht aus zwei Diracfunktionen bei $± f_0$, jeweils mit dem Gewicht $1/2$. Daraus folgt: | ||
| + | :$$ G(f) = 2 \cdot g_0 \cdot T \cdot \big [ 1/2 \cdot \delta (f - f_0 ) + 1/2 \cdot \delta (f + f_0 )\big ] \star {\rm si} ( 2 \pi f T )= g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi T \cdot (f - f_0 ) ) + {\rm si} ( 2 \pi T \cdot (f + f_0 ) ) \big ] \hspace{0.05cm}.$$ | ||
| + | *Mit dem Ergebnis $f_0 = 1/(4T)$ der Teilaufgabe '''(1)''' gilt weiter: | ||
| + | :$$G(f) = g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi f T - \pi / 2 ) + {\rm si} ( 2 \pi f T + \pi / 2) \big ]$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} G(f = 0) = g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \big [ {\rm si} ( - \pi/2 ) + {\rm si} ( +\pi/2 ) \big ] = 2 \cdot g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} {\rm si} ( \pi/2 ) = 2 \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \frac {{\rm sin}({\pi}/{2}) } { {\pi}/{2} } ={4}/{\pi} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{0.15cm}\underline {\approx 1.273} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T .$$ | ||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''(4)''' Schreibt man die $\rm si$–Funktion aus, so erhält man mit $\sin (α ± π/2) = ± \cos(α)$: |
| − | $ | + | :$$G(f) = g_0 \cdot T \cdot \left [ \frac{{\rm sin} ( 2 \pi f T - \pi / 2 )}{2 \pi f T - \pi / 2 } + \frac{{\rm sin} ( 2 \pi f T + \pi / 2 )}{2 \pi f T + \pi / 2 } \right ]= g_0 \cdot T \cdot \frac {2}{\pi}\cdot\left [ \frac{-{\rm cos} ( 2 \pi f T )}{4 f T - 1 } + \frac{{\rm cos} ( 2 \pi f T )}{4 f T + 1 } \right ]$$ |
| − | + | :$$\Rightarrow \hspace{0.3cm} G(f) = g_0 \cdot T \cdot \frac {2}{\pi}\cdot \frac{(1+4 f T ) \cdot {\rm cos} ( 2 \pi f T )+ (1-4 f T ) \cdot {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 } = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$ | |
| − | $$ G(f) = | ||
| − | |||
| − | |||
| − | |||
| − | $$\Rightarrow \hspace{0.3cm} G(f | ||
| − | |||
| − | + | *Die Nullstellen von $G(f)$ werden allein durch die Cosinusfunktion im Zähler bestimmt und würden bei den Frequenzen $f · T = 0.25,\ 0.75,\ 1.25,$ ... liegen. | |
| − | + | *Allerdings wird die erste Nullstelle bei $f · T = 0.25$ durch die gleichzeitige Nullstelle des Nenners aufgehoben. Deshalb gilt: | |
| − | + | :$$f_1 \hspace{0.15cm}\underline {= 0.75} \cdot 1/T \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | Die Nullstellen von $G(f)$ werden allein durch die Cosinusfunktion im Zähler bestimmt und würden bei den Frequenzen f · T = 0.25, 0.75, 1.25, ... liegen. Allerdings wird die erste Nullstelle bei $f · T = 0.25$ durch die gleichzeitige Nullstelle des Nenners aufgehoben. Deshalb gilt: | ||
| − | $$f_1 \hspace{0.15cm}\underline {= 0.75} \cdot 1/T \hspace{0.05cm}.$$ | ||
| Zeile 67: | Zeile 80: | ||
| − | [[Category:Aufgaben zu Modulationsverfahren|^4.4 Nichtlineare | + | [[Category:Aufgaben zu Modulationsverfahren|^4.4 Nichtlineare digitale Modulation^]] |
Aktuelle Version vom 24. April 2020, 13:23 Uhr
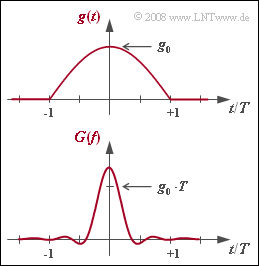
Der zur Realisierung der MSK mittels Offset–QPSK stets erforderliche Grundimpuls hat die in der Grafik oben dargestellte Form:
- $$g_{\rm MSK}(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} | t | \le T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$
Darunter gezeichnet ist die Spektralfunktion $G(f)$, also die Fouriertransformierte von $g(t)$.
Die dazugehörige Gleichung soll in dieser Aufgabe ermittelt werden, wobei zu berücksichtigen ist:
- $$g(t) = c(t) \cdot r(t)\hspace{0.05cm}.$$
Hierbei sind folgende Abkürzungen verwendet:
- $c(t)$ ist eine Cosinusschwingung mit Amplitude $1$ und (noch zu bestimmender) Frequenz $f_0$.
- $r(t)$ ist eine Rechteckfunktion mit der Amplitude $g_0$ und der Dauer $2T$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Nichtlineare digitale Modulation.
- Bezug genommen wird insbesondere auf den Abschnitt Realisierung der MSK als Offset-QPSK.
- Das hier gewonnene Ergebnis wird auch in der Aufgabe 4.15 verwendet.
Fragebogen
Musterlösung
(1) Die Periodendauer des Cosinussignals muss $T_0 = 4T$ sein. Damit ist die Frequenz $f_0 = 1/T_0\hspace{0.15cm}\underline {= 0.25} · 1/T$.
(2) Die Spektralfunktion eines Rechteckimpulses der Höhe $g_0$ und der Dauer $ 2T$ lautet:
- $$R(f) = g_0 \cdot 2 T \cdot {\rm si} ( \pi f \cdot 2T )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si} (x) = \sin(x)/x \hspace{0.3cm} \Rightarrow \hspace{0.3cm}R(f = 0) \hspace{0.15cm}\underline {= 2} \cdot g_0 \cdot T\hspace{0.05cm}.$$
(3) Aus $g(t) = c(t) · r(t)$ folgt nach dem Faltungssatz: $ G(f) = C(f) \star R(f)\hspace{0.05cm}.$
- Die Spektralfunktion $C(f)$ besteht aus zwei Diracfunktionen bei $± f_0$, jeweils mit dem Gewicht $1/2$. Daraus folgt:
- $$ G(f) = 2 \cdot g_0 \cdot T \cdot \big [ 1/2 \cdot \delta (f - f_0 ) + 1/2 \cdot \delta (f + f_0 )\big ] \star {\rm si} ( 2 \pi f T )= g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi T \cdot (f - f_0 ) ) + {\rm si} ( 2 \pi T \cdot (f + f_0 ) ) \big ] \hspace{0.05cm}.$$
- Mit dem Ergebnis $f_0 = 1/(4T)$ der Teilaufgabe (1) gilt weiter:
- $$G(f) = g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi f T - \pi / 2 ) + {\rm si} ( 2 \pi f T + \pi / 2) \big ]$$
- $$\Rightarrow \hspace{0.3cm} G(f = 0) = g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \big [ {\rm si} ( - \pi/2 ) + {\rm si} ( +\pi/2 ) \big ] = 2 \cdot g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} {\rm si} ( \pi/2 ) = 2 \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \frac {{\rm sin}({\pi}/{2}) } { {\pi}/{2} } ={4}/{\pi} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{0.15cm}\underline {\approx 1.273} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T .$$
(4) Schreibt man die $\rm si$–Funktion aus, so erhält man mit $\sin (α ± π/2) = ± \cos(α)$:
- $$G(f) = g_0 \cdot T \cdot \left [ \frac{{\rm sin} ( 2 \pi f T - \pi / 2 )}{2 \pi f T - \pi / 2 } + \frac{{\rm sin} ( 2 \pi f T + \pi / 2 )}{2 \pi f T + \pi / 2 } \right ]= g_0 \cdot T \cdot \frac {2}{\pi}\cdot\left [ \frac{-{\rm cos} ( 2 \pi f T )}{4 f T - 1 } + \frac{{\rm cos} ( 2 \pi f T )}{4 f T + 1 } \right ]$$
- $$\Rightarrow \hspace{0.3cm} G(f) = g_0 \cdot T \cdot \frac {2}{\pi}\cdot \frac{(1+4 f T ) \cdot {\rm cos} ( 2 \pi f T )+ (1-4 f T ) \cdot {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 } = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$
- Die Nullstellen von $G(f)$ werden allein durch die Cosinusfunktion im Zähler bestimmt und würden bei den Frequenzen $f · T = 0.25,\ 0.75,\ 1.25,$ ... liegen.
- Allerdings wird die erste Nullstelle bei $f · T = 0.25$ durch die gleichzeitige Nullstelle des Nenners aufgehoben. Deshalb gilt:
- $$f_1 \hspace{0.15cm}\underline {= 0.75} \cdot 1/T \hspace{0.05cm}.$$