Aufgaben:Aufgabe 4.6Z: Ortskure bei Phasenmodulation: Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
Das modulierte Signal lautet bei Phasenmodulation: | Das modulierte Signal lautet bei Phasenmodulation: | ||
:$$s(t) = s_0 \cdot {\cos} ( \omega_{\rm T}\hspace{0.05cm} t + \eta \cdot q(t)).$$ | :$$s(t) = s_0 \cdot {\cos} ( \omega_{\rm T}\hspace{0.05cm} t + \eta \cdot q(t)).$$ | ||
| − | Hierbei bezeichnet $\eta$ den so genannten Modulationsindex. Auch die konstante Hüllkurve $s_0$ sei eine dimensionslose Größe, die im Folgenden zu 2 gesetzt wird (siehe Grafik). | + | Hierbei bezeichnet $\eta$ den so genannten Modulationsindex. Auch die konstante Hüllkurve $s_0$ sei eine dimensionslose Größe, die im Folgenden zu $s_0 = 2$ gesetzt wird (siehe Grafik). |
Ersetzt man in dieser Gleichung die Cosinus– durch die komplexe Exponentialfunktion, so kommt man zum analytischen Signal | Ersetzt man in dieser Gleichung die Cosinus– durch die komplexe Exponentialfunktion, so kommt man zum analytischen Signal | ||
| Zeile 23: | Zeile 23: | ||
*Sie können Ihre Lösung mit dem folgenden Interaktionsmodul überprüfen: | *Sie können Ihre Lösung mit dem folgenden Interaktionsmodul überprüfen: | ||
[[Ortskurve – Darstellung des äquivalenten Tiefpass-Signals]] | [[Ortskurve – Darstellung des äquivalenten Tiefpass-Signals]] | ||
| − | |||
| − | |||
| Zeile 30: | Zeile 28: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lautet die Betragsfunktion $a(t) = |s_{TP}(t)|$? Welcher Wert gilt für $t = 0$? | + | {Wie lautet die Betragsfunktion $a(t) = |s_{\rm TP}(t)|$? Welcher Wert gilt für $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $a(t = 0)$ = { 2 3% } | + | $a(t = 0)$ = { 2 3% } |
| − | {Zwischen welchen | + | {Zwischen welchen Extremwerten $\phi_{\rm min}$ und $\phi_{\rm max}$ schwankt die Phase $\phi (t)$? |
|type="{}"} | |type="{}"} | ||
| − | $\phi_{min}$ = | + | $\phi_{\rm min}$ = { -93--87 } $\text{Grad}$ |
| − | $\phi_{min}$ = { 180 3% } $\text{Grad}$ | + | $\phi_{\rm min}$ = { 180 3% } $\text{Grad}$ |
| − | {Bestimmen Sie aus der Phasenfunktion $\phi (t)$ den Modulationsindex. | + | {Bestimmen Sie aus der Phasenfunktion $\phi (t)$ den Modulationsindex $\eta$. |
|type="{}"} | |type="{}"} | ||
| − | $\eta$ = { 3.1415 3% } | + | $\eta$ = { 3.1415 3% } |
| Zeile 49: | Zeile 47: | ||
|type="[]"} | |type="[]"} | ||
- Aus $q(t) = –0.5 = \text{const}$. folgt $s(t) = s_0 \cdot \cos (\omega_T \cdot t)$. | - Aus $q(t) = –0.5 = \text{const}$. folgt $s(t) = s_0 \cdot \cos (\omega_T \cdot t)$. | ||
| − | + Bei einem Rechtecksignal $q(t) | + | + Bei einem Rechtecksignal $q(t)$ (nur zwei mögliche Signalwerte $\pm 0.5$) entartet die Ortskurve zu zwei Punkten. |
| − | + Mit den Signalwerten $\pm 1$ | + | + Mit den Signalwerten $\pm 1$ (''Hinweis'': Die Angabe $q_{\rm min} = –0.5$ gilt dann nicht) wird die Ortskurve zu einem Punkt: $s_{\rm TP}(t) = –s_0$. |
Version vom 22. Januar 2017, 15:49 Uhr
Wir gehen hier von einem Nachrichtensignal $q(t)$ aus, das normiert (dimensionslos) betrachtet wird. Der Maximalwert dieses Signal ist $q_{\rm max} = 1$ und der minimale Signalwert beträgt $q_{\rm min} = –0.5$. Ansonsten ist über $q(t)$ nichts bekannt.
Das modulierte Signal lautet bei Phasenmodulation:
- $$s(t) = s_0 \cdot {\cos} ( \omega_{\rm T}\hspace{0.05cm} t + \eta \cdot q(t)).$$
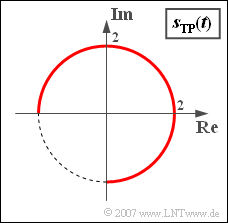
Hierbei bezeichnet $\eta$ den so genannten Modulationsindex. Auch die konstante Hüllkurve $s_0$ sei eine dimensionslose Größe, die im Folgenden zu $s_0 = 2$ gesetzt wird (siehe Grafik).
Ersetzt man in dieser Gleichung die Cosinus– durch die komplexe Exponentialfunktion, so kommt man zum analytischen Signal
- $$s_{\rm +}(t) = s_0\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}( \omega_{\rm T} \hspace{0.05cm}\cdot \hspace{0.05cm} t + \eta \hspace{0.05cm} \cdot \hspace{0.05cm} q(t)) }.$$
Daraus kann man das in der Grafik skizzierte äquivalente TP-Signal wie folgt berechnen:
- $$s_{\rm TP}(t) = s_{\rm +}(t) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot\hspace{0.05cm} \omega_{\rm T} \hspace{0.05cm}\cdot\hspace{0.05cm} t } = s_0\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} \eta \hspace{0.05cm} \cdot \hspace{0.05cm} q(t) }.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Sie können Ihre Lösung mit dem folgenden Interaktionsmodul überprüfen:
Ortskurve – Darstellung des äquivalenten Tiefpass-Signals
Fragebogen
Musterlösung
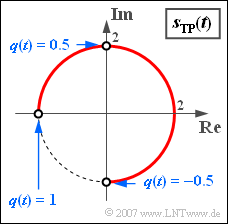
2. Aus der Grafik ist zu erkennen, dass $\phi_{min} \underline{= –\pi /2 (–90°)}$ und $\phi_{max} \underline{= +\pi (180°)}$ ist.
3. Allgemein gilt folgender Zusammenhang:
- $$s_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\cdot \hspace{0.05cm} \phi(t)}.$$
Ein Vergleich mit der gegebenen Funktion liefert:
- $$\phi(t) = \eta \cdot q(t).$$
Der maximale Phasenwert $\phi_{max} = \pi (180°)$ ergibt sich für die Signalamplitude $q_{max} = 1$. Daraus folgt direkt $\underline{\eta = \pi}$. Dieser Modulationsindex wird durch die Werte $\phi_{min} = –\pi /2$ und $q_{min} = –0.5$ bestätigt.
4. Ist $q(t) = \text{const.} = –0.5$, so ist die Phasenfunktion ebenfalls konstant:
- $$\phi(t) = \eta \cdot q(t) = - \frac{\pi}{2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{\rm TP}(t) = - {\rm j} \cdot s_0 = - 2{\rm j}.$$
Somit gilt für das tatsächliche, physikalische Signal:
- $$s(t) = s_0 \cdot {\cos} ( \omega_{\rm T}\hspace{0.05cm} t - \frac{\pi}{2}) = 2 \cdot {\sin} ( \omega_{\rm T} \hspace{0.05cm} t ).$$
Dagegen führt $q(t) = 0.5$ zu $\phi (t) = \pi /2$ und $s_{TP}(t) = 2j$. Ist $q(t)$ ein Rechtecksignal, das abwechselnd die Werte $+0.5$ und $–0.5$ annimmt, besteht somit die Ortskurve nur aus zwei Punkten auf der imaginären Achse, und zwar unabhängig davon, wie lange die Intervalle mit $+0.5$ und $–0.5$ dauern.
Gilt dagegen $q(t) = \pm 1$, so ergeben sich rein formal die möglichen Phasenwerte $+\pi$ und $–\pi$, die aber identisch sind. Die „Ortskurve” besteht dann nur aus einem einzigen Punkt: $s_{TP}(t) = – s_0 \Rightarrow$ das Signal $s(t)$ ist „minus-cosinusförmig”.
Richtig sind der zweite und der dritte Lösungsvorschlag.