Aufgaben:Aufgabe 1.8Z: Cosinus-Quadrat-Tiefpass: Unterschied zwischen den Versionen
| Zeile 10: | Zeile 10: | ||
* Für $f \cdot T \ge 1$ ist $H(f) = 0$. | * Für $f \cdot T \ge 1$ ist $H(f) = 0$. | ||
*Im inneren Bereich gilt $H(f) = \cos^2(f \cdot T \cdot {\pi}/{ 2} ) .$ | *Im inneren Bereich gilt $H(f) = \cos^2(f \cdot T \cdot {\pi}/{ 2} ) .$ | ||
| + | |||
Anzumerken ist, dass die äquivalente Bandbreite $\Delta f = 1{\Delta t}$ betragen soll. Damit ist die äquivalente ${\Delta t}$ der Impulsantwort ebenfalls $T$ und man erhält: | Anzumerken ist, dass die äquivalente Bandbreite $\Delta f = 1{\Delta t}$ betragen soll. Damit ist die äquivalente ${\Delta t}$ der Impulsantwort ebenfalls $T$ und man erhält: | ||
| − | :$$y(t) = T \cdot h(t) = {\rm si}(\pi \cdot | + | :$$y(t) = T \cdot h(t) = {\rm si}(\pi \cdot {t}/{T} )\cdot \frac |
{\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2}.$$ | {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2}.$$ | ||
Zu beachten ist, dass das Ausgangssignal $y(t)$ im Gegensatz zur Impulsantwort $h(t)$ ohne Einheit ist. Durch Anwendung trigonomischer Umformungen kann dieses Signal auch wie folgt dargestellt werden: | Zu beachten ist, dass das Ausgangssignal $y(t)$ im Gegensatz zur Impulsantwort $h(t)$ ohne Einheit ist. Durch Anwendung trigonomischer Umformungen kann dieses Signal auch wie folgt dargestellt werden: | ||
| − | $$y(t) = | + | $$y(t) = {\pi}/{4} \cdot {\rm si}(\pi \cdot {t}/{T} )\cdot |
\left[ {\rm si}\left(\pi \cdot \left({t}/{T}+ 0.5 \right) | \left[ {\rm si}\left(\pi \cdot \left({t}/{T}+ 0.5 \right) | ||
\right)+ {\rm si}\left(\pi \cdot \left({t}/{T}- 0.5 \right) | \right)+ {\rm si}\left(\pi \cdot \left({t}/{T}- 0.5 \right) | ||
| Zeile 58: | Zeile 59: | ||
$H_E(f=0) \ = $ { 1 1% } | $H_E(f=0) \ = $ { 1 1% } | ||
$H_E(f=0.5/T) \ = $ { 0.785 1% } | $H_E(f=0.5/T) \ = $ { 0.785 1% } | ||
| − | $H_E(f=1/T) \ = $ | + | $H_E(f=1/T) \ = $ { 0. } |
| Zeile 66: | Zeile 67: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Aus der ersten Gleichung auf der Angabenseite folgt aufgrund der si–Funktion direkt $y(t = 0) = 1$ und $y(t = T) = y(t = 2T) = ... =0$. Auch aus der zweiten Gleichung erhält man diese Ergebnisse, beispielsweise | |
| − | + | $$y(t = 0) = {\pi}/{4} \cdot {\rm si}(0)\cdot \left[ {\rm | |
| − | si}(\pi/2)+ {\rm si}(-\pi/2)\right] | + | si}(\pi/2)+ {\rm si}(-\pi/2)\right] |
| − | + | {\pi}/{2} \cdot {\rm si}(\pi/2) = {\pi}/{2} \cdot | |
\frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{= 1},$$ | \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{= 1},$$ | ||
| − | + | $$y(t = T) \hspace{0.15cm}=\hspace{0.15cm}{\pi}/{4} \cdot {\rm si}(\pi)\cdot \left[ {\rm | |
si}(3\pi/2)+ {\rm si}(\pi/2)\right] \hspace{0.15cm}\underline{= 0}.$$ | si}(3\pi/2)+ {\rm si}(\pi/2)\right] \hspace{0.15cm}\underline{= 0}.$$ | ||
| − | + | ||
| − | + | '''(2)''' Zur Berechnung dieser Signalwerte ist die zweite Darstellung besser geeignet: | |
| + | $$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)\cdot \left[ {\rm | ||
si}(\pi)+ {\rm si}(0)\right].$$ | si}(\pi)+ {\rm si}(0)\right].$$ | ||
| − | + | Mit si(0) = 1 und si(π) = 0 erhält man so: | |
| − | + | $$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)= {\pi}/{4} | |
\cdot \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{ = 0.5}.$$ | \cdot \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{ = 0.5}.$$ | ||
| − | + | In analoger Weise ergibt sich für <i>t</i> = 1.5<i>T</i>: | |
| − | :$$y(t = 1.5T) = | + | :$$y(t = 1.5T) = {\pi}/{4} \cdot {\rm si}(3\pi/2)\cdot \left[ |
{\rm si}(2\pi)+ {\rm si}(\pi)\right] \hspace{0.15cm}\underline{ = 0}.$$ | {\rm si}(2\pi)+ {\rm si}(\pi)\right] \hspace{0.15cm}\underline{ = 0}.$$ | ||
| − | + | Hierbei ist ${\rm si}(\pi) = {\rm si}(\pi) = 0$ berücksichtigt. Zu den Zeitpunkten $t/T = 2.5, 3.5, ... $ gilt ebenfalls $y(t) = 0$, wie die folgende Grafik zeigt. | |
| − | [[Datei:P_ID871__LZI_Z_1_8_b.png| | + | [[Datei:P_ID871__LZI_Z_1_8_b.png|Ausgangssignal des Cosinus–Quadrat–Tiefpasses]] |
| + | |||
| − | + | '''(3)''' Für große Werte von $t$ gilt näherungsweise (wenn man die „1” im Nenner vernachlässigt): | |
| − | :$$y(t) = \frac {\sin(\pi \cdot t / T )\cdot \cos(\pi \cdot t / T | + | :$$y(t)= {\rm si}(\pi \cdot {t}/{T} )\cdot \frac |
| + | {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2} \approx \frac {\sin(\pi \cdot t / T )\cdot \cos(\pi \cdot t / T | ||
)}{ - (\pi \cdot t/T )(2 \cdot t/T )^2} = - \frac {\sin(2\pi | )}{ - (\pi \cdot t/T )(2 \cdot t/T )^2} = - \frac {\sin(2\pi | ||
\cdot t / T )}{ 8 \pi \cdot( t/T )^3}.$$ | \cdot t / T )}{ 8 \pi \cdot( t/T )^3}.$$ | ||
| − | + | Hierbei ist berücksichtigt, dass $\sin(\alpha) \cdot \cos(\alpha) = \sin(2\alpha)/2$ ist. Zum Zeitpunkt $t = 10.75 T$ gilt dann: | |
:$$\sin(2\pi \cdot t / T ) = \sin (21.5\pi)= \sin (1.5\pi) = -1.$$ | :$$\sin(2\pi \cdot t / T ) = \sin (21.5\pi)= \sin (1.5\pi) = -1.$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm} y(t = 10.75 T) = \frac {1 }{ 8 \pi \cdot( 10.75 )^3} \hspace{0.15cm}\underline{= | + | :$$\Rightarrow \hspace{0.3cm} y(t = 10.75 T) = \frac {1 }{ 8 \pi \cdot( 10.75 )^3} \hspace{0.15cm}\underline{= 32} |
| − | \cdot 10^{- | + | \cdot 10^{-6}.$$ |
| − | : | + | [[Datei:P_ID872__LZI_Z_1_8_d.png|right|Gesuchter Empfängerfrequenzgang]] |
| − | + | '''(4)''' Der Empfängerfrequenzgang lautet für$|f \cdot T| \le 1$ : | |
| + | $$H_{\rm E}(f) = \frac{H(f)}{H_{\rm S}(f)}= \frac{\cos^2(\pi f T | ||
/2)}{{\rm si}(\pi fT)}.$$ | /2)}{{\rm si}(\pi fT)}.$$ | ||
| − | + | Dieser Funktionsverlauf ist in der Grafik dargestellt. Für die gesuchten Stützwerte gilt: | |
| − | + | $$H_{\rm E}(f = 0) = \frac{\cos^2(0)}{{\rm si}(0)} \hspace{0.15cm}\underline{ = 1},$$ | |
| − | + | $$H_{\rm E}(f = {0.5}/T \hspace{-0.15cm} = \hspace{-0.15cm} \frac{\cos^2(\pi/4)}{{\rm si}(\pi/2)}= (\sqrt{2} / 2)^2 \cdot \frac{\pi}{2} | |
| − | |||
| − | |||
= \hspace{-0.15cm} \frac{\pi}{4}\hspace{0.15cm}\underline{ \approx 0.785},$$ | = \hspace{-0.15cm} \frac{\pi}{4}\hspace{0.15cm}\underline{ \approx 0.785},$$ | ||
| − | + | $$H_{\rm E}(f = {1}/{T}) = \frac{\cos^2(\pi/2)}{{\rm si}(\pi)} = "0/0"\hspace{0.15cm}\underline{= 0}.$$ | |
| − | + | Bei diesem Ergebnis ist berücksichtigt, dass im gesamten Frequenzbereich $H_{\rm S}(f) \ge H(f) $ gilt. Eigentlich müsste der zuletzt berechnete Wert durch einen Grenzübergang mathematisch-exakt bestimmt werden. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 30. Januar 2017, 13:22 Uhr
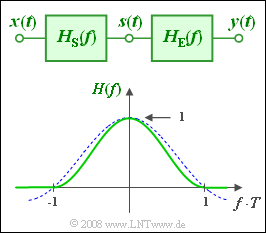
Bei der Untersuchung von Digitalsystemen geht man häufig von einem diracförmigen Eingangssignal $x(t) = T \cdot \delta(t)$ aus, so dass $X(f) = T$ gilt. Das Ausgangsspektrum $Y(f)$ ist dann formgleich mit dem Gesamtfrequenzgang von Sende– und Empfangsfilter:
- $$H(f) = H_{\rm S}(f) \cdot H_{\rm E}(f).$$
Dieser wird häufig als $cos^2$-förmig angenommen (siehe Grafik):
- Für $f \cdot T \ge 1$ ist $H(f) = 0$.
- Im inneren Bereich gilt $H(f) = \cos^2(f \cdot T \cdot {\pi}/{ 2} ) .$
Anzumerken ist, dass die äquivalente Bandbreite $\Delta f = 1{\Delta t}$ betragen soll. Damit ist die äquivalente ${\Delta t}$ der Impulsantwort ebenfalls $T$ und man erhält:
- $$y(t) = T \cdot h(t) = {\rm si}(\pi \cdot {t}/{T} )\cdot \frac {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2}.$$
Zu beachten ist, dass das Ausgangssignal $y(t)$ im Gegensatz zur Impulsantwort $h(t)$ ohne Einheit ist. Durch Anwendung trigonomischer Umformungen kann dieses Signal auch wie folgt dargestellt werden: $$y(t) = {\pi}/{4} \cdot {\rm si}(\pi \cdot {t}/{T} )\cdot \left[ {\rm si}\left(\pi \cdot \left({t}/{T}+ 0.5 \right) \right)+ {\rm si}\left(\pi \cdot \left({t}/{T}- 0.5 \right) \right)\right].$$
Wählen Sie bei denolgenden Aufgaben die jeweils einfacher handhabbare Gleichung aus.
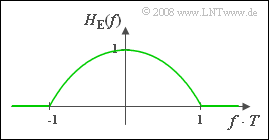
Für die Teilaufgabe (3) soll vorausgesetzt werden, dass das Signal $s(t)$ in der Mitte zwischen den beiden Frequenzgängen $H_{\rm S}(f)$ und $H_{\rm S}(f)$ ein Rechteckimpuls ist. Demzufolge muss gelten:
- $$H_{\rm E}(f) = {\rm si }(\pi f T ) .$$
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Einige systemtheoretische Tiefpassfunktionen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Sie können Ihre Ergebnisse mit dem Interaktionsmodul Frequenzgänge im Frequenz- und Zeitbereich überprüfen:
Fragebogen
Musterlösung
(2) Zur Berechnung dieser Signalwerte ist die zweite Darstellung besser geeignet:
$$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)\cdot \left[ {\rm
si}(\pi)+ {\rm si}(0)\right].$$
Mit si(0) = 1 und si(π) = 0 erhält man so: $$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)= {\pi}/{4} \cdot \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{ = 0.5}.$$
In analoger Weise ergibt sich für t = 1.5T:
- $$y(t = 1.5T) = {\pi}/{4} \cdot {\rm si}(3\pi/2)\cdot \left[ {\rm si}(2\pi)+ {\rm si}(\pi)\right] \hspace{0.15cm}\underline{ = 0}.$$
Hierbei ist ${\rm si}(\pi) = {\rm si}(\pi) = 0$ berücksichtigt. Zu den Zeitpunkten $t/T = 2.5, 3.5, ... $ gilt ebenfalls $y(t) = 0$, wie die folgende Grafik zeigt.
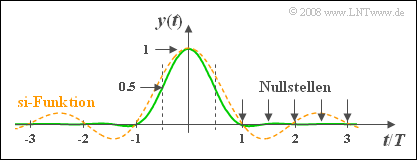
(3) Für große Werte von $t$ gilt näherungsweise (wenn man die „1” im Nenner vernachlässigt):
- $$y(t)= {\rm si}(\pi \cdot {t}/{T} )\cdot \frac {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2} \approx \frac {\sin(\pi \cdot t / T )\cdot \cos(\pi \cdot t / T )}{ - (\pi \cdot t/T )(2 \cdot t/T )^2} = - \frac {\sin(2\pi \cdot t / T )}{ 8 \pi \cdot( t/T )^3}.$$
Hierbei ist berücksichtigt, dass $\sin(\alpha) \cdot \cos(\alpha) = \sin(2\alpha)/2$ ist. Zum Zeitpunkt $t = 10.75 T$ gilt dann:
- $$\sin(2\pi \cdot t / T ) = \sin (21.5\pi)= \sin (1.5\pi) = -1.$$
- $$\Rightarrow \hspace{0.3cm} y(t = 10.75 T) = \frac {1 }{ 8 \pi \cdot( 10.75 )^3} \hspace{0.15cm}\underline{= 32} \cdot 10^{-6}.$$
(4) Der Empfängerfrequenzgang lautet für$|f \cdot T| \le 1$ : $$H_{\rm E}(f) = \frac{H(f)}{H_{\rm S}(f)}= \frac{\cos^2(\pi f T /2)}{{\rm si}(\pi fT)}.$$ Dieser Funktionsverlauf ist in der Grafik dargestellt. Für die gesuchten Stützwerte gilt: $$H_{\rm E}(f = 0) = \frac{\cos^2(0)}{{\rm si}(0)} \hspace{0.15cm}\underline{ = 1},$$ $$H_{\rm E}(f = {0.5}/T \hspace{-0.15cm} = \hspace{-0.15cm} \frac{\cos^2(\pi/4)}{{\rm si}(\pi/2)}= (\sqrt{2} / 2)^2 \cdot \frac{\pi}{2} = \hspace{-0.15cm} \frac{\pi}{4}\hspace{0.15cm}\underline{ \approx 0.785},$$ $$H_{\rm E}(f = {1}/{T}) = \frac{\cos^2(\pi/2)}{{\rm si}(\pi)} = "0/0"\hspace{0.15cm}\underline{= 0}.$$
Bei diesem Ergebnis ist berücksichtigt, dass im gesamten Frequenzbereich $H_{\rm S}(f) \ge H(f) $ gilt. Eigentlich müsste der zuletzt berechnete Wert durch einen Grenzübergang mathematisch-exakt bestimmt werden.