Aufgaben:Aufgabe 2.1: Linear? - Nichtlinear?: Unterschied zwischen den Versionen
| Zeile 61: | Zeile 61: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | ||
| − | + | '''(1)''' Aufgrund der Kennlinie mit linearem und quadratischem Anteil gilt: | |
| + | $$y(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) + {1 \, | ||
\rm V}^{\rm -1} \cdot ({2 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_0 | \rm V}^{\rm -1} \cdot ({2 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_0 | ||
| − | t ) | + | t ) = {2 \, \rm V} \cdot \left[ 1 + {\rm cos}(2\pi \cdot f_0 \cdot t |
| − | ) +{\rm cos}( | + | ) +{\rm cos}(2\pi \cdot 2f_0 \cdot t ) \right].$$ |
| + | |||
| + | Zum Zeitpunkt $t= 0$ tritt somit der <u>Signalwert 6 V</u> auf. | ||
| − | + | '''(2)''' Ein ideales System kommt wegen $z(t) ≠ x(t)$ nicht in Frage. Möglich sind die <u>Alternativen 2 und 3</u>. | |
| + | *Bei nur einer Eingangsfrequenz ($f_0 = 5 \ \rm kHz$) im Testsignal ist keine Aussage möglich, ob eine zweite Frequenzkomponente mit $f \ne f_0$ ebenfalls um $\alpha = 0.5$ gedämpft und um $\tau = T_0/4 = 50 \ \mu s$ verzögert würde. | ||
| + | *Ergäbe sich für die zweite Frequenzkomponente $\alpha = 0.5$ und $\tau = T_0/4 = 50 \ \mu s$, so würde ein ''verzerrungsfreies System'' vorliegen. | ||
| + | *Ergäbe sich für die zweite Frequenzkomponente $\alpha \ne 0.5$ und $\tau \ne T_0/4$, so wäre das System ''linear verzerrend''. | ||
| + | Die letzte Alternative müsste der Beobachter – obwohl teilweise zutreffend – logischerweise verneinen. | ||
| − | + | '''(3)''' Er würde erkennen, dass $S_2$ ein linear verzerrendes System ist ⇒ <u>Lösungsvorschlag 2</u>: | |
| + | Bei einem verzerrungsfreien System müsste $z(t)$ zusätzlich noch eine Gleichkomponente und eine $10 \ \rm kHz$-Komponente beinhalten, bei einem nichtlinear verzerrenden System noch größere Frequenzanteile (bei Vielfachen von $10 \ \rm kHz$). | ||
| − | + | '''(4)''' In diesem Fall würde gelten: | |
| + | $$y(t) = {2 \, \rm V} \cdot \left[ 1 + {\rm cos}(2\pi \cdot 10 \ {\rm kHz} \cdot t | ||
| + | ) +{\rm cos}(2\pi \cdot 20 \ {\rm kHz} \cdot t ) \right].$$ | ||
| + | Das heißt: $Y(f)$ würde Spektrallinien bei $f = 0$, $10 \ \rm kHz$ und $20 \ \rm kHz$ aufweisen. | ||
| − | + | Die auf der Angabenseite beschriebene Messung mit $f_0 = 5 \ \rm kHz$ hat aber gezeigt, dass $H_2(f = 0) = H_2(f = 10 \ {\rm kHz}) = 0$ gelten muss. Die einzig mögliche Signalform ist somit | |
| − | + | $$z(t) = {2 \, \rm V} \cdot H_2 (f = {20 \, \rm kHz})\cdot {\rm | |
cos}(2\pi \cdot {20 \, \rm kHz} \cdot t ) .$$ | cos}(2\pi \cdot {20 \, \rm kHz} \cdot t ) .$$ | ||
| − | + | Möglich sind also die <u>Lösungsvorschläge 1 und 3</u>, je nachdem, ob das System $S_2$ die Frequenz $20 \ {\rm kHz}$ unterdrückt oder durchlässt. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 1. Februar 2017, 11:29 Uhr
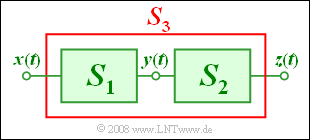
Wir betrachten die skizzierte Anordnung mit Eingangssignal $x(t)$ und Ausgangssignal $z(t)$:
- Das System $S_1$ ist durch folgende Gleichung beschreibbar:
- $$y(t) = x(t) + {1 \, \rm V}^{\rm -1} \cdot x^2(t) .$$
- Über das System $S_2$ mit Eingangssignal $y(t)$ und Ausgangssignal $z(t)$ ist nichts weiter bekannt.
- Das System $S_3$ ist die Zusammenschaltung von $S_1$ und $S_2$.
An den Eingang wird eine Schwingung mit $f_0 = 5 \ \rm kHz$ angelegt:
- $$x(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) .$$
Damit erhält man am Ausgang des Gesamtsystems $S_3$:
- $$z(t) = {1 \, \rm V} \cdot {\rm sin}(2\pi f_0 t ) .$$
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Klassifizierung der Verzerrungen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Gegeben ist die folgende trigonometrische Beziehung:
- $$\cos^2(\alpha) = {1}/{2} \cdot \left[ 1 + \cos(2\alpha)\right].$$
Fragebogen
Musterlösung
(1) Aufgrund der Kennlinie mit linearem und quadratischem Anteil gilt: $$y(t) = {2 \, \rm V} \cdot {\rm cos}(2\pi f_0 t ) + {1 \, \rm V}^{\rm -1} \cdot ({2 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_0 t ) = {2 \, \rm V} \cdot \left[ 1 + {\rm cos}(2\pi \cdot f_0 \cdot t ) +{\rm cos}(2\pi \cdot 2f_0 \cdot t ) \right].$$
Zum Zeitpunkt $t= 0$ tritt somit der Signalwert 6 V auf.
(2) Ein ideales System kommt wegen $z(t) ≠ x(t)$ nicht in Frage. Möglich sind die Alternativen 2 und 3.
- Bei nur einer Eingangsfrequenz ($f_0 = 5 \ \rm kHz$) im Testsignal ist keine Aussage möglich, ob eine zweite Frequenzkomponente mit $f \ne f_0$ ebenfalls um $\alpha = 0.5$ gedämpft und um $\tau = T_0/4 = 50 \ \mu s$ verzögert würde.
- Ergäbe sich für die zweite Frequenzkomponente $\alpha = 0.5$ und $\tau = T_0/4 = 50 \ \mu s$, so würde ein verzerrungsfreies System vorliegen.
- Ergäbe sich für die zweite Frequenzkomponente $\alpha \ne 0.5$ und $\tau \ne T_0/4$, so wäre das System linear verzerrend.
Die letzte Alternative müsste der Beobachter – obwohl teilweise zutreffend – logischerweise verneinen.
(3) Er würde erkennen, dass $S_2$ ein linear verzerrendes System ist ⇒ Lösungsvorschlag 2: Bei einem verzerrungsfreien System müsste $z(t)$ zusätzlich noch eine Gleichkomponente und eine $10 \ \rm kHz$-Komponente beinhalten, bei einem nichtlinear verzerrenden System noch größere Frequenzanteile (bei Vielfachen von $10 \ \rm kHz$).
(4) In diesem Fall würde gelten: $$y(t) = {2 \, \rm V} \cdot \left[ 1 + {\rm cos}(2\pi \cdot 10 \ {\rm kHz} \cdot t ) +{\rm cos}(2\pi \cdot 20 \ {\rm kHz} \cdot t ) \right].$$ Das heißt: $Y(f)$ würde Spektrallinien bei $f = 0$, $10 \ \rm kHz$ und $20 \ \rm kHz$ aufweisen.
Die auf der Angabenseite beschriebene Messung mit $f_0 = 5 \ \rm kHz$ hat aber gezeigt, dass $H_2(f = 0) = H_2(f = 10 \ {\rm kHz}) = 0$ gelten muss. Die einzig mögliche Signalform ist somit $$z(t) = {2 \, \rm V} \cdot H_2 (f = {20 \, \rm kHz})\cdot {\rm cos}(2\pi \cdot {20 \, \rm kHz} \cdot t ) .$$
Möglich sind also die Lösungsvorschläge 1 und 3, je nachdem, ob das System $S_2$ die Frequenz $20 \ {\rm kHz}$ unterdrückt oder durchlässt.