Aufgaben:Aufgabe 2.4: Klirrfaktor und Verzerrungsleistung

• Zurück zum Buch

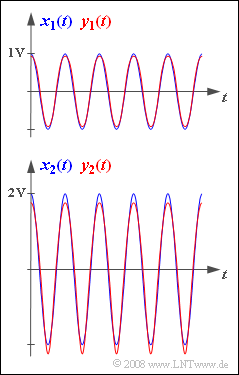
Zum Test eines Nachrichtenübertragungssystems wird an seinen Eingang ein Cosinussignal $$x_1(t) = A_x \cdot \cos(\omega_0 t)$$

mit der Amplitude $A_x = 1 \ \rm V$ angelegt. Am Systemausgang tritt dann das folgende Signal auf: $$y_1(t) = {0.992 \,\rm V} \cdot \cos(\omega_0 t) - {0.062 \,\rm V} \cdot \cos(2\omega_0 t)+ \hspace{0.05cm}...$$

• In der oberen Grafik sind die Signale $x_1(t)$ und $y_1(t)$ dargestellt. Oberwellen mit Amplituden kleiner als $10 \ \rm mV$ sind hierbei nicht berücksichtigt.
• Das untere Bild zeigt das Eingangssignal $x_2(t)$ mit der Ampiltude $A_x = 2 \ \rm V$ sowie das dazugehörige Ausgangssignal, wiederum ohne Oberwellen kleiner als $10 \ \rm mV$:

$$y_2(t) = {1.938 \,\rm V} \cdot \cos(\omega_0 t) - {0.234 \,\rm V} \cdot \cos(2\omega_0 t) + {0.058 \,\rm V} \cdot \cos(3\omega_0 t) -{0.018 \,\rm V} \cdot \cos(4\omega_0 t) + \hspace{0.05cm}...$$

Es ist offensichtlich, dass der Index „1” bzw. „2” jeweils die normierte Amplitude des Eingangssignals kennzeichnet.

Dieses System soll anhand des im Quantitatives Maß für die Signalverzerrungen definierten Signal–zu–Verzerrungs–Leistungsverhältnisses $$\rho_{\rm V} = { P_{x}}/{P_{\rm V}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot \lg \hspace{0.1cm}\rho_{\rm V} = 10 \cdot \lg \hspace{0.1cm}{ P_{x}}/{P_{\rm V}}\hspace{0.3cm} \left( {\rm in \hspace{0.15cm} dB} \right)$$

sowie des Klirrfaktors $K$ analysiert werden:

• $P_x$ bezeichnet die Leistung des Eingangssignals,
• die so genannte Verzerrungsleistung $P_{\rm V}$ gibt jeweils die Leistung (den quadratischen Mittelwert) des Differenzsignals $\varepsilon(t) = y(t) - x(t)$ an.

Zur Bestimmung dieser Leistungen muss jeweils über die quadrierten Signale gemittelt werden. Einfacher ist in dieser Aufgabe jedoch die Leistungsberechnung im Frequenzbereich.

Hinweise:

• Die Aufgabe gehört zum Kapitel Nichtlineare Verzerrungen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Alle hier abgefragten Leistungen beziehen sich auf den Widerstand $R = 1 \ \rm \Omega$ und haben somit die Einheit ${\rm V}^2$

Fragebogen

1

Berechnen Sie den Klirrfaktor $K$ für die Eingangsamplitude $A_x = 1\ \rm V$.

$A_x = 1\ \rm V$:  $ K \ =$ $\%$

2

WelcherKlirrfaktor ergibt sich mit der Eingangsamplitude $A_x = 2\ \rm V$?

$A_x = 2\ \rm V$:  $ K \ =$ $\%$

3

Welche Aussagen sind für die Signale $x_2(t)$ und $y_2(t)$ zutreffend?

	Die untere Halbwelle verläuft spitzförmiger als die obere.
	Der Maximal– und Minimalwert von $y_2(t)$ sind unsymmetrisch zu $0$.
	Bei anderer Frequenz würde sich ein anderer Klirrfaktor ergeben.

4

Wie groß ist die Leistung $P_x$ des Eingangssignals $x_2(t)$ in ${\rm V}^2$, also umgerechnet auf den Bezugswiderstand $R = 1 \ \rm \Omega$?

$P_x \ =$ $\ {\rm V}^2$

5

Wie groß ist die „Leistung” $P_{\rm V}$ des Differenzsignals $\varepsilon_2(t)$? Hinweis: $P_{\rm V}$ wird in diesem Tutorial auch als „Verzerrungsleistung” bezeichnet.

$P_{\rm V} \ =$ $\ {\rm V}^2$

6

Wie groß ist das Signal–zu–Verzerrungs–Leistungsverhältnis in ${\rm dB}$?

$10 \cdot {\rm lg} \ \rho_{\rm V} \ = $ $\ {\rm dB}$

7

Welche der folgenden Aussagen treffen bei cosinusförmigem Eingangssignal zu?

	Der Klirrfaktor kann allein aus den Koeffizienten $A_1$, $A_2$, $A_3$, ... der Ausgangsgröße berechnet werden.
	Das Signal–zu–Verzerrungs–Leistungsverhältnis $10 \cdot {\rm lg} \ \rho_{\rm V}$ ist allein aus den Koeffizienten $A_1$, $A_2$, $A_3$, ... der Ausgangsgröße berechenbar.
	Für den Sonderfall $A_1 = A_x$  ⇒  keine Veränderung der Grundwelle   können $\rho_{\rm V}$ und $K$ direkt ineinander umgerechnet werden.

Musterlösung

Musterlösung

(1)  Mit der Eingangsamplitude $A_x = 1 \ \rm V$ entsprechend der oberen Skizze liefert nur der Klirrfaktor zweiter Ordnung einen relevanten Beitrag. Deshalb gilt: $$K \approx K_2 = \frac{0.062 \,\,{\rm V}}{0.992 \,\,{\rm V}} \hspace{0.15cm}\underline{\approx 6.25 \%}.$$

(2)  Für die Eingangsamplitude $A_x = 2 \ \rm V$ (untere Skizze) lauten die verschiedenen Klirrfaktoren: $$K_2 = \frac{0.234 \,\,{\rm V}}{1.938 \,\,{\rm V}} \approx 0.121, \hspace{0.5cm} K_3 = \frac{0.058 \,\,{\rm V}}{1.938 \,\,{\rm V}} \approx 0.030, \hspace{0.5cm}K_4 = \frac{0.018 \,\,{\rm V}}{1.938 \,\,{\rm V}} \approx 0.009.$$

Somit lautet der Gesamtklirrfaktor: $$K = \sqrt{K_2^2 + K_3^2 + K_4^2 + ... }\hspace{0.15cm}\underline{ \approx 12.5 \%}.$$

(3)  Richtig sind hier die beiden ersten Lösungsvorschläge:

• Hier bewirken die nichtlinearen Verzerrungen, dass die untere Halbwelle spitzförmiger verläuft als die obere. Da zudem $y(t)$ gleichsignalfrei ist, gilt $y_{\rm max} = 1.75 \ \rm V$ und $y_{\rm min} = -2.25 \ \rm V$. Die Symmetrie bezüglich der Nulllinie ist somit nicht mehr gegeben.
• Bei einem nichtlinearen System ist der Klirrfaktor $K$ unabhängig von der Frequenz des cosinusförmigen Eingangssignals, aber stark abhängig von dessen Amplitude.

(4)  Der Effektivwert eines Cosinussignals ist bekanntlich das $\sqrt{0.5}$–fache der Amplitude. Das Quadrat hiervon bezeichnet man als die Leistung: $$P_x = \frac{A_x^2}{2} = \frac{(2 \,{\rm V})^2}{2}\hspace{0.15cm}\underline{ = 2\,{\rm V^2}}.$$

Eigentlich hängt die Leistung ja auch vom Bezugswiderstand $R$ ab und besitzt die Einheit „Watt”. Mit $R = 1 \ \rm \Omega$ ergibt sich $P_x = 2 \ \rm W$, also der geanau gleiche Zahlenwert wie bei dieser einfacheren Berechnung.

(5)  Bezeichnet man mit $A_1$ die Amplitude der Grundwelle von $y_2(t)$ und mit $A_2$, $A_3$ und $A_4$ die so genannten Oberwellen, so erhält man für die Verzerrungsleistung durch Berechnung im Frequenzbereich: $$P_{\rm V} = \frac{1}{2} \cdot \left[ (A_1 - A_x)^2 + A_2^2+ A_3^2+ A_4^2\right] = \frac{1}{2} \cdot \left[ (-2 \,{\rm V} \hspace{-0.05cm}+ \hspace{-0.05cm}1.938 \,{\rm V} )^2 \hspace{-0.05cm}+ \hspace{-0.05cm} (0.234 \,{\rm V})^2 \hspace{-0.05cm}+ \hspace{-0.05cm} (0.058 \,{\rm V})^2 \hspace{-0.05cm}+ \hspace{-0.05cm} (0.018 \,{\rm V})^2 \right] \hspace{0.15cm}\underline{\approx 0.031 \,{\rm V}^2}.$$

Hierbei bezeichnet $A_x$ die Amplitude des Eingangssignals. Die Vorzeichen der Oberwellen spielen bei dieser Berechnung keine Rolle.

(6)  Mit den Ergebnissen der Unterpunkte (4) und (5) erhält man: $$10 \cdot \lg \rho_{V} = 10 \cdot \lg \frac{P_x}{P_{\rm V}}= 10 \cdot \lg \frac{2.000\,{\rm V^2}}{0.031 \,{\rm V}^2} \hspace{0.15cm}\underline{\approx 18.10 \,{\rm dB}}.$$

(7)  Die erste Aussage ist richtig, denn es gilt:

$$K^2 = \frac{A_2^2 + A_3^2 + A_4^2 + ... }{A_1^2}.$$

Dagegen gilt für den Kehrwert des Signal–zu–Verzerrungs–Leistungsverhältnisses: $${1}/{\rho_{\rm V}} = \frac{(A_1 - A_x)^2+A_2^2 + A_3^2 + A_4^2 + ... }{A_x^2}.$$

Bei der Berechnung der Verzerrungsleistung $P_{\rm V}$ wird auch eine Verfälschung der Grundwellenamplitude (diese ist nun $A_1$ anstelle von $A_x$ berücksichtigt. Außerdem wird die Verzerrungsleistung nicht auf $A_1^2$, sondern auf $A_x^2$ bezogen.

Allgemein gilt zwischen dem Signal–zu–Verzerrungs–Leistungsverhältnis und dem Klirrfaktor folgender Zusammenhang: $${\rho_{\rm V}} = \frac{A_x^2}{(A_1 - A_x)^2 + K^2 \cdot A_1^2}.$$

Mit $A_1 = A_x$ vereinfacht sich diese Gleichung wie folgt:

$${\rho_{\rm V}} = {1}/{ K^2 }.$$

Anmerkungen:

• Ein Klirrfaktor von $1\%$ entspricht in diesem Fall dem Ergebnis $10 \cdot \lg \rho_{V} = 40 \,{\rm dB}$.
• Mit dem Klirrfaktor $K = 0.125$ aus Teilaufgabe /2) hätte man mit der Näherung $A_1 \approx A_x$ sofort $10 \cdot \lg \rho_{\rm V} = 18.06 \,{\rm dB}$ erhalten.
• Der unter Punkt (7) errechnete tatsächliche Wert ($18.10 \ \rm dB$) weicht hiervon nicht all zu sehr ab.

Richtig sind also die Lösungsvorschläge 1 und 3.