Aufgaben:Aufgabe 3.3: p-Übertragungsfunktion

• Zurück zum Buch

Jedes lineare zeitinvariante System, das durch eine Schaltung aus diskreten zeitkonstanten Bauelementen (Widerstände $R$, Kapazitäten $C$, Induktivitäten $L$, Verstärkerelemente, usw.) realisiert werden kann, ist kausal und besitzt zudem eine gebrochen–rationale p–Übertragungsfunktion der Form

$$H_{\rm L}(p)= \frac {A_Z \cdot p^Z + ... + A_1 \cdot p + A_0} {B_N \cdot p^N + ... + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$

Alle Koeffizienten $A_Z$, ... , $A_0$, $B_N$, ... , $B_0$ sind reell. $Z$ bezeichnet den Grad des Zählerpolynoms $Z(p)$ und $N$ den Grad des Nennerpolynoms $N(p)$. Eine äquivalente Darstellungsform obiger Gleichung lautet:

$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i}} {\prod\limits_{i=1}^N p - p_{\rm x i}}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot ... \cdot (p - p_{{\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot ... \cdot (p - p_{{\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$

Die $Z + N + 1$ Parameter bedeuten:

• $K = A_Z/B_n$ ist ein konstanter Faktor. Gilt $Z = N$, so ist dieser dimensionslos.
• Die Lösungen der Gleichung $Z(p) = 0$ ergeben die $Z$ Nullstellen $p_{{\rm o}1}$, ... , $p_{{\rm o}N}$ von $H_{\rm L}(p)$.
• Die Nullstellen des Nennerpolynoms $N(p)$ ergeben die $N$ Polstellen $p_{{\rm x}1}$, ... , $p_{{\rm x}N}$ der Übertragungsfunktion.

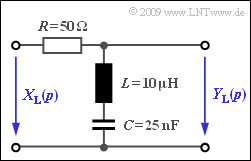
Diese Kenngrößen sollen für die in der Grafik gezeigten Schaltung mit den Bauelementen

$$R = 50\,\,{\rm \Omega}\hspace{0.05cm},\hspace{0.2cm} L = 10\,\,{\rm \mu H}\hspace{0.05cm},\hspace{0.2cm}C = 25\,\,{\rm nF}$$

ermittelt werden. Außerdem soll der Frequenzgang $H(f)$ nach Fourier bestimmt werden, der sich aus $H_{\rm L}(p)$ durch die Substitution $p= {\rm j } \cdot 2\pi f$ ergibt.

Hinweise:

• Die Aufgabe gehört zum Kapitel Laplace–Transformation und p–Übertragungsfunktion.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Als Hilfsgrößen werden in dieser Aufgabe verwendet:

$$A = \frac{R}{2L}\hspace{0.05cm},\hspace{0.2cm} B = \frac{1}{\sqrt{LC}}\hspace{0.05cm} .$$

Fragebogen

1

Ermitteln Sie die $p$–Übertragungsfunktion. Welche asymptotischen Werte erhält man für $p → 0$ und $p → \infty$?

$H_L(p → 0) \ =$

$H_L(p → ∞) \ =$

2

Ermitteln Sie aus $H_{\rm L}(p)$ den Frequenzgang $H(f)$, indem Sie $p= {\rm j } \cdot 2\pi f$ setzen. Welche der folgenden Aussagen treffen zu?

	Es handelt sich um einen Bandpass.
	Es handelt sich um eine Bandsperre.
	Ohne genaue Kenntnis von $R$, $L$ und $C$ ist keine Aussage möglich.

3

Berechnen Sie die Hilfsgrößen $A$ und $B$ für $R = 50 \ \rm \Omega$, $L = 10 \ μ\rm H$, $C = 25 \ \rm nF$.

$A \ =$ $\cdot \ 10^6 \ \rm 1/s$

$B \ =$ $\cdot \ 10^6 \ \rm 1/s$

4

Stellen Sie $H_{\rm L}(p)$ in Pol–Nullstellen–Form dar. Wieviele Nullstellen ($Z$) und Pole ($N$) gibt es? Wie groß ist der konstante Faktor $K$?

$Z \ =$

$N \ =$

$K \ =$

5

Berechnen Sie die Nullstellen $p_\text{o1}$ und $p_\text{o1}$. Beachten Sie die Einheit&; $\rm 1/μs$.

obere Halbebene:    ${\rm Re}\{p_\text{o1}\} \ =$ $\ \rm 1/ \mu s$

${\rm Im}\{p_\text{o1}\} \ =$ $\ \rm 1/ \mu s$

untere Halbebene:    ${\rm Re}\{p_\text{o2}\} \ =$ $\ \rm 1/ \mu s$

${\rm Re}\{p_\text{o2}\} \ =$ $\ \rm1/ \mu s$

6

Berechnen Sie die Pole $p_\text{x1}$ und $p_\text{x2}$. Es gelte $|p_\text{x2}| > p_\text{x1}$|.

${\rm Re}\{p_\text{x1}\} \ =$ $\ \rm 1/ \mu s$

${\rm Im}\{p_\text{x1}\} \ =$ $\ \rm 1/ \mu s$

${\rm Re}\{p_\text{x2}\} \ =$ $\ \rm 1/ \mu s$

${\rm Im}\{p_\text{x2}\} \ =$ $\ \rm 1/ \mu s$

7

Wie kann man ohne Änderung der Nullstellen die Lage der Pole verändern?

	Änderung von R. L und C gleichbleibend.
	Änderung von L. R und C gleichbleibend.
	Änderung von C. L und R gleichbleibend.

8

Wie muss die Hilfsgröße A verändert werden (B gleichbleibend), damit eine doppelte Polstelle auftritt (aperiodischer Grenzfall)? Achtung: mit Einheit 1/μs.

$A$ = $\cdot 10^6\ 1/s$

Musterlösung

Musterlösung

1.  Nach dem Spannungsteilerprinzip kann für die p–Übertragungsfunktion geschrieben werden:

$$H_{\rm L}(p)= \frac {pL +{1}/{(pC)}} {R + pL + {1}/{(pC)}}= \frac { p^2 \cdot{LC}+1} {p^2 \cdot{LC} + p \cdot{RC}+ 1} \hspace{0.05cm} .$$

Die beiden gewünschten Grenzübergänge ergeben sich zu

$$\underline {H_{\rm L}(p \rightarrow 0)= 1, \hspace{0.2cm}H_{\rm L}(p \rightarrow \infty)= 1} \hspace{0.05cm} .$$

Daraus folgt, dass es sich weder um einen Tiefpass noch um einen Hochpass handeln kann. Sowohl bei sehr niedrigen als auch bei sehr hohen Frequenzen gilt y(t) = x(t).

2.  Ersetzt man p durch j · 2πf, so erhält man

$$H(f)= \frac {1 - (2\pi f)^2 \cdot LC} {1 - (2\pi f)^2 \cdot LC + {\rm j} \cdot 2\pi f \cdot RC} \hspace{0.05cm} .$$

Es gibt also stets eine Frequenz, bei der der Zähler 0 ist, nämlich die Resonanzfrequenz von L und C. Für diese Frequenz f₀ = 1 MHz/2π wirkt die Reihenschaltung von L und C wie ein Kurzschluss. Daraus folgt: Unabhängig von den Werten von R, L und C handelt es sich um eine Bandsperre (Lösungsvorschlag 2).

3.  Entsprechend dem Angabenblatt gilt:

$$A = \frac{R}{2L}= \frac{50\,{\rm \Omega}}{2 \cdot 10\,{\rm \mu H}} = \frac{50\,{\rm \Omega}}{2 \cdot 10^{-5 }\,{\rm \Omega s}}\hspace{0.15cm} \underline {= 2.5 \cdot 10^6 \, \,{1}/{\rm s}}\hspace{0.05cm},\\ B = \frac{1}{\sqrt{LC}} = \frac{1}{\sqrt{10^{-5 }\,{\rm \Omega s} \cdot 25 \cdot 10^{-9 }\,{\rm s/\Omega }}}\hspace{0.15cm} \underline {= 2 \cdot 10^6 \, \,{1}/{\rm s}}\hspace{0.05cm} .$$

4.  Mit A = R/(2L) und B² = 1/(LC) erhält man aus der in (a) ermittelten p–Übertragungsfunktion:

$$H_{\rm L}(p)= \frac { p^2 + {1}/(LC)} {p^2 + p \cdot{R}/{L} +{1}/(LC)} = \frac { p^2 + B^2} {p^2 + 2A \cdot p + B^2} \hspace{0.05cm} .$$

Das Zählerpolynom Z(p) und das Nennerpolynom N(p) sind jeweils quadratisch ⇒ Z = N = 2. Der konstante Faktor ergibt sich hier zu K = 1.

5.  Die Lösung der Gleichung p² + B² = 0 führt zum Ergebnis p = ± j · B und damit zu den Nullstellen

$${\rm Re}\{ p_{\rm o1}\} \underline {= 0}\hspace{-0.3cm} \hspace{1cm}{\rm Im}\{ p_{\rm o1}\} = 2.5 \cdot 10^6 \, \frac{1}{{\rm s}} \hspace{0.15cm} \underline { = 2.5}\,\, \frac{1}{\rm \mu s}\hspace{0.05cm},\\ {\rm Re}\{ p_{\rm o2}\}\hspace{0.15cm} \underline { = 0}\hspace{-0.3cm} \hspace{1cm}{\rm Im}\{ p_{\rm o2}\} =- 2.5 \cdot 10^6 \, \frac{1}{{\rm s}} \hspace{0.15cm} \underline { = - 2.5}\,\, \frac{1}{\rm \mu s}\hspace{0.05cm}.$$

Die Normierung der Frequenzvariablen p und aller Pole und Nullstellen auf die Einheit (μs)^–1 vereinfacht die numerische Auswertung, insbesondere im Zeitbereich. Verzichtet man auf die Einheit ganz, so ergeben sich alle t–Werte in Mikrosekunden.

6.  Setzt man das Nennerpolynom N(p) gleich 0, so ergibt sich folgende Bestimmungsgleichung:

$$p^2 + 2A \cdot p + B^2 = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x1,\hspace{0.05cm}2}= -A \pm \sqrt{A^2 - B^2} \hspace{0.05cm},$$

$${\rm Mit}\hspace{0.2cm}A = 2.5 \cdot 10^6 \, \frac{1}{\rm s}\hspace{0.05cm},\hspace{0.2cm} \sqrt{A^2 - B^2}= 1.5 \cdot 10^6 \, \frac{1}{{\rm s}}\hspace{0.05cm}:$$

$${\rm Re}\{ p_{\rm x1}\} = -1 \cdot 10^6 \, \frac{1}{{\rm s}}\hspace{0.15cm} \underline {= -1} \, \frac{1}{{\rm \mu s}}\hspace{-0.3cm} , \hspace{0.2cm}{\rm Im}\{ p_{\rm x1}\}\hspace{0.15cm} \underline { = 0} \hspace{0.05cm},\\ {\rm Re}\{ p_{\rm x2}\} = -4 \cdot 10^6 \, \frac{1}{{\rm s}}\hspace{0.15cm} \underline {= -4} \, \frac{1}{{\rm \mu s}}\hspace{-0.3cm} , \hspace{0.2cm}{\rm Im}\{ p_{\rm x2}\}\hspace{0.15cm} \underline { = 0} \hspace{0.05cm}.$$

Dieses Ergebnis ist nur eindeutig unter Berücksichtigung der Angabe |p_x2| > |p_x1|.

7.  Da man nur eines der Bauelemente ändern soll, müssen L und C gleich bleiben, da sonst auch die Nullstellen verschoben würden  ⇒  man muss den Widerstandswert R ändern  ⇒ Antwort 1.

8.  Entsprechend dem Ergebnis aus (7) ergibt sich eine doppelte Polstelle für A = B = 2 · 10⁶ 1/s. Dazu muss der Ohmsche Widerstand von 50 Ω auf 40 Ω herabgesetzt werden. Der doppelte Pol liegt dann bei –2 · 10⁶ 1/s. Oder bei anderer Normierung bei –2 (μs)^–1.