Aufgaben:Aufgabe 4.15: WDF und Kovarianzmatrix: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID669__Sto_A_4_15.png |right|]] | + | [[Datei:P_ID669__Sto_A_4_15.png |right|Gegebene Korrelationsmatrizen]] |
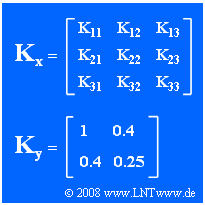
| − | + | Wir betrachten hier die dreidimensionale Zufallsgröße $\mathbf{x}$, deren allgemein dargestellte Kovarianzmatrix $\mathbf{K}(\mathbf{x})$ in der Grafik angegeben ist. Die Zufallsgröße besitzt folgende Eigenschaften: | |
| − | + | * Die drei Komponenten sind gaußverteilt und es gilt für die Elemente der Kovarianzmatrix: | |
:$$K_{ij} = \sigma_i \cdot \sigma_j \cdot \rho_{ij}.$$ | :$$K_{ij} = \sigma_i \cdot \sigma_j \cdot \rho_{ij}.$$ | ||
| − | + | * Die Elemente auf der Hauptdiagonalen seien bekannt: | |
| − | |||
:$$ K_{11} =1, K_{22} =0, K_{33} =0.25.$$ | :$$ K_{11} =1, K_{22} =0, K_{33} =0.25.$$ | ||
| + | * Der Korrelationskoeffizient zwischen den Koeffizienten $x_1$ und $x_3$ beträgt $0.8$. | ||
| − | + | Im zweiten Teil der Aufgabe soll die Zufallsgröße $\mathbf{y}$ mit den beiden Komponenten $y_1$ und $y_2$ betrachtet werden, deren Kovarianzmatrix $\mathbf{K}(\mathbf{y})$ durch die angegebenen Zahlenwerte $(1, 0.4, 0.25)$ bestimmt ist. | |
| − | |||
| − | |||
| − | + | Die Wahrscheinlichkeitsdichtefunktion einer mittelwertfreien Gaußschen zweidimensionalen Zufallsgröße $\mathbf{y}$ lautet gemäß den Angaben auf der Seite [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgrößen#Zusammenhang_zwischen_Kovarianzmatrix_und_WDF|Zusammenhang zwischen Kovarianzmatrix und WDF]] mit $N = 2$: | |
:$$\mathbf{f_y}(\mathbf{y}) = \frac{1}{{(2 \pi) \cdot | :$$\mathbf{f_y}(\mathbf{y}) = \frac{1}{{(2 \pi) \cdot | ||
| − | \sqrt{|\mathbf{K_y}|}}}\cdot {\rm exp}{\left(-\frac{1}{2}\cdot \mathbf{y} ^{\rm T}\cdot\mathbf{K_y}^{-1} \cdot \mathbf{y} \right)}= | + | \sqrt{|\mathbf{K_y}|}}}\cdot {\rm exp}{\left(-\frac{1}{2}\cdot \mathbf{y} ^{\rm T}\cdot\mathbf{K_y}^{-1} \cdot \mathbf{y} \right)}= C \cdot {\rm exp}{\left(-\gamma_1 \cdot y_1^2 + \gamma_2 \cdot y_2^2 +\gamma_{12} \cdot y_1 \cdot y_2 \right)}.$$ |
| − | + | In den Teilaufgaben (5) und (6) sollen der Vorfaktor $C$ und die weiteren WDF-Koeffizienten $\&gamma_1$, $\&gamma_2$ und $\&gamma_{12}$ gemäß dieser Vektordarstellung berechnet werden. Dagegen würde die entsprechende Gleichung bei herkömmlicher Vorgehensweise entsprechend dem Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen#Wahrscheinlichkeitsdichte-_und_Verteilungsfunktion|Zweidimensionale Gaußsche Zufallsgrößen]] lauten: | |
:$$f_{y_1,\hspace{0.1cm}y_2}(y_1,y_2)=\frac{\rm 1}{\rm 2\pi \sigma_1 | :$$f_{y_1,\hspace{0.1cm}y_2}(y_1,y_2)=\frac{\rm 1}{\rm 2\pi \sigma_1 | ||
\sigma_2 \sqrt{\rm 1-\rho^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 | \sigma_2 \sqrt{\rm 1-\rho^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 | ||
| Zeile 27: | Zeile 25: | ||
y}_1{\it y}_2}{\sigma_1 \cdot \sigma_2}) \rm \Bigg].$$ | y}_1{\it y}_2}{\sigma_1 \cdot \sigma_2}) \rm \Bigg].$$ | ||
| − | : | + | |
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgrößen|Verallgemeinerung auf N-dimensionale Zufallsgrößen]]. | ||
| + | *Einige Grundlagen zur Anwendung von Vektoren und Matrizen finden sich auf den Seiten [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgrößen#Grundlagen_der_Matrizenrechnung:_Determinante_einer_Matrix|Determinante einer Matrix]] sowie [[Stochastische_Signaltheorie/Verallgemeinerung_auf_N-dimensionale_Zufallsgrößen#Grundlagen_der_Matrizenrechnung:_Inverse_einer_Matrix|Inverse einer Matrix]] | ||
| + | *Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Zweidimensionale_Gaußsche_Zufallsgrößen|Zweidimensionale Gaußsche Zufallsgrößen]]. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
Version vom 3. April 2017, 09:17 Uhr
Wir betrachten hier die dreidimensionale Zufallsgröße $\mathbf{x}$, deren allgemein dargestellte Kovarianzmatrix $\mathbf{K}(\mathbf{x})$ in der Grafik angegeben ist. Die Zufallsgröße besitzt folgende Eigenschaften:
- Die drei Komponenten sind gaußverteilt und es gilt für die Elemente der Kovarianzmatrix:
- $$K_{ij} = \sigma_i \cdot \sigma_j \cdot \rho_{ij}.$$
- Die Elemente auf der Hauptdiagonalen seien bekannt:
- $$ K_{11} =1, K_{22} =0, K_{33} =0.25.$$
- Der Korrelationskoeffizient zwischen den Koeffizienten $x_1$ und $x_3$ beträgt $0.8$.
Im zweiten Teil der Aufgabe soll die Zufallsgröße $\mathbf{y}$ mit den beiden Komponenten $y_1$ und $y_2$ betrachtet werden, deren Kovarianzmatrix $\mathbf{K}(\mathbf{y})$ durch die angegebenen Zahlenwerte $(1, 0.4, 0.25)$ bestimmt ist.
Die Wahrscheinlichkeitsdichtefunktion einer mittelwertfreien Gaußschen zweidimensionalen Zufallsgröße $\mathbf{y}$ lautet gemäß den Angaben auf der Seite Zusammenhang zwischen Kovarianzmatrix und WDF mit $N = 2$:
- $$\mathbf{f_y}(\mathbf{y}) = \frac{1}{{(2 \pi) \cdot \sqrt{|\mathbf{K_y}|}}}\cdot {\rm exp}{\left(-\frac{1}{2}\cdot \mathbf{y} ^{\rm T}\cdot\mathbf{K_y}^{-1} \cdot \mathbf{y} \right)}= C \cdot {\rm exp}{\left(-\gamma_1 \cdot y_1^2 + \gamma_2 \cdot y_2^2 +\gamma_{12} \cdot y_1 \cdot y_2 \right)}.$$
In den Teilaufgaben (5) und (6) sollen der Vorfaktor $C$ und die weiteren WDF-Koeffizienten $\&gamma_1$, $\&gamma_2$ und $\&gamma_{12}$ gemäß dieser Vektordarstellung berechnet werden. Dagegen würde die entsprechende Gleichung bei herkömmlicher Vorgehensweise entsprechend dem Kapitel Zweidimensionale Gaußsche Zufallsgrößen lauten:
- $$f_{y_1,\hspace{0.1cm}y_2}(y_1,y_2)=\frac{\rm 1}{\rm 2\pi \sigma_1 \sigma_2 \sqrt{\rm 1-\rho^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 (1-\rho^{\rm 2})}\cdot(\frac { y_1^{\rm 2}}{\sigma_1^{\rm 2}}+\frac { y_2^{\rm 2}}{\sigma_2^{\rm 2}}-\rm 2\rho \frac{{\it y}_1{\it y}_2}{\sigma_1 \cdot \sigma_2}) \rm \Bigg].$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Verallgemeinerung auf N-dimensionale Zufallsgrößen.
- Einige Grundlagen zur Anwendung von Vektoren und Matrizen finden sich auf den Seiten Determinante einer Matrix sowie Inverse einer Matrix
- Bezug genommen wird auch auf das Kapitel Zweidimensionale Gaußsche Zufallsgrößen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- 1. Anhand der Kovarianzmatrix Kx ist keine Aussage darüber möglich, ob die zugrunde liegende Zufallsgröße x mittelwertfrei oder mittelwertbehaftet ist, da ein eventueller Mittelwert m herausgerechnet wird. Um Aussagen über den Mittelwert machen zu können, müsste die Korrelationsmatrix Rx bekannt sein. Aus K22 = (σ2)2 = 0 folgt zwingend, dass alle Elemente in der zweiten Zeile (K21, K23) und der zweiten Spalte (K12, K32) ebenfalls 0 sind. Dagegen ist die dritte Aussage falsch: Die Elemente sind symmetrisch zur Hauptdiagonalen, so dass stets K31 = K13 gelten muss. Richtig ist nur der Vorschlag 2.
- 2. Aus K11 = 1 und K33 = 0.25 folgen direkt σ1 = 1 und σ3 = 0.5. Zusammen mit dem Korrelationskoeffizienten ρ13 = 0.8 (siehe Angabenblatt) erhält man somit:
- $$K_{13} = K_{31} = \sigma_1 \cdot \sigma_2 \cdot \rho_{13}\hspace{0.15cm}\underline{= 0.4}.$$
- 3. Die Determinante der Matrix Ky lautet:
- $$|{\mathbf{K_y}}| = 1 \cdot 0.25 - 0.4 \cdot 0.4 \hspace{0.15cm}\underline{= 0.09}.$$
- 4. Entsprechend den Angaben auf der Seite „Determinante und inverse Matrix” gilt:
- $${\mathbf{I_y}} = {\mathbf{K_y}}^{-1} = \frac{1}{|{\mathbf{K_y}}|}\cdot \left[ \begin{array}{cc} 0.25 & -0.4 \\ -0.4 & 1 \end{array} \right].$$
- Mit |Ky| = 0.09 gilt deshalb weiter:
- $$I_{11} = \frac{25}{9}\hspace{0.15cm}\underline{ = 2.777};\hspace{0.3cm} I_{12} = I_{21} ='"`UNIQ--h-0--QINU`"'-\frac{40}{9} \hspace{0.15cm}\underline{ = -4.447};\hspace{0.3cm}I_{22} = \frac{100}{9} \hspace{0.15cm}\underline{= 11.111}.$$
- 5. Ein Vergleich der Matrizen Ky und Kx unter der Nebenbedingung K22 = 0 zeigt, dass x und y identische Zufallsgrößen sind, wenn man y1 = x1 und y2 = x3 setzt. Somit gilt für die WDF-Parameter:
- $$\sigma_1 =1, \hspace{0.3cm} \sigma_2 =0.5, \hspace{0.3cm} \rho = 0.8.$$
- Der Vorfaktor entsprechend Kapitel 4.2 ist somit:
- $$C =\frac{\rm 1}{\rm 2\pi \sigma_1 \sigma_2 \sqrt{\rm 1-\rho^2}}= \frac{\rm 1}{\rm 2\pi \cdot 1 \cdot 0.5 \cdot 0.6}= \frac{1}{0.6 \cdot \pi} \hspace{0.15cm}\underline{\approx 0.531}.$$
- Mit der in der Teilaufgabe 3) berechneten Determinante ergibt sich das gleiche Ergebnis:
- $$C =\frac{\rm 1}{\rm 2\pi \sqrt{|{\mathbf{K_y}}|}}= \frac{\rm 1}{\rm 2\pi \sqrt{0.09}} = \frac{1}{0.6 \cdot \pi}.$$
- 6. Die unter Punkt 4) berechnete inverse Matrix kann auch wie folgt geschrieben werden:
- $${\mathbf{I_y}} = \frac{5}{9}\cdot \left[ \begin{array}{cc} 5 & -8 \\ -8 & 20 \end{array} \right].$$
- Somit lautet das Argument A der Exponentialfunktion:
- $$A = \frac{5}{18}\cdot{\mathbf{y}}^{\rm T}\cdot \left[ \begin{array}{cc} 5 & -8 \\ -8 & 20 \end{array} \right]\cdot{\mathbf{y}} =\frac{5}{18}\left( 5 \cdot y_1^2 + 20 \cdot y_2^2 -16 \cdot y_1 \cdot y_2\right).$$
- Durch Koeffizientenvergleich ergibt sich:
- $$\gamma_1 = \frac{25}{18} \approx 1.389; \hspace{0.3cm} \gamma_2 = \frac{100}{18} \approx 5.556; \hspace{0.3cm} \gamma_{12} = - \frac{80}{18} \approx -4.444.$$
- Entsprechend der herkömmlichen Vorgehensweise ergeben sich die gleichen Zahlenwerte:
- $$\gamma_1 =\frac{\rm 1}{\rm 2\cdot \sigma_1^2 \cdot ({\rm 1-\rho^2})}= \frac{\rm 1}{\rm 2 \cdot 1 \cdot 0.36} \hspace{0.15cm}\underline{ \approx 1.389},$$
- $$\gamma_2 =\frac{\rm 1}{\rm 2 \cdot\sigma_2^2 \cdot ({\rm 1-\rho^2})}= \frac{\rm 1}{\rm 2 \cdot 0.25 \cdot 0.36} = 4 \cdot \gamma_1 \hspace{0.15cm}\underline{\approx 5.556},$$
- $$\gamma_{12} =-\frac{\rho}{ \sigma_1 \cdot \sigma_2 \cdot ({\rm 1-\rho^2})}= -\frac{\rm 0.8}{\rm 1 \cdot 0.5 \cdot 0.36} \hspace{0.15cm}\underline{ \approx -4.444}.$$