Stochastische Signaltheorie/Zweidimensionale Zufallsgrößen: Unterschied zwischen den Versionen
| Zeile 16: | Zeile 16: | ||
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf | des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf | ||
| − | *dem Lehrsoftwarepaket LNTsim | + | *dem Lehrsoftwarepaket [http://www.lntwww.de/downloads/Sonstiges/Programme/LNTsim.zip LNTsim] ⇒ Link verweist auf die ZIP-Version des Programms, |
| − | *der Praktikumsanleitung - Teil A | + | *der [http://www.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_A.pdf Praktikumsanleitung - Teil A] ⇒ Link verweist auf die PDF-Version mit Kapitel 4: Seite 81-80, |
| − | *der Praktikumsanleitung - Teil B | + | *der [http://www.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_B.pdf Praktikumsanleitung - Teil B] ⇒ Link verweist auf die PDF-Version mit Kapitel 13: Seite 295-314. |
==Eigenschaften und Beispiele== | ==Eigenschaften und Beispiele== | ||
Version vom 17. März 2017, 11:34 Uhr
Nun werden Zufallsgrößen mit statistischen Bindungen behandelt und anhand typischer Beispiele verdeutlicht. Nach der allgemeinen Beschreibung zweidimensionaler Zufallsgrößen wenden wir uns der Autokorrelationsfunktion (AKF) und der Kreuzkorrelationsfunktion (KKF) zu. Ebenso werden die dazugehörigen Spektralfunktionen angegeben.
Weitere Informationen zum Thema „Zweidimensionale Zufallsgrößen” sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 5: Zweidimensionale Zufallsgrößen (Programm zwd)
- Kapitel 9: Stochastische Prozesse (Programm sto)
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms,
- der Praktikumsanleitung - Teil A ⇒ Link verweist auf die PDF-Version mit Kapitel 4: Seite 81-80,
- der Praktikumsanleitung - Teil B ⇒ Link verweist auf die PDF-Version mit Kapitel 13: Seite 295-314.
Inhaltsverzeichnis
- 1 Eigenschaften und Beispiele
- 2 Verbundwahrscheinlichkeitsdichtefunktion
- 3 Zweidimensionale Verteilungsfunktion
- 4 WDF und VTF bei statistisch unabhängigen Komponenten
- 5 WDF und VTF bei statistisch abhängigen Komponenten
- 6 Erwartungswerte zweidimensionaler Zufallsgrößen (1)
- 7 Erwartungswerte zweidimensionaler Zufallsgrößen (2)
- 8 Korrelationskoeffizient
- 9 Korrelationsgerade
Eigenschaften und Beispiele
Als Überleitung zu den Korrelationsfunktionen betrachten wir nun zwei Zufallsgrößen $x$ und $y$, zwischen denen statistische Abhängigkeiten bestehen. Jede der beiden Zufallsgrößen kann für sich alleine mit den in Kapitel 2 bzw. Kapitel 3 eingeführten Kenngrößen beschrieben werden, je nachdem, ob es sich um eine diskrete oder um eine kontinuierliche Zufallsgröße handelt.
Zur Beschreibung der Wechselbeziehungen zwischen zwei Größen $x$ und $y$ ist es zweckmäßig, die beiden Komponenten zu einer zweidimensionalen Zufallsgröße $(x, y)$ zusammenzufassen. Die Einzelkomponenten können Signale sein wie der Real- und Imaginärteil eines phasenmodulierten Signals. Aber es gibt auch in anderen Bereichen eine Vielzahl von 2D-Zufallsgrößen.
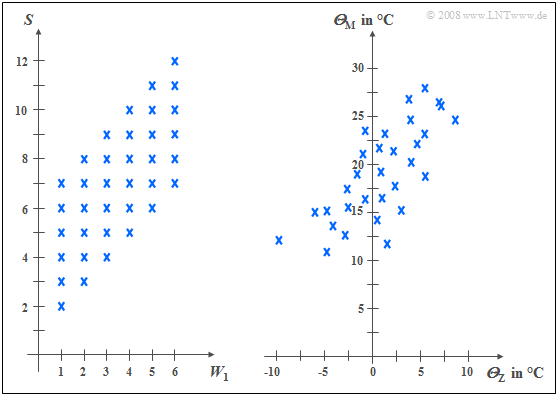
Das folgende linke Diagramm stammt von dem Zufallsexperiment Werfen mit zwei Würfeln. Nach rechts aufgetragen ist die Augenzahl des ersten Würfels $(W_1)$, nach oben die Summe $S$ beider Würfel. Die beiden Komponenten sind hier jeweils diskrete Zufallsgrößen, zwischen denen statistische Bindungen bestehen. Ist $W_1 =$ 1, so kann $S$ nur Werte zwischen 2 und 7 annehmen und zwar mit jeweils gleicher Warscheinlichkeit, bei $W_1 =$ 6 dagegen die Werte zwischen 7 und 12.
Rechts sind die Maximaltemperaturen der 31 Tage im Mai 2002 von München (nach oben) und der Zugspitze (nach rechts) gegenübergestellt. Beide Zufallsgrößen sind wertkontinuierlich. Obwohl die Messpunkte etwa 100 km auseinander liegen und es auf der Zugspitze aufgrund der unterschiedlichen Höhenlagen (knapp 3000 gegenüber 520 Meter) im Mittel um etwa 20 Grad kälter ist als in München, erkennt man doch eine gewisse statistische Abhängigkeit zwischen den beiden Größen $Θ_{\rm M}$ und $Θ_{\rm Z}$: Ist es in München warm, dann sind auch auf der Zugspitze eher angenehme Temperaturen zu erwarten. Der Zusammenhang ist aber nicht deterministisch: Der kälteste Tag im Mai 2002 war in München ein anderer als der kälteste Tag auf der Zugspitze.
Verbundwahrscheinlichkeitsdichtefunktion
Wir beschränken uns hier meist auf kontinuierliche Zufallsgrößen. Manchmal wird jedoch auch auf die Besonderheiten zweidimensionaler diskreter Zufallsgrößen genauer eingegangen.
Die meisten der bisherigen, für eindimensionale Zufallsgrößen definierten Kenngrößen können problemlos auf zweidimensionale Größen erweitert werden:
- Die Wahrscheinlichkeitsdichtefunktion der zweidimensionalen Zufallsgröße an der Stelle $(x_\mu, y_\mu)$, die man auch als Verbundwahrscheinlichkeitsdichtefunktion bezeichnet, ist eine Erweiterung der eindimensionalen WDF $(∩$ kennzeichnet die logische UND-Verknüpfung):
$$f_{\rm xy}(x_\mu, \hspace{0.1cm}y_\mu) = \hspace{12.0cm}\\ ...\hspace{0.1cm}= \lim_{\left.{\Delta x\rightarrow 0 \atop {\Delta y\rightarrow 0}}\right.} \frac{{\rm Pr}[(x_\mu-{\rm \Delta} x/{\rm 2 \le} x {\rm \le} x_\mu +{\rm \Delta} x/{\rm 2}) \cap (y_\mu-{\rm \Delta} y/{\rm 2} \le y \le y_\mu +{\rm \Delta}y/{\rm 2})]}{{\rm \Delta} \ x\cdot{\rm \Delta} y}.$$
- Bei diskreten Zufallsgrößen ist die Definition geringfügig zu modifizieren: Bei den jeweils unteren Bereichsgrenzen ist gemäß Kapitel 3.2 das „≤”–Zeichen durch das „<”–Zeichen zu ersetzen.
- Anhand dieser (Verbund)–WDF $f_{\rm xy}(x, y)$ werden auch statistische Abhängigkeiten innerhalb der zweidimensionalen Zufallsgröße $(x, y)$ vollständig erfasst im Gegensatz zu den beiden eindimensionalen Dichtefunktionen ⇒ Randwahrscheinlichkeitsdichtefunktionen:
$$f_{\rm x}(x) = \int _{-\infty}^{+\infty} f_{\rm xy}(x,y) \,\,{\rm d}y ,$$ $$f_{\rm y}(y) = \int_{-\infty}^{+\infty} f_{\rm xy}(x,y) \,\,{\rm d}x .$$
- Die beiden Randdichtefunktionen $f_x(x)$ und $f_y(y)$ liefern lediglich statistische Aussagen über die Einzelkomponenten $x$ bzw. $y$, nicht jedoch über die Bindungen zwischen diesen.
Zweidimensionale Verteilungsfunktion
Auch die 2D-Verteilungsfunktion ist lediglich eine sinnvolle Erweiterung der eindimensionalen Verteilungsfunktion (VTF): $$F_{\rm xy}(r_{\rm x},r_{\rm y}) = {\rm Pr}\left [(x \le r_{\rm x}) \cap (y \le r_{\rm y}) \right ] .$$ Der Funktionalzusammenhang zwischen zweidimensionaler WDF und zweidimensionaler VTF ist wie im eindimensionalen Fall durch die Integration gegeben, aber nun in zwei Dimensionen. Bei kontinuierlichen Zufallsgrößen gilt: $$F_{\rm xy}(r_{\rm x},r_{\rm y})=\int_{-\infty}^{r_{\rm y}} \int_{-\infty}^{r_{\rm x}} f_{\rm xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y .$$ Umgekehrt kann auch die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch partielle Differentiation nach $r_{\rm x}$ und $r_{\rm y}$ berechnet werden: $$f_{\rm xy}(x,y)=\frac{{\rm d}^{\rm 2} F_{\rm xy}(r_{\rm x},r_{\rm y})}{{\rm d} r_{\rm x} \,\, {\rm d} r_{\rm y}}\Bigg|_{\left.{r_{\rm x}=x \atop {r_{\rm y}=y}}\right.}.$$ Bezüglich der Verteilungsfunktion $F_{\rm xy}(r_{\rm x}, r_{\rm y})$ gelten folgende Grenzwerte: $$F_{\rm xy}(-\infty,-\infty) = 0,$$ $$F_{\rm xy}(r_{\rm x},\infty)=F_{\rm x}(r_{\rm x} ),$$ $$F_{\rm xy}(\infty,r_{\rm y})=F_{\rm y}(r_{\rm y} ) ,$$ $$F_{\rm xy}(\infty,\infty) = 1.$$ Im Grenzfall (unendlich große $r_{\rm x}$ und $r_{\rm y}$) ergibt sich demnach für die 2D-VTF der Wert 1. Daraus erhält man die Normierungsbedingung für die 2D-Wahrscheinlichkeitsdichtefunktion: $$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{\rm xy}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$
Beachten Sie den Unterschied zwischen eindimensionalen und zweidimensionalen Zufallsgrößen:
- Bei eindimensionalen Zufallsgrößen ergibt die Fläche unter der WDF stets den Wert 1.
- Bei zweidimensionalen Zufallsgrößen ist das WDF-Volumen immer gleich 1.
WDF und VTF bei statistisch unabhängigen Komponenten
Bei statistisch unabhängigen Komponenten $x$ und $y$ gilt für die Verbundwahrscheinlichkeit nach den elementaren Gesetzmäßigkeiten der Statistik, falls $x$ und $y$ wertkontinuierlich sind: $${\rm Pr} [(x_{\rm 1}\le x \le x_{\rm 2}) \cap( y_{\rm 1}\le y\le y_{\rm 2})] ={\rm Pr} (x_{\rm 1}\le x \le x_{\rm 2}) \cdot {\rm Pr}(y_{\rm 1}\le y\le y_{\rm 2}) .$$ Hierfür kann bei unabhängigen Komponenten auch geschrieben werden: $${\rm Pr} [(x_{\rm 1}\le x \le x_{\rm 2}) \cap(y_{\rm 1}\le y\le y_{\rm 2})] =\int _{x_{\rm 1}}^{x_{\rm 2}}f_{\rm x}(x) \,{\rm d}x\cdot \int_{y_{\rm 1}}^{y_{\rm 2}} f_{\rm y}(y) \, {\rm d}y.$$ Daraus folgt, dass bei statistischer Unabhängigkeit folgende Bedingung erfüllt sein muss: $$f_{\rm xy}(x,y)=f_{\rm x}(x) \cdot f_y(y) .$$
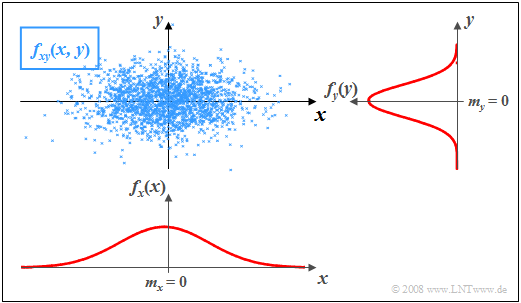
In der Grafik sind die Momentanwerte einer zweidimensionalen Zufallsgröße als Punkte in der $(x, y)$-Ebene eingetragen. Bereiche mit vielen Punkten, die dementsprechend dunkel wirken, kennzeichnen große Werte der WDF $f_{\rm xy}(x, y)$. Dagegen besitzt die Zufallsgröße $(x, y)$ in eher hellen Bereichen nur verhältnismäßig wenig Anteile.
Die Randwahrscheinlichkeitsdichten $f_{\rm x}(x)$ und $f_{\rm y}(y)$ lassen bereits erkennen, dass sowohl $x$ als auch $y$ gaußähnlich und mittelwertfrei sind, und dass die Zufallsgröße $x$ eine größere Streuung als $y$ aufweist. Sie liefern jedoch keine Informationen darüber, ob bei der Zufallsgröße $(x, y)$ statistische Bindungen zwischen den beiden Komponenten bestehen oder nicht.
Anhand der 2D-WDF ist zu erkennen, dass es hier keine statistischen Bindungen zwischen den Komponenten gibt. Bei statistischer Unabhängigkeit liefert jeder Schnitt durch $f_{\rm xy}(x, y)$ parallel zur $y$-Achse eine Funktion, die formgleich mit der Randwahrscheinlichkeitsdichtefunktion $f_{\rm y}(y)$ ist. Ebenso sind alle Schnitte parallel zur $x$-Achse formgleich mit $f_{\rm x}(x)$.
Diese Tatsache ist gleichbedeutend mit der Aussage, dass die 2D-WDF $f_{\rm xy}(x, y)$ als Produkt der beiden Randwahrscheinlichkeitsdichten dargestellt werden kann.
WDF und VTF bei statistisch abhängigen Komponenten
Bestehen statistische Bindungen zwischen den Komponenten, so liefern unterschiedliche Schnitte parallel zur $x$- bzw. $y$-Achse jeweils unterschiedliche, nicht formgleiche Funktionen. In diesem Fall lässt sich die Verbund-Wahrscheinlichkeitsdichtefunktion natürlich auch nicht als Produkt der beiden (eindimensionalen) Randwahrscheinlichkeitsdichten beschreiben.
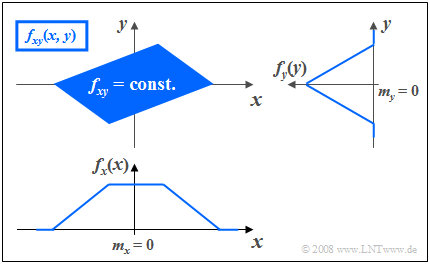
Die Grafik zeigt die Momentanwerte einer zweidimensionalen Zufallsgröße in der $(x, y)$-Ebene, wobei zwischen $x$ und $y$ nun statistische Bindungen bestehen. Die 2D-Zufallsgröße nimmt in dem blau eingezeichneten Parallelogramm alle Werte mit gleicher Wahrscheinlichkeit an, außerhalb sind keine Werte möglich.
Die Integration über die 2D-WDF $f_{\rm xy}(x, y)$ parallel zu der $x$-Achse führt zur dreieckförmigen Randdichte $f_{\rm y}(y)$, die Integration parallel zur $y$-Achse zur trapezförmigen WDF $f_{\rm x}(x)$.
Aus der zweidimensionalen Wahrscheinlichkeitsdichtefunktion $f_{\rm xy}(x, y)$ ist bereits zu erahnen, dass für jeden $x$-Wert im statistischen Mittel ein anderer $y$-Wert zu erwarten ist. Daran erkennt man ebenfalls, dass hier die Komponenten $x$ und $y$ statistisch voneinander abhängen.
Erwartungswerte zweidimensionaler Zufallsgrößen (1)
Ein Sonderfall der statistischen Abhängigkeit ist die Korrelation. Darunter versteht man eine lineare Abhängigkeit zwischen den Einzelkomponenten $x$ und $y$.
- Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig.
- Aber nicht jede statistische Abhängigkeit beschreibt gleichzeitig eine Korrelation.
Zur quantitativen Erfassung der Korrelation verwendet man verschiedene Erwartungswerte der 2D-Zufallsgröße $(x, y)$, die analog zum eindimensionalen Fall nach Kapitel 2.2 bzw. Kapitel 3.3 definiert sind:
- Für die (nichtzentrierten) Momente gilt die Beziehung:
$$m_{kl}={\rm E}[x^k\cdot y^l]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x^{k} \cdot y^{l} \cdot f_{\rm xy}(x,y) \, {\rm d}x\, {\rm d}y.$$
- Somit sind die beiden linearen Mittelwerte $m_x = m_{10}$ und $m_y = m_{01}.$
- Die auf $m_x$ bzw. $m_y$ bezogenen Zentralmomente lauten:
$$\mu_{kl} = {\rm E}[(x-m_{x})^k \cdot (y-m_{y})^l] .$$
- In dieser allgemein gültigen Definitionsgleichung sind die Varianzen $σ_x²$ und $σ_y²$ der zwei Einzelkomponenten durch $\mu_{20}$ bzw. $\mu_{02}$ mit enthalten.
- Besondere Bedeutung besitzt die sogenannte Kovarianz $(k = l =$ 1), die ein Maß für die lineare statistische Abhängigkeit zwischen den Zufallsgrößen $x$ und $y$ ist:
$$\mu_{11} = {\rm E}[(x-m_{x})\cdot(y-m_{y})] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) (y-m_{y})\cdot f_{\rm xy}(x,y) \,{\rm d}x \, {\rm d}y .$$
Im Folgenden bezeichnen wir die Kovarianz $\mu_{11}$ teilweise auch mit $\mu_{xy}$, falls sich die Kovarianz auf die Zufallsgrößen $x$ und $y$ bezieht. Die Kovarianz hängt wie folgt mit dem nichtzentrierten Moment $m_{11} = m_{xy} = E[x · y]$ zusammen:
$$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$
Diese Gleichung ist für die numerische Auswertung von enormen Vorteil, da $m_{xy}, m_x$ und $m_y$ aus den Folgen $〈x_v〉$ und $〈y_v〉$ direkt - also in einem Durchlauf - gefunden werden können. Würde man dagegen die Kovarianz $\mu_{xy}$ entsprechend der oberen Definitionsgleichung direkt berechnen, so müsste man in einem ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln und dann in einem zweiten Durchlauf den Erwartungswert ${\rm E}[(x – m_x) · (y – m_y)]$.
Erwartungswerte zweidimensionaler Zufallsgrößen (2)
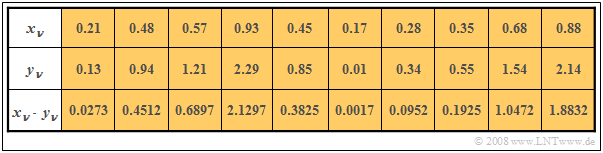
Nachfolgend sehen Sie die jeweils ersten Elemente zweier Zufallsfolgen $〈x_ν〉$ und $〈y_ν〉$. In der letzten Zeile sind die jeweiligen Produkte $x_ν · y_ν$ angegeben.
- Durch Mittelung über die jeweils zehn Folgenelemente erhält man $m_x =$ 0.5, $m_y =$ 1 und $m_{xy} =$ 0.69. Daraus ergibt sich die Kovarianz zu $\mu_{xy} =$ 0.69 – 0.5 · 1 = 0.19.
- Ohne Kenntnis der Gleichung $\mu_{xy} = m_{xy} – m_x · m_y$ hätte man zunächst im ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln müssen, um im zweiten Durchlauf die Kovarianz $\mu_{xy}$ als Erwartungswert des Produkts der mittelwertfreien Größen bestimmen zu können.
Korrelationskoeffizient
Bei statististischer Unabhängigkeit der beiden Komponenten $x$ und $y$ ist die Kovarianz $\mu_{xy} =$ 0. Das Ergebnis $„\mu_{xy} = 0”$ erhält man auch bei statististisch abhängigen Komponenten $x$ und $y$, wenn diese unkorreliert ⇒ linear unabhängig sind.
Sind dagegen $x$ und $y$ voll korreliert (z. B.: $y = K · x$), so ergibt sich bei positivem Wert von $K$ für die Kovarianz: $\mu_{xy} = σ_x · σ_y$. Deshalb verwendet man als Beschreibungsgröße häufig anstelle der Kovarianz den Korrelationskoeffizienten: $$\rho_{xy}=\frac{\mu_{xy}}{\sigma_x \cdot \sigma_y}.$$
Dieser weist folgende Eigenschaften auf:
- Aufgrund der Normierung gilt stets –1 ≤ $ρ_{xy}$ ≤ +1.
- Sind die beiden Zufallsgrößen $x$ und $y$ unkorreliert, so ist $ρ_{xy} =$ 0.
- Bei strenger linearer Abhängigkeit $(x$ und $y$ sind zueinander proportional) ist $ρ_{xy}=$ ±1.
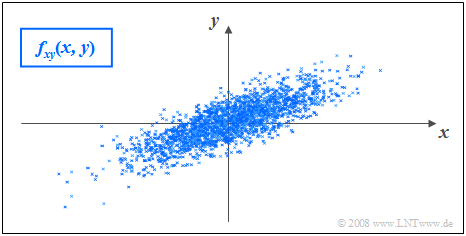
Die Zufallsgrößen $x$ und $y$ sind wie im Beispiel in Abschnitt 4 dieses Kapitels gaußförmig verteilt, wobei die Streuungen unterschiedlich sind ⇒ $σ_y$ < $σ_x$.
Im Unterschied zum ersten Beispiel sind aber nun die Zufallsgrößen $x$ und $y$ (positiv) korreliert. Der Korrelationskoeffizient ist dabei $ρ_{xy} =$ 0.8.
Fassen wir zusammen:
- Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$.
- Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $y$ mit steigendem $x$ im Mittel kleiner wird.
Korrelationsgerade
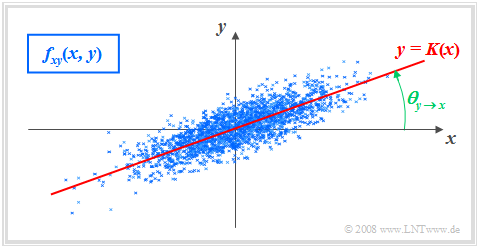
Man kann nun in die $(x, y)$-Ebene eine Gerade durch den „Mittelpunkt” $(m_x, m_y)$ einzeichnen. Diese Gerade $y = K(x)$ bezeichnet man als Korrelationsgerade (oder als Regressionsgerade).
Die Korrelationsgerade besitzt folgende Eigenschaften:
- Die mittlere quadratische Abweichung von dieser Geraden – in $y$-Richtung betrachtet und über alle $N$ Punkte gemittelt – ist minimal:
$$\overline{\varepsilon_y^{\rm 2}}=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}[y_\nu-K(x_{\nu})]^{\rm 2}={\rm Minimum}.$$
- Die Korrelationsgerade kann man als eine Art „statistische Symmetrieachse“ interpretieren. Die Geradengleichung lautet:
$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x-m_x)+m_y.$$
- Der Winkel, den die Korrelationsgerade zur $x$-Achse einnimmt, beträgt:
$$\theta_{y\rightarrow x}={\rm arctan}(\frac{\sigma_{y}}{\sigma_{x}}\cdot \rho_{xy}).$$
Durch diese Nomenklatur soll deutlich gemacht werden, dass es sich hier um die Regression von $y$ auf $x$ handelt. Die Regression in Gegenrichtung – also von $x$ auf $y$ – bedeutet dagegen die Minimierung der mittleren quadratischen Abweichung in $x$–Richtung.
Wie die folgende Animation verdeutlicht, ergibt sich dafür im Allgemeinen eine andere Gerade. Korrelationskoeffizient und Regressionsgerade