Aufgaben:Aufgabe 4.4: Gaußsche 2D-WDF: Unterschied zwischen den Versionen
| Zeile 27: | Zeile 27: | ||
{Welche der Aussagen gelten hinsichtlich der 2D-Zufallsgröße $(u, v)$? | {Welche der Aussagen gelten hinsichtlich der 2D-Zufallsgröße $(u, v)$? | ||
|type="[]"} | |type="[]"} | ||
| − | + Die Zufallsgrößen | + | + Die Zufallsgrößen $u$ und $v$ sind unkorreliert. |
| − | + Die Zufallsgrößen | + | + Die Zufallsgrößen $u$ und $v$ sind statistisch unabhängig. |
| Zeile 60: | Zeile 60: | ||
{Berechnen Sie nun die Wahrscheinlichkeit, dass die Zufallsgröße $x$ kleiner als $1$ und gleichzeitig die Zufallsgröße $y$ größer als $1$ ist. | {Berechnen Sie nun die Wahrscheinlichkeit, dass die Zufallsgröße $x$ kleiner als $1$ und gleichzeitig die Zufallsgröße $y$ größer als $1$ ist. | ||
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}[(x < 1) ∩ (y > 1)]\ = { 0.1359 3% } | + | ${\rm Pr}[(x < 1) ∩ (y > 1)]\ =$ { 0.1359 3% } |
| Zeile 68: | Zeile 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' <u>Beide Aussagen treffen zu</u>: | |
| − | :$$f_{uv}(u,v) = \frac{\rm 1}{{\rm 2}\it\pi \sigma_u\sigma_v\sqrt{{\rm 1}-\it \rho_{\it uv}^{\rm 2}}} \cdot \rm exp[\frac{\rm 1}{2\cdot (\rm 1-\it \rho_{uv}^{\rm 2})}(\frac{\it u^{\rm 2}}{\it\sigma_u^{\rm 2}} + \frac{\it v^{\rm 2}}{\it\sigma_v^{\rm 2}} - \rm 2\it\rho_{uv}\frac{\it u\cdot \it v}{\sigma_u\cdot \sigma_v})],$$ | + | *Vergleicht man die gegebene mit der allgemeingültigen 2D-WDF |
| + | :$$f_{uv}(u,v) = \frac{\rm 1}{{\rm 2}\it\pi \cdot \sigma_u \cdot \sigma_v\sqrt{{\rm 1}-\it \rho_{\it uv}^{\rm 2}}} \cdot \rm exp[\frac{\rm 1}{2\cdot (\rm 1-\it \rho_{uv}^{\rm 2})}(\frac{\it u^{\rm 2}}{\it\sigma_u^{\rm 2}} + \frac{\it v^{\rm 2}}{\it\sigma_v^{\rm 2}} - \rm 2\it\rho_{uv}\frac{\it u\cdot \it v}{\sigma_u\cdot \sigma_v}\rm )],$$ | ||
| − | :so erkennt man, dass im Exponenten kein Term mit | + | :so erkennt man, dass im Exponenten kein Term mit $u \cdot v$ auftritt, was nur bei $\rho_{uv} = 0$ möglich ist. |
| + | *Dies bedeutet aber, dass $u$ und $v$ unkorreliert sind. | ||
| + | *Bei Gaußschen Zufallsgrößen folgt aus der Unkorreliertheit aber auch stets die statistische Unabhängigkeit. | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(2)''' Bei statistischer Unabhängigkeit gilt: | |
| − | + | :$$f_{uv}(u, v) = f_u(u)\cdot f_v(v), \hspace{0.5cm} | |
| + | f_u(u)=\frac{{\rm e}^{-{\it u^{\rm 2}}/{(2\sigma_u^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_u} , \hspace{0.5cm} \it f_v(v)=\frac{{\rm e}^{-{\it v^{\rm 2}}/{({\rm 2}\sigma_v^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_v}.$$ | ||
| − | + | Durch Koeffizientenvergleich erhält man $\sigma_u = 0.5$ und $\sigma_v = 1$. Der Quotient ist somit $\sigma_u/\sigma_v\hspace{0.15cm}\underline{=0.5}$. | |
| + | |||
| + | |||
| + | '''(3)''' Da $u$ eine kontinuierliche Zufallsgröße ist, gilt: | ||
:$$\rm Pr(\it u < \rm 1) = \rm Pr(\it u \le \rm 1) =\it F_u(\rm 1). $$ | :$$\rm Pr(\it u < \rm 1) = \rm Pr(\it u \le \rm 1) =\it F_u(\rm 1). $$ | ||
| − | + | Mit dem Mittelwert $m_u = 0$ und der Streuung $\sigma_u = 0.5$ erhält man: | |
| − | :$$\rm Pr(\it u < \rm 1) = \rm \phi( | + | :$$\rm Pr(\it u < \rm 1) = \rm \phi({\rm 1}/{\it\sigma_u})= \rm \phi(\rm 2) \hspace{0.15cm}\underline{=\rm 0.9772}. $$ |
| − | : | + | [[Datei:P_ID265__Sto_A_4_4_d.png|right|2D-Gebietswahrscheinlichkeit ]] |
| − | :$$\rm Pr | + | '''(4)''' Aufgrund der statistischen Unabhängigkeit zwischen $u$ und $v$ gilt: |
| + | :$$\rm Pr[(\it u < \rm 1) \cap (\it v > \rm 1)] = \rm Pr(\it u < \rm 1)\cdot \rm Pr(\it v > \rm 1).$$ | ||
| − | + | Die Wahrscheinlichkeit ${\rm Pr}(u < 1) =0.9772$ wurde bereits berechnet. Für die zweite Wahrscheinlichkeit ${\rm Pr}(v > 1)$ gilt aus Symmetriegründen: | |
:$$\rm Pr(\it v > \rm 1) = \rm Pr(\it v \le \rm -1) = \it F_v(\rm -1) = \rm \phi(\frac{\rm -1}{\it\sigma_v}) = \rm Q(1) =0.1587$$ | :$$\rm Pr(\it v > \rm 1) = \rm Pr(\it v \le \rm -1) = \it F_v(\rm -1) = \rm \phi(\frac{\rm -1}{\it\sigma_v}) = \rm Q(1) =0.1587$$ | ||
:$$\Rightarrow \rm Pr((\it u < \rm 1) \cap (\it v > \rm 1)) = \rm 0.9772\cdot \rm 0.1587 \hspace{0.15cm}\underline{ = \rm 0.1551}.$$ | :$$\Rightarrow \rm Pr((\it u < \rm 1) \cap (\it v > \rm 1)) = \rm 0.9772\cdot \rm 0.1587 \hspace{0.15cm}\underline{ = \rm 0.1551}.$$ | ||
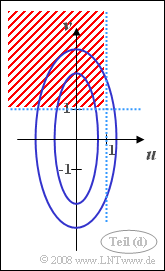
| − | + | Die Skizze verdeutlicht die vorgegebene Konstellation. Die Höhenlinien der WDF (blau) sind wegen $\sigma_v > \sigma_u$ in vertikaler Richtung gestreckte Ellipsen. Rot schraffiert eingezeichnet ist das Gebiet, dessen Wahrscheinlichkeit in dieser Teilaufgabe berechnet werden sollte. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | :Wie aus der Skizze hervorgeht, sind die WDF–Werte auf der Geraden | + | [[Datei:P_ID266__Sto_A_4_4_e.png|right|2D-Diracwand]] |
| + | '''(5)''' Richtig sind <u>der erste und der dritte Lösungsvorschlag</u>: | ||
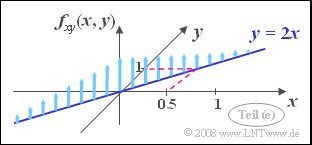
| + | *Wegen $\rho_{xy} = 1$ besteht ein deterministischer Zusammenhang zwischen $x$ und $y$ ⇒ alle Werte liegen auf der Geraden $y =K(x) \cdot; x$. Aufgrund der Streuungen $\sigma_x = 0.5$ und $\sigma_y = 1$ gilt $K = 2$. | ||
| + | *Auf dieser Geraden $y = 2x$ sind alle WDF-Werte unendlich groß. Das bedeutet: Die 2D-WDF ist hier eine „Diracwand”. | ||
| + | *Wie aus der Skizze hervorgeht, sind die WDF–Werte auf der Geraden$y = 2x$, die gleichzeitig die Korrelationsgerade darstellt, gaußverteilt. | ||
| + | *Auch die beiden Randwahrscheinlichkeitsdichten sind Gaußfunktionen, jeweils mit Mittelwert $0$. Wegen $\sigma_x = \sigma_u$ und $\sigma_y = \sigma_v$ gilt auch: | ||
:$$f_x(x) = f_u(u), \hspace{0.5cm}f_y(y) = f_v(v).$$ | :$$f_x(x) = f_u(u), \hspace{0.5cm}f_y(y) = f_v(v).$$ | ||
| − | : | + | [[Datei:P_ID274__Sto_A_4_4_g.png|right|Wahrscheinlichkeitsberechnung bei Diracwand]] |
| − | + | '''(6)''' Da die WDF der Zufallsgröße $x$ identisch mit der WDF $f_u(u)$ ist, ergibt sich auch genau die gleiche Wahrscheinlichkeit wie in der Teilaufgabe (3) berechnet: | |
| − | |||
| − | |||
:$$\rm Pr(\it x < \rm 1) \hspace{0.15cm}\underline{ = \rm 0.9772}.$$ | :$$\rm Pr(\it x < \rm 1) \hspace{0.15cm}\underline{ = \rm 0.9772}.$$ | ||
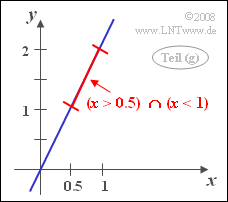
| − | + | '''(7)''' Das Zufallsereignis $y > 1$ ist identisch mit dem Ereignis $x > 0.5$. Damit ist die gesuchte Wahrscheinlichkeit gleich | |
| − | :$$ | + | :$$\rm Pr[(\it x > \rm 0.5) \cap (\it x < \rm 1)] = \it F_x \rm( 1) - \it F_x\rm (0.5). $$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Mit der Streuung $\sigma_x = 0.5$ folgt weiter: | ||
| + | :$$\rm Pr[(\it x > \rm 0.5) \cap (\it x < \rm 1)] = \rm \phi(\rm 2) - \phi(1)=\rm 0.9772- \rm 0.8413\hspace{0.15cm}\underline{=\rm 0.1359}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 20. März 2017, 11:28 Uhr
Wir betrachten zweidimensionale Zufallsgrößen, wobei beide Komponenten stets als mittelwertfrei vorausgesetzt werden. Die 2D-WDF der Zufallsgröße $(u, v)$ lautet:
- $$f_{uv}(u, v)=\frac{1}{\pi} \cdot {\rm e}^{-(2u^{\rm 2} \hspace{0.05cm}+ \hspace{0.05cm}v^{\rm 2}\hspace{-0.05cm}/\rm 2)}.$$
Von der ebenfalls Gaußschen 2D-Zufallsgröße $(x, y)$ sind die folgenden Parameter bekannt:
- $$\sigma_x= 0.5, \hspace{0.5cm}\sigma_y = 1,\hspace{0.5cm}\rho_{xy} = 1. $$
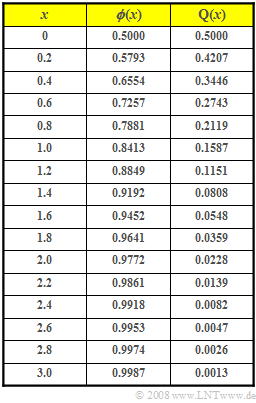
Die Werte des Gaußschen Fehlerintegrals ${\rm \phi}(x)$ sowie der Komplementärfunktion ${\rm Q}(x) = 1- {\rm \phi}(x)$ können Sie der nebenstehenden Tabelle entnehmen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.
- Bezuig genommen wird auch auf das Kapitel Gaußverteilte Zufallsgrößen
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Die hier behandelte Thematik ist in zwei Lernvideos zusammengefasst:
- Gaußsche Zufallsgrößen ohne statistische Bindungen
- Gaußsche Zufallsgrößen mit statistischen Bindungen
Fragebogen
Musterlösung
- Vergleicht man die gegebene mit der allgemeingültigen 2D-WDF
- $$f_{uv}(u,v) = \frac{\rm 1}{{\rm 2}\it\pi \cdot \sigma_u \cdot \sigma_v\sqrt{{\rm 1}-\it \rho_{\it uv}^{\rm 2}}} \cdot \rm exp[\frac{\rm 1}{2\cdot (\rm 1-\it \rho_{uv}^{\rm 2})}(\frac{\it u^{\rm 2}}{\it\sigma_u^{\rm 2}} + \frac{\it v^{\rm 2}}{\it\sigma_v^{\rm 2}} - \rm 2\it\rho_{uv}\frac{\it u\cdot \it v}{\sigma_u\cdot \sigma_v}\rm )],$$
- so erkennt man, dass im Exponenten kein Term mit $u \cdot v$ auftritt, was nur bei $\rho_{uv} = 0$ möglich ist.
- Dies bedeutet aber, dass $u$ und $v$ unkorreliert sind.
- Bei Gaußschen Zufallsgrößen folgt aus der Unkorreliertheit aber auch stets die statistische Unabhängigkeit.
(2) Bei statistischer Unabhängigkeit gilt:
- $$f_{uv}(u, v) = f_u(u)\cdot f_v(v), \hspace{0.5cm} f_u(u)=\frac{{\rm e}^{-{\it u^{\rm 2}}/{(2\sigma_u^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_u} , \hspace{0.5cm} \it f_v(v)=\frac{{\rm e}^{-{\it v^{\rm 2}}/{({\rm 2}\sigma_v^{\rm 2})}}}{\sqrt{\rm 2\pi}\cdot\sigma_v}.$$
Durch Koeffizientenvergleich erhält man $\sigma_u = 0.5$ und $\sigma_v = 1$. Der Quotient ist somit $\sigma_u/\sigma_v\hspace{0.15cm}\underline{=0.5}$.
(3) Da $u$ eine kontinuierliche Zufallsgröße ist, gilt:
- $$\rm Pr(\it u < \rm 1) = \rm Pr(\it u \le \rm 1) =\it F_u(\rm 1). $$
Mit dem Mittelwert $m_u = 0$ und der Streuung $\sigma_u = 0.5$ erhält man:
- $$\rm Pr(\it u < \rm 1) = \rm \phi({\rm 1}/{\it\sigma_u})= \rm \phi(\rm 2) \hspace{0.15cm}\underline{=\rm 0.9772}. $$
(4) Aufgrund der statistischen Unabhängigkeit zwischen $u$ und $v$ gilt:
- $$\rm Pr[(\it u < \rm 1) \cap (\it v > \rm 1)] = \rm Pr(\it u < \rm 1)\cdot \rm Pr(\it v > \rm 1).$$
Die Wahrscheinlichkeit ${\rm Pr}(u < 1) =0.9772$ wurde bereits berechnet. Für die zweite Wahrscheinlichkeit ${\rm Pr}(v > 1)$ gilt aus Symmetriegründen:
- $$\rm Pr(\it v > \rm 1) = \rm Pr(\it v \le \rm -1) = \it F_v(\rm -1) = \rm \phi(\frac{\rm -1}{\it\sigma_v}) = \rm Q(1) =0.1587$$
- $$\Rightarrow \rm Pr((\it u < \rm 1) \cap (\it v > \rm 1)) = \rm 0.9772\cdot \rm 0.1587 \hspace{0.15cm}\underline{ = \rm 0.1551}.$$
Die Skizze verdeutlicht die vorgegebene Konstellation. Die Höhenlinien der WDF (blau) sind wegen $\sigma_v > \sigma_u$ in vertikaler Richtung gestreckte Ellipsen. Rot schraffiert eingezeichnet ist das Gebiet, dessen Wahrscheinlichkeit in dieser Teilaufgabe berechnet werden sollte.
(5) Richtig sind der erste und der dritte Lösungsvorschlag:
- Wegen $\rho_{xy} = 1$ besteht ein deterministischer Zusammenhang zwischen $x$ und $y$ ⇒ alle Werte liegen auf der Geraden $y =K(x) \cdot; x$. Aufgrund der Streuungen $\sigma_x = 0.5$ und $\sigma_y = 1$ gilt $K = 2$.
- Auf dieser Geraden $y = 2x$ sind alle WDF-Werte unendlich groß. Das bedeutet: Die 2D-WDF ist hier eine „Diracwand”.
- Wie aus der Skizze hervorgeht, sind die WDF–Werte auf der Geraden$y = 2x$, die gleichzeitig die Korrelationsgerade darstellt, gaußverteilt.
- Auch die beiden Randwahrscheinlichkeitsdichten sind Gaußfunktionen, jeweils mit Mittelwert $0$. Wegen $\sigma_x = \sigma_u$ und $\sigma_y = \sigma_v$ gilt auch:
- $$f_x(x) = f_u(u), \hspace{0.5cm}f_y(y) = f_v(v).$$
(6) Da die WDF der Zufallsgröße $x$ identisch mit der WDF $f_u(u)$ ist, ergibt sich auch genau die gleiche Wahrscheinlichkeit wie in der Teilaufgabe (3) berechnet:
- $$\rm Pr(\it x < \rm 1) \hspace{0.15cm}\underline{ = \rm 0.9772}.$$
(7) Das Zufallsereignis $y > 1$ ist identisch mit dem Ereignis $x > 0.5$. Damit ist die gesuchte Wahrscheinlichkeit gleich
- $$\rm Pr[(\it x > \rm 0.5) \cap (\it x < \rm 1)] = \it F_x \rm( 1) - \it F_x\rm (0.5). $$
Mit der Streuung $\sigma_x = 0.5$ folgt weiter:
- $$\rm Pr[(\it x > \rm 0.5) \cap (\it x < \rm 1)] = \rm \phi(\rm 2) - \phi(1)=\rm 0.9772- \rm 0.8413\hspace{0.15cm}\underline{=\rm 0.1359}.$$