Aufgaben:Aufgabe 4.3Z: Exponential– und Laplaceverteilung: Unterschied zwischen den Versionen

Version vom 21. März 2017, 20:46 Uhr

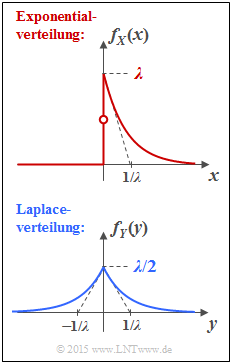
Wir betrachten hier die Wahrscheinlichkeitsdichtefunktionen (WDF) zweier wertkontinuierlicher Zufallsgrößen:

X ist exponentialverteilt (siehe obere Darstellung): Für x < 0 ist f_X(x) = 0, und für positive x–Werte gilt:

$$f_X(x) = \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.05cm}. $$

Dagegen gilt für die laplaceverteilte Zufallsgröße Y im gesamten Bereich –∞ < y < +∞ (untere Skizze):

$$f_Y(y) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|y|}\hspace{0.05cm}.$$ Zu berechnen sind die differentiellen Entropien h(X) und h(Y) abhängig vom WDF–Parameter λ. Zum Beispiel gilt: $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$ Bei Verwendung von „log₂” ist die Pseudo–Einheit „bit” anzufügen.

In den Teilaufgaben (b) und (d) ist die differentielle Entropie in folgender Form anzugeben: $$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L} \cdot \sigma^2) \hspace{0.5cm}{\rm bzw.} \hspace{0.5cm}h(Y) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L} \cdot \sigma^2) \hspace{0.05cm}.$$ Zu ermitteln ist, durch welche Faktoren Γ_L die Exponentialverteilung und die Laplaceverteilung charakterisiert werden.

Hinweis: Die Aufgabe bezieht sich auf das Themengebiet von Kapitel 4.1 Für die Varianzen der beiden betrachteten Zufallsgrößen gilt, wie in Aufgabe Z4.1 hergeleitet:

Exponentialverteilung ⇒ Zufallsgröße X: σ² = 1/λ²,
Laplaceverteilung ⇒ Zufallsgröße Y: σ² = 2/λ².

Fragebogen

Musterlösung

1. 2. 3. 4. 5. 6. 7.

@@ Zeile 33: / Zeile 33: @@
-{Input-Box Frage
+{Berechnen Sie die differentielle Entropie der Exponentialverteilung.
 |type="{}"}
-$\alpha$ = { 0.3 }
+$λ = 1:   h(X) $ = { 1.443 3% }
+{Welche Kenngröße ergibt sich für die Form <i>h</i>(<i>X</i>) = 1/2 &middot; log<sub>2</sub> (<i>&Gamma;</i><sub>L</sub> &middot; <i>&sigma;</i><sup>2</sup>)?
+|type="{}"}
+$Exponentialverteilung:   ΓL$ = { 7.39 3% }
+{Berechnen Sie die differentielle Entropie der Laplaceverteilung.
+|type="{}"}
+$ λ = 1:    h(Y) $ = { 2.443 3% }
+{Welche Kenngröße ergibt sich für die Form <i>h</i>(<i>Y</i>) = 1/2 &middot; log<sub>2</sub> (<i>&Gamma;</i><sub>L</sub> &middot; <i>&sigma;</i><sup>2</sup>)?
+|type="{}"}
+$Laplaceverteilung:   ΓL$ = { 14.78 3% }

	Falsch
	Richtig