Aufgaben:Aufgabe 4.4: Herkömmliche Entropie und differenzielle Entropie

• Zurück zum Buch

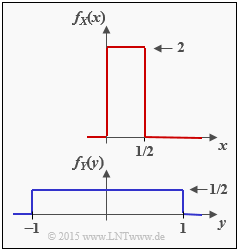
Wir betrachten die zwei wertkontinuierlichen Zufallsgrößen X und Y mit den Wahrscheinlichkeitsdichtefunktionen f_X(x) und f_Y(y). Für diese Zufallsgrößen kann man

• die herkömmlichen Entropien H(X), H(Y) nicht angeben,
• jedoch aber die differentiellen Entropien h(X) und h(Y).

Wir betrachten außerdem zwei wertdiskrete Zufallsgrößen:

• Z_X,M ergibt sich durch (geeignete) Quantisierung der Zufallsgröße X mit der Quantisierungsstufenzahl M  ⇒  Quantisierungsintervallbreite Δ = 0.5/M.
• Die Zufallsgröße Z_Y,M ergibt sich nach Quantisierung der wertkontinuierlichen Zufallsgröße Y mit der Quantisierungsstufenzahl M  ⇒  Quantisierungsintervallbreite Δ = 2/M.

Die Wahrscheinlichkeitsdichtefunktionen dieser diskreten Zufallsgrößen setzen sich jeweils aus M Diracfunktionen zusammen, deren Impulsgewichte durch die Intervallflächen der zugehörigen wertkontinuierlichen Zufallsgrößen gegeben sind. Daraus lassen sich die Entropien H(Z_X,M) und H(Z_Y,M) in herkömmlicher Weise (entsprechend Kapitel 3) bestimmen.

Im Theorieteil wurde auch eine Näherung angegeben. Beispielsweise gilt: $$H(Z_{X, \hspace{0.05cm}M}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X)\hspace{0.05cm}. $$ Sie werden im Laufe der Aufgabe feststellen, dass bei rechteckförmiger WDF ⇒ Gleichverteilung diese „Näherung” genau das gleiche Ergebnis liefert wie die direkte Berechnung. Aber im allgemeinen Fall – zum Beispiel bei dreieckförmiger WDF – stellt obige Gleichung tatsächlich nur eine Näherung dar, die erst im Grenzfall Δ → 0 mit der tatsächlichen Entropie H(Z_X,M) übereinstimmt.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.1

Fragebogen

1

Berechnen Sie die differentielle Entropie h(X).

$ h(X)$ =

2

Berechnen Sie die differentielle Entropie h(Y).

$ h(Y)$ =

3

Berechnen Sie die Entropie der wertdiskreten Zufallsgrößen Z_{X, M = 4}.

$direkte Berechnung: H(Z_{ X, M = 4})$ =

$mit Näherung: H(Z_{ X, M = 4})$ =

4

Berechnen Sie die Entropie der wertdiskreten Zufallsgröße Z_{Y, M = 4}.

$mit Näherung: H(Z_{ Y, M = 4})$ =

5

Berechnen Sie die Entropie der wertdiskreten Zufallsgröße Z_{Y, M = 8}.

$mit Näherung: H(Z_{ Y, M = 8})$ =

6

Welche der folgenden Aussagen sind zutreffend?

	Die Entropie einer diskreten Zufallsgröße Z ist stets H(Z) ≥ 0.
	Die differentielle Entropie einer kontinuierlichen Zufallsgröße X ist stets h(X) ≥ 0.

Musterlösung

Musterlösung

a)  Gemäß der entsprechenden Theorieseite gilt mit x_min = 0 und x_max = 1/2: $$h(X) = {\rm log}_2 \hspace{0.1cm} (x_{\rm max} - x_{\rm min}) = {\rm log}_2 \hspace{0.1cm} (1/2) \hspace{0.15cm}\underline{= - 1\,{\rm bit}}\hspace{0.05cm}.$$

b)  Mit y_min = –1 und y_max = +1 ergibt sich für die differentielle Entropie der Zufallsgröße Y: $$h(Y) = {\rm log}_2 \hspace{0.1cm} (x_{\rm max} - x_{\rm min}) = {\rm log}_2 \hspace{0.1cm} (2) \hspace{0.15cm}\underline{= + 1\,{\rm bit}}\hspace{0.05cm}. $$

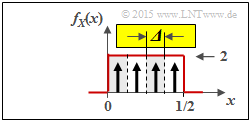
c)  Die nachfolgende Grafik verdeutlicht die bestmögliche Quantisierung der Zufallsgröße X mit der Quantisierungsstufenzahl M = 4  ⇒  Zufallsgröße Z_{X, M = 4}:

• Die Intervallbreite ist hier gleich Δ = 0.5/4 = 1/8.
• Die möglichen Werte (jeweils in der Intervallmitte) sind z ∈ {0.0625, 0.1875, 0.3125, 0.4375}.
• Die direkte Berechnung der Entropie ergibt mit der Wahrscheinlichkeitsfunktion P_Z(Z) = [1/4, ... , 1/4]:

$$H(Z_{X, M = 4}) = {\rm log}_2 \hspace{0.1cm} (4) \hspace{0.15cm}\underline{= 2\,{\rm bit}} \hspace{0.05cm}.$$

• Mit der Näherung erhält man unter Berücksichtigung des Ergebnisses der Teilaufgabe (a):

$$H(Z_{X, M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X) = 3\,{\rm bit} +(- 1\,{\rm bit})\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}. $$ Hinweis: Nur bei der Gleichverteilung liefert die Näherung genau das gleiche Ergebnis.

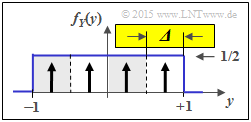
d)  Aus der zweiten Grafik erkennt man die Gemeinsamkeiten / Unterschiede zur Teilaufgabe (c):

• Der Quantisierungsparameter ist nun Δ = 2/4 = 1/2.
• Die möglichen Werte sind nun z ∈ {±0.75, ±0.25}.
• Somit liefert hier die „Näherung” (ebenso wie die direkte Berechnung) das Ergebnis:

$$H(Z_{Y, M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y)$$ $$ =\ \hspace{-0.15cm} 1\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}.$$

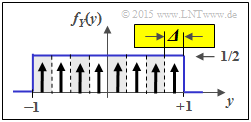
e)  Im Gegensatz zur Teilaufgabe (d) gilt nun Δ = 1/4. Daraus folgt für die „Näherung”: $$H(Z_{Y, M = 8}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y)$$ $$ =\ \hspace{-0.15cm} 2\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 3\,{\rm bit}}\hspace{0.05cm}.$$ Wieder gleiches Ergebnis bei direkter Berechnung.

f)  Richtig ist nur die Aussage 1:

• Die Entropie H(Z) einer diskreten Zufallsgröße Z = {z₁, ... , z_M} kann nie negativ werden. Der Grenzfall H(Z) = 0 ergibt sich z.B. für Pr(Z = z₁) = 1 und Pr(Z = z_μ) = 0 für 2 ≤ μ ≤ M.

• Dagegen kann die differentielle Entropie h(X) einer kontinuierlichen Zufallsgröße X negativ (Teilaufgabe a), positiv (Teilaufgabe b) oder auch h(X) = 0 (z.B. x_min = 0, x_max = 1) sein.