Aufgaben:Aufgabe 4.16: Eigenwerte und Eigenvektoren

• Zurück zum Buch

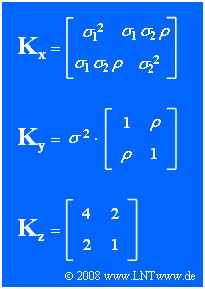
Obwohl die Beschreibung Gaußscher Zufallsgrößen mit Hilfe von Vektoren und Matrizen eigentlich nur bei mehr als $N = 2$ Dimensionen erforderlich ist und Sinn macht, beschränken wir uns hier auf den Sonderfall zweidimensionaler Zufallsgrößen.

In der Grafik ist oben die allgemeine Korrelationsmatrix $\mathbf{K_x}$ der 2D–Zufallsgröße $\mathbf{x} = (x_1, x_2)^{\rm T}$ angegeben, wobei $\sigma_1^2$ und $\sigma_2^2$ die Varianzen der Einzelkomponenten beschreiben. $\rho$ bezeichnet den Korrelationskoeffizienten zwischen den beiden Komponenten.

Die Zufallsgrößen $\mathbf{y}$ und $\mathbf{z}$ geben zwei Spezialfälle von $\mathbf{x}$ an, deren Prozessparameter aus den Kovarianzmatrizen $\mathbf{K_y}$ bzw. $\mathbf{K_z}$ bestimmt werden können.

Hinweise:

• Die Aufgabe gehört zum Kapitel Verallgemeinerung auf N-dimensionale Zufallsgrößen.
• Einige Grundlagen zur Anwendung von Vektoren und Matrizen finden sich auf den Seiten Determinante einer Matrix sowie Inverse einer Matrix
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Insbesondere ist zu beachten: Eine $2×2$-Kovarianzmatrix besitzt zwei reelle Eigenwerte $\lambda_1$ und $\lambda_2$. Diese beiden Eigenwerte bestimmen zwei Eigenvektoren $\xi_1$ und $\xi_2$. Diese spannen ein neues Koordinatensystem in Richtung der Hauptachsen des alten Systems auf.
• Entsprechend der Seite Höhenlinien bei korrelierten Zufallsgrößen ist der Winkel $\alpha$ zwischen dem alten und dem neuen System durch folgende Gleichung gegeben:

$$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2}).$$

Fragebogen

1

Welche Aussagen treffen für die Kovarianzmatrix $\mathbf{K_y}$ zu?

	$\mathbf{K_y}$ beschreibt alle möglichen 2D-Zufallsgrößen mit $\sigma_1 = \sigma_2 = \sigma$.
	Der Wertebereich des Parameters $\rho$ ist $-1 \le \rho \le +1$.
	Der Wertebereich des Parameters $\rho$ ist $0 < \rho < 1$.

2

Berechnen Sie die Eigenwerte von $\mathbf{K_y}$ unter der Bedingung $\sigma = 1$ und $\rho = 0$.

$\lambda_1 \ = $ $\ (\lambda_1 \ge \lambda_2)$

$\lambda_2 \ = $ $\ (\lambda_2 \le \lambda_1)$

3

Geben Sie die Eigenwerte von $\mathbf{K_y}$ unter der Bedingung $\sigma = 1$ sowie $0 < \rho < 1$ an.
Welche Werte ergeben sich für $\rho = 0.5 $, wobei $\lambda_1 \ge \lambda_2$ vorausgesetzt wird?

$\rho = 0.5\text{:} \;\lambda_1 \ = $ $\ (\lambda_1 \ge \lambda_2)$

$\rho = 0.5\text{:} \;\lambda_2 \ = $ $\ (\lambda_2 \le \lambda_1)$

4

Berechnen Sie die zugehörigen Eigenvektoren $\mathbf{\eta_1}$ und $\mathbf{\eta_2}$. Welche der folgenden Aussagen sind zutreffend?

	$\mathbf{\eta_1}$ und $\mathbf{\eta_2}$ liegen in Richtung der Ellipsenhauptachsen.
	Die neuen Koordinaten sind um $45^\circ$ gedreht.
	Die Streuungen bezüglich des neuen Systems sind $\lambda_1$ und $\lambda_2$.

5

Wie lauten die Kenngrößen der durch $\mathbf{K_z}$ festgelegten Zufallsgröße $\mathbf{z}$?

$\sigma_1$ =

$\sigma_2$ =

$\rho$ =

6

Berechnen Sie die Eigenwerte $\lambda_1$ und $\lambda_2 \le \lambda_1$ der Kovarianzmatrix $\mathbf{K_z}$.

$\lambda_1 \ = $ $\ (\lambda_1 \ge \lambda_2)$

$\lambda_2 \ = $ $\ (\lambda_2 \le \lambda_1)$

7

Um welchen Winkel $\alpha$ ist das neue Koordinatensystem $(\mathbf{\zeta_1}, \mathbf{\zeta_2})$ gegenüber dem ursprünglichen System $(\mathbf{z_1}, \mathbf{z_2})$ gedreht?

$\alpha \ = $ $\ \rm Grad$

Musterlösung

Musterlösung

(1)  Richtig sind die Lösungsvorschläge 1 und 2:

• $\mathbf{K_y}$ ist tatsächlich die allgemeinste Kovariationmatrix einer 2D-Zufallsgröße mit $\sigma_1 = \sigma_2 = \sigma$.
• Der Parameter $\rho$ gibt den Korrelationskoeffizienten an. Dieser kann alle Werte zwischen $\pm 1$ inclusive dieser Randwerte annehmen.

(2)  In diesem Fall lautet die Bestimmungsgleichung:

$${\rm det}\left[ \begin{array}{cc} 1- \lambda & 0 \\ 0 & 1- \lambda \end{array} \right] = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} (1- \lambda)^2 = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{\lambda_{1/2} =1}.$$

(3)  Bei positivem $\rho$ lautet die Bestimmungsgleichung der Eigenwerte:

$$(1- \lambda)^2 -\rho^2 = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\lambda^2 - 2\lambda + 1 - \rho^2 = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\lambda_{1/2} =1 \pm \rho.$$

Für $\rho= 0.5$ erhält man $\underline{\lambda_{1} =1.5}$ und $\underline{\lambda_{2} =0.5}$. Die Gleichung gilt übrigens im gesamten Definitionsbereich $-1 \le \rho \le +1$.

• Für $\rho = 0$ ist $\lambda_1 = \lambda_2 = +1$ (siehe Teilaufgabe 2).
• Bei $\rho = \pm 1$ ergibt sich $\lambda_1 = 2$ und $\lambda_2 = 0$.

(4)  Die Eigenvektoren erhält man durch Einsetzen der Eigenwerte $\lambda_1$ und $\lambda_2$ in die Kovarianzmatrix:

$$\left[ \begin{array}{cc} 1- (1+\rho) & \rho \\ \rho & 1- (1+\rho) \end{array} \right]\cdot{\boldsymbol{\eta_1}} = \left[ \begin{array}{cc} -\rho & \rho \\ \rho & -\rho \end{array} \right]\cdot \left[ \begin{array}{c} \eta_{11} \\ \eta_{12} \end{array} \right]=0$$

$$\Rightarrow\hspace{0.3cm}-\rho \cdot \eta_{11} + \rho \cdot \eta_{12} = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\eta_{11}= {\rm const} \cdot \eta_{12}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\boldsymbol{\eta_1}}= {\rm const}\cdot \left[ \begin{array}{c} 1 \\ 1 \end{array} \right];$$

$$\left[ \begin{array}{cc} 1- (1-\rho) & \rho \\ \rho & 1- (1-\rho) \end{array} \right]\cdot{\boldsymbol{\eta_2}} = \left[ \begin{array}{cc} \rho & \rho \\ \rho & \rho \end{array} \right]\cdot \left[ \begin{array}{c} \eta_{21} \\ \eta_{22} \end{array} \right]=0$$

$$\Rightarrow\hspace{0.3cm}\rho \cdot \eta_{21} + \rho \cdot \eta_{22} = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\eta_{21}= -{\rm const} \cdot \eta_{22}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\boldsymbol{\eta_2}}= {\rm const}\cdot \left[ \begin{array}{c} -1 \\ 1 \end{array} \right].$$

Bringt man diese in die so genannte Orthonormalform, so gilt:

$${\boldsymbol{\eta_1}}= \frac{1}{\sqrt{2}}\cdot \left[ \begin{array}{c} 1 \\ 1 \end{array} \right],\hspace{0.5cm} {\boldsymbol{\eta_2}}= \frac{1}{\sqrt{2}}\cdot \left[ \begin{array}{c} -1 \\ 1 \end{array} \right].$$

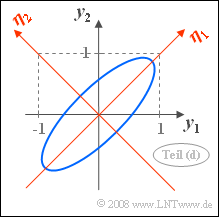
In der nebenstehenden Skizze ist das Ergebnis verdeutlicht:

• Das neue, durch $\mathbf{\eta_1}$ und $\mathbf{\eta_2}$ festgelegte Koordinatensystem liegt tatsächlich in Richtung der Hauptachsen des ursprünglichen Systems.
• Mit $\sigma_1 = \sigma_2$ ergibt sich fast immer (Ausnahme: $\rho= 0$) der Drehwinkel $\alpha = 45^\circ$. Dies folgt auch aus der im Theorieteil angegebenen Gleichung:

$$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2})= {1}/{2}\cdot \arctan (\infty)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\alpha = 45^\circ.$$

• Die Eigenwerte $\lambda_1$ und $\lambda_2$ kennzeichnen nicht die Streuungen bezüglich der neuen Achsen, sondern die entsprechenden Varianzen.

Richtig sind also die Lösungsvorschläge 1 und 2.

(5)  Durch Vergleich der Matrizen $\mathbf{K_x}$ und $\mathbf{K_z}$ erhält man

• $\sigma_{1}\hspace{0.15cm}\underline{ =2}$,
• $\sigma_{2}\hspace{0.15cm}\underline{ =1}$,
• $\rho = 2/(\sigma_{1} \cdot \sigma_{2})\hspace{0.15cm}\underline{ =1}$.

(6)  Nach dem inzwischen altbekannten Schema gilt:

$$(4- \lambda) \cdot (1- \lambda) -4 = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\lambda^2 - 5\lambda = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\hspace{0.15cm}\underline{\lambda_{1} =5,\hspace{0.1cm} \lambda_{2} =0}.$$

(7)  Nach der auf dem Angabenblatt vorgegebenen Gleichung gilt:

$$\alpha ={1}/{2}\cdot \arctan (2 \cdot 1 \cdot \frac{2 \cdot 1}{2^2 -1^2})= {1}/{2}\cdot \arctan ({4}/{3}) = 26.56^\circ.$$

Zum gleichen Ergebnis gelangt man über den Eigenvektor:

$$\left[ \begin{array}{cc} 4-5 & 2 \\ 2 & 1-5 \end{array} \right]\cdot \left[ \begin{array}{c} \zeta_{11} \\ \zeta_{12} \end{array} \right]=0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}-\zeta_{11}= 2\zeta_{12}=0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\zeta_{12}={\zeta_{11}}/{2}$$

$$\Rightarrow\hspace{0.3cm}\alpha = \arctan ({\zeta_{12}}/{\zeta_{11}}) = \arctan(0.5) \hspace{0.15cm}\underline{= 26.56^\circ}.$$

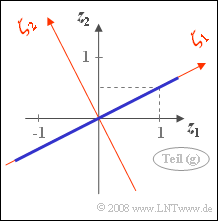
Die nebenstehende Skizze zeigt die 2D-WDF der Zufallsgröße $\mathbf{z}$:

• Wegen $\rho = 1$ liegen alle Werte auf der Korrelationsgeraden mit den Koordinaten $z_1$ und $z_2 = z_1/2$.
• Durch die Drehung um den Winkel $\alpha = \arctan(0.5) = 26.56^\circ$ entsteht ein neues Koordinatensystem.
• Die Varianz entlang der Achse $(\mathbf{\zeta_1}$ beträgt $\lambda_1 = 5$ (Streuung $\sigma_1 = \sqrt{5} = 2.236$), während in der dazu orthogonalen Richtung $(\mathbf{\zeta_2}$ die Zufallsgröße nicht ausgedehnt ist $(\lambda_2 = \sigma_2 = 0)$.