Aufgaben:Aufgabe 4.8Z: Was sagt die AWGN-Kanalkapazitätskurve aus?: Unterschied zwischen den Versionen

@@ Zeile 27: / Zeile 27: @@
 <quiz display=simple>
-{Multiple-Choice Frage
+{Welche Aussage liefert der <b>Punkt <i>X</i></b> für die Digitalsignalübertragung?
 |type="[]"}
-- Falsch
++ Für 10 &middot; lg (<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) = 4 dB ist ein Digitalsystem mit der Rate <nobr><i>R</i> = 1</nobr> und der Fehlerwahrscheinlichkeit 0 vorstellbar.
-+ Richtig
+- Ein solches System kommt ohne Kanalcodierung aus.
++ Ein solches System verwendet einen unendlich langen Code.
+- Auch ein Binärsystem kann die Voraussetzungen erfüllen.
+{Welche Aussage liefert der <b>Punkt <i>Y</i></b> für die Digitalsignalübertragung?
+|type="[]"}
+- Für 10 &middot; lg (<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) = 0 dB ist ein Digitalsystem mit der Rate <nobr><i>R</i> = 2</nobr> und der Fehlerwahrscheinlichkeit 0 vorstellbar.
++ Für 10 &middot; lg (<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) = 0 dB wäre <i>R</i> = 0.5 ausreichend.
+- Für die Rate <i>R</i> = 2 würde 10 &middot; lg (<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) = 5 dB genügen.
+{Welche Aussage liefert der <b>Punkt <i>Z</i></b> für die Binärübertragung?
+|type="[]"}
++ Ein Binärsystem erfüllt die Anforderungen auf keinen Fall.
+- Die Kurve <i>C</i><sub>Gauß</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) reicht für diese Bewertung nicht aus.
+{Welche Aussage liefert der <b>Punkt <i>Z</i></b> für die Quaternärübertragung?
+|type="[]"}
+- Ein Quaternärsystem erfüllt die Anforderungen auf keinen Fall.
++ Die Kurve <i>C</i><sub>Gauß</sub>(<i>E</i><sub>B</sub>/<i>N</i><sub>0</sub>) reicht für diese Bewertung nicht aus.
-{Input-Box Frage
-|type="{}"}
-$\alpha$ = { 0.3 }

Version vom 19. April 2017, 16:20 Uhr

Zurück zum Buch

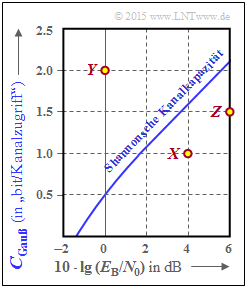
Wir betrachten wie in Aufgabe A4.8 die Kanalkapazität des AWGN–Kanals:

$$C_{\rm Gauß}( E_{\rm B}/{N_0}) = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) . $$

Die Kurve ist rechts bei logarithmischer Achse zwischen –2 dB und +6 dB dargestellt.
Der Zusatz „Gauß” weist darauf hin, dass für diese Kurve am AWGN–Eingang eine Gaußverteilung vorausgesetzt wurde.

Eingezeichnet sind in obiger Grafik drei Systemvarianten:

System X : 10 · lg (E_B/N₀) = 4 dB, R = 1,
System Y : 10 · lg (E_B/N₀) = 0 dB, R = 2,
System Z : 10 · lg (E_B/N₀) = 6 dB, R = 1.5.

Hinweis

Die Aufgabe bezieht sich auf das Kapitel 4.3.

In den Fragen zu dieser Aufgabe verwenden wir noch folgende Begriffe:

Digitalsystem: Symbolumfang M_X = |X| beliebig,
Binärsystem: Symbolumfang M_X = 2,
Quaternärsystem: Symbolumfang M_X = 4.

Fragebogen

Welche Aussage liefert der Punkt X für die Digitalsignalübertragung?

	Für 10 · lg (E_B/N₀) = 4 dB ist ein Digitalsystem mit der Rate <nobr>R = 1</nobr> und der Fehlerwahrscheinlichkeit 0 vorstellbar.
	Ein solches System kommt ohne Kanalcodierung aus.
	Ein solches System verwendet einen unendlich langen Code.
	Auch ein Binärsystem kann die Voraussetzungen erfüllen.

Welche Aussage liefert der Punkt Y für die Digitalsignalübertragung?

	Für 10 · lg (E_B/N₀) = 0 dB ist ein Digitalsystem mit der Rate <nobr>R = 2</nobr> und der Fehlerwahrscheinlichkeit 0 vorstellbar.
	Für 10 · lg (E_B/N₀) = 0 dB wäre R = 0.5 ausreichend.
	Für die Rate R = 2 würde 10 · lg (E_B/N₀) = 5 dB genügen.

Welche Aussage liefert der Punkt Z für die Binärübertragung?

	Ein Binärsystem erfüllt die Anforderungen auf keinen Fall.
	Die Kurve C_Gauß(E_B/N₀) reicht für diese Bewertung nicht aus.

Welche Aussage liefert der Punkt Z für die Quaternärübertragung?

	Ein Quaternärsystem erfüllt die Anforderungen auf keinen Fall.
	Die Kurve C_Gauß(E_B/N₀) reicht für diese Bewertung nicht aus.

Musterlösung

1. 2. 3. 4. 5. 6. 7.