Aufgaben:Aufgabe 4.9: Höherstufige Modulation: Unterschied zwischen den Versionen

Aus LNTwww
Wechseln zu:Navigation, Suche
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/AWGN–Kanalkapazität bei wertdiskretem Eingang }} right| Die Grafik zeigt AW…“)
 
Zeile 25: Zeile 25:
  
 
<quiz display=simple>
 
<quiz display=simple>
−
{Multiple-Choice Frage
+
{Welche Gleichung liegt der Shannon&ndash;Grenzkurve <i>C</i><sub>Gauß</sub> zugrunde?
 
|type="[]"}
 
|type="[]"}
−
- Falsch
+
- Es gilt <i>C</i><sub>Gauß</sub> = <i>C</i><sub>1</sub> = 1/2 &middot; log<sub>2</sub> (1 + <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>),
−
+ Richtig
+
+ Es gilt <i>C</i><sub>Gauß</sub> = <i>C</i><sub>2</sub> = 1/2 &middot; log<sub>2</sub> (1 + 2<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>),
 +
- Es gilt <i>C</i><sub>Gauß</sub> = <i>C</i><sub>3</sub> = log<sub>2</sub> (1 + <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>).
  
  
−
{Input-Box Frage
+
{Welche Aussagen treffen für die grüne Kurve <i>C</i><sub>BPSK</sub> zu?
−
|type="{}"}
+
|type="[]"}
−
$\alpha$ = { 0.3 }
+
+ <i>C</i><sub>BPSK</sub> kann nicht in geschlossener Form angegeben werden.
 +
+ <i>C</i><sub>BPSK</sub> ist größer als 0, wenn <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub> > 0 vorausgesetzt wird.
 +
- Für <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub> < ln (2) ist <i>C</i><sub>BPSK</sub> &equiv; 0.
 +
+ Im gesamten Bereich gilt <i>C</i><sub>BPSK</sub> < <i>C</i><sub>Gauß</sub>.
 +
 
 +
{Welche Aussagen treffen für die rote Kurve zu?
 +
|type="[]"}
 +
- Für die zugehörige Zufallsgröße <i>X</i> gilt <i>M<sub>X</sub></i> = |<i>X</i>| = 2.
 +
+ Für die zugehörige Zufallsgröße <i>X</i> gilt <i>M<sub>X</sub></i> = |<i>X</i>| = 4.
 +
+ <i>C</i><sub>rot</sub> ist gleichzeitig die Kanalkapazität der 4&ndash;ASK.
 +
- <i>C</i><sub>rot</sub> ist gleichzeitig die Kanalkapazität der 4&ndash;QAM.
 +
+ Für alle <i>E</i><sub>S</sub>/<i>N</i><sub>0</sub> > 0 liegt <i>C</i><sub>rot</sub> zwischen &bdquo;grün&rdquo; und &bdquo;braun&rdquo;.
 +
 
 +
 
 +
{Welche Aussagen treffen für die braune Kurve zu?
 +
|type="[]"}
 +
+ Für die zugehörige Zufallsgröße gilt <i>M<sub>X</sub></i> = |<i>X</i>| = 8.
 +
+ <i>C</i><sub>braun</sub></i> ist gleichzeitig die Kanalkapazität der 8&ndash;ASK.
 +
- <i>C</i><sub>braun</sub></i> ist gleichzeitig die Kanalkapazität der 8&ndash;PSK..
 +
- <i>p</i><sub>B</sub> = 0 ist mit 8&ndash;ASK, <i>R</i> = 2.5 und (<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>)<sub>dB</sub> = 10 dB möglich.
 +
+ <i>p</i><sub>B</sub> = 0 ist mit 8&ndash;ASK, <i>R</i> = 2 und (<i>E</i><sub>S</sub>/<i>N</i><sub>0</sub>)<sub>dB</sub> = 10 dB möglich.
  
  

Version vom 19. April 2017, 16:56 Uhr

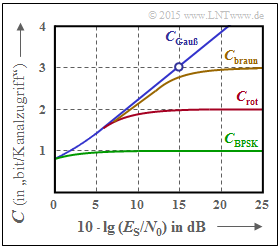
P ID2952 Inf A 4 9.png

Die Grafik zeigt AWGN–Kanalkapazitätskurven über der Abszisse 10 · lg (ES/N0):

  • CGauß:   Shannonsche Grenzkurve,
  • CBPSK:   gültig für BPSK.

Die beiden weiteren Kurvenverläufe Crot und Cbraun sollen in den Teilaufgaben (c) und (d) analysiert und möglichen Modulationsverfahren zugeordnet werden.


Hinweis

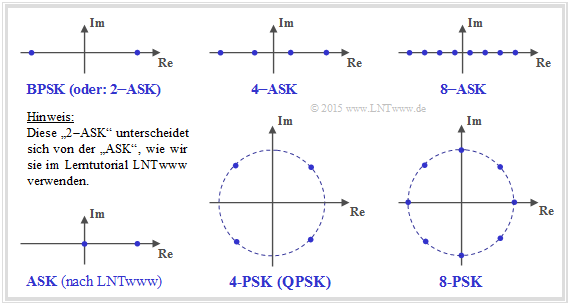
Die hier genannten Modulationsverfahren werden anhand ihrer Signalraumkonstellation beschrieben:

P ID2953 Inf A 4 9 Zusatz.png

In der Literatur wird manchmal die BPSK auch mit 2–ASK bezeichnet ⇒ x ∈ X = (+1, –1). Dagegen verstehen wir im LNTwww als ASK den unipolaren Fall x ∈ X = (0, 1). Nach unserer Nomenklatur gilt deshalb: CASK < CBPSK.
Dieser Sachverhalt hat aber keinen Einfluss auf die Lösung der vorliegenden Aufgabe.


Fragebogen

1

Welche Gleichung liegt der Shannon–Grenzkurve CGauß zugrunde?

Es gilt CGauß = C1 = 1/2 · log2 (1 + ES/N0),
Es gilt CGauß = C2 = 1/2 · log2 (1 + 2ES/N0),
Es gilt CGauß = C3 = log2 (1 + ES/N0).

2

Welche Aussagen treffen für die grüne Kurve CBPSK zu?

CBPSK kann nicht in geschlossener Form angegeben werden.
CBPSK ist größer als 0, wenn ES/N0 > 0 vorausgesetzt wird.
Für ES/N0 < ln (2) ist CBPSK ≡ 0.
Im gesamten Bereich gilt CBPSK < CGauß.

3

Welche Aussagen treffen für die rote Kurve zu?

Für die zugehörige Zufallsgröße X gilt MX = |X| = 2.
Für die zugehörige Zufallsgröße X gilt MX = |X| = 4.
Crot ist gleichzeitig die Kanalkapazität der 4–ASK.
Crot ist gleichzeitig die Kanalkapazität der 4–QAM.
Für alle ES/N0 > 0 liegt Crot zwischen „grün” und „braun”.

4

Welche Aussagen treffen für die braune Kurve zu?

Für die zugehörige Zufallsgröße gilt MX = |X| = 8.
Cbraun ist gleichzeitig die Kanalkapazität der 8–ASK.
Cbraun ist gleichzeitig die Kanalkapazität der 8–PSK..
pB = 0 ist mit 8–ASK, R = 2.5 und (ES/N0)dB = 10 dB möglich.
pB = 0 ist mit 8–ASK, R = 2 und (ES/N0)dB = 10 dB möglich.


Musterlösung

Musterlösung

1. 2. 3. 4. 5. 6. 7.

Abgerufen von „http://www.lntwww.de/index.php?title=Aufgaben:Aufgabe_4.9:_Höherstufige_Modulation&oldid=12142“
  • Powered by MediaWiki