Digitalsignalübertragung/Grundlagen der codierten Übertragung: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
| + | |||
| + | Das zweite Kapitel behandelt die so genannte '''Übertragungscodierung''', die in der Literatur manchmal auch als „Leitungscodierung” bezeichnet wird. Dabei wird durch gezieltes Hinzufügen von Redundanz eine Anpassung des digitalen Sendesignals an die Eigenschaften des Übertragungskanals erreicht. Im Einzelnen werden behandelt: | ||
| + | |||
| + | *einige grundlegende Begriffe der Informationstheorie wie ''Informationsgehalt'' und ''Entropie'', | ||
| + | *die AKF-Berechnung und die Leistungsdichtespektren von Digitalsignalen, | ||
| + | *die redundanzfreie Codierung, die zu einem nichtbinären Sendesignal führt, | ||
| + | *die Berechnung von Symbol- und Bitfehlerwahrscheinlichkeit bei mehrstufigen Systemen, | ||
| + | *die so genannten 4B3T-Codes als ein wichtiges Beispiel von blockweiser Codierung, und | ||
| + | *die Pseudoternärcodes, die jeweils eine symbolweise Codierung realisieren. | ||
| + | |||
| + | Die Beschreibung erfolgt durchgehend im Basisband und es werden weiterhin einige vereinfachende Annahmen (unter Anderem: keine Impulsinterferenzen) getroffen. | ||
| + | |||
| + | Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im | ||
| + | |||
| + | Kapitel 15: Lineare zeitinvariante Systeme, Programm lzi | ||
| + | |||
| + | des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf | ||
| + | |||
| + | *dem Lehrsoftwarepaket [http://www.lntwww.de/downloads/Sonstiges/Programme/LNTsim.zip LNTsim] ⇒ Link verweist auf die ZIP-Version des Programms und | ||
| + | *dieser [http://www.lntwww.de/downloads/Sonstiges/Texte/Praktikum_LNTsim_Teil_B.pdf Praktikumsanleitung] ⇒ Link verweist auf die PDF-Version; Kapitel 15: Seite 99-118. | ||
== Informationsgehalt – Entropie – Redundanz == | == Informationsgehalt – Entropie – Redundanz == | ||
Version vom 22. August 2017, 08:54 Uhr
Das zweite Kapitel behandelt die so genannte Übertragungscodierung, die in der Literatur manchmal auch als „Leitungscodierung” bezeichnet wird. Dabei wird durch gezieltes Hinzufügen von Redundanz eine Anpassung des digitalen Sendesignals an die Eigenschaften des Übertragungskanals erreicht. Im Einzelnen werden behandelt:
- einige grundlegende Begriffe der Informationstheorie wie Informationsgehalt und Entropie,
- die AKF-Berechnung und die Leistungsdichtespektren von Digitalsignalen,
- die redundanzfreie Codierung, die zu einem nichtbinären Sendesignal führt,
- die Berechnung von Symbol- und Bitfehlerwahrscheinlichkeit bei mehrstufigen Systemen,
- die so genannten 4B3T-Codes als ein wichtiges Beispiel von blockweiser Codierung, und
- die Pseudoternärcodes, die jeweils eine symbolweise Codierung realisieren.
Die Beschreibung erfolgt durchgehend im Basisband und es werden weiterhin einige vereinfachende Annahmen (unter Anderem: keine Impulsinterferenzen) getroffen.
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
Kapitel 15: Lineare zeitinvariante Systeme, Programm lzi
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms und
- dieser Praktikumsanleitung ⇒ Link verweist auf die PDF-Version; Kapitel 15: Seite 99-118.
Inhaltsverzeichnis
Informationsgehalt – Entropie – Redundanz
Wir gehen von einer M–stufigen digitalen Nachrichtenquelle aus, die das Quellensignal
\(q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)\hspace{0.3cm}{\rm mit}\hspace{0.3cm}a_\nu \in \{ a_1, ... , a_\mu , ... , a_{ M}\}\)
abgibt. Die Quellensymbolfolge 〈qν〉 ist auf die Folge 〈aν〉 der dimensionslosen Amplitudenkoeffizienten abgebildet. Vereinfachend wird zunächst für die Zeitlaufvariable ν = 1, ... , N gesetzt, während der Vorratsindex μ stets Werte zwischen 1 und M annehmen kann.
Ist das ν–te Folgenelement gleich aμ, so kann dessen Informationsgehalt mit der Wahrscheinlichkeit pνμ = Pr(aν = aμ) wie folgt berechnet werden:
- \[I_\nu = \log_2 \frac{1}{p_{\nu \mu}}= {\rm ld} \frac{1}{p_{\nu \mu}} \hspace{1cm}{\rm (Einheit: \hspace{0.15cm}bit)}\hspace{0.05cm}.\]
Der Logarithmus zur Basis 2 ⇒ log2 wird oft auch mit „ld(x)” ⇒ Logarithmus dualis bezeichnet. Bei der numerischen Auswertung wird die Hinweiseinheit „bit” hinzugefügt. Mit dem Zehner-Logarithmus lg(x) bzw. dem natürlichen Logarithmus ln(x) gilt:
\[{\rm log_2}(x) = \frac{{\rm lg}(x)}{{\rm lg}(2)}= \frac{{\rm ln}(x)}{{\rm ln}(2)}\hspace{0.05cm}.\]
Nach dieser auf C. E. Shannon zurückgehenden Definition von Information ist der Informationsgehalt eines Symbols umso größer, je kleiner dessen Auftrittswahrscheinlichkeit ist.
\[H = \lim_{N \to \infty} \frac{1}{N} \cdot \sum_{\nu = 1}^N I_\nu =
\lim_{N \to \infty} \frac{1}{N} \cdot \sum_{\nu = 1}^N \hspace{0.1cm}{\rm log_2}\hspace{0.05cm} \frac{1}{p_{\nu \mu}} \hspace{1cm}{\rm (Einheit: \hspace{0.15cm}bit)}\hspace{0.05cm}.\]
Natürlich kann die Entropie auch durch Scharmittelung berechnet werden.
Sind die Folgenelemente aν statistisch voneinander unabhängig, so sind die Auftrittswahrscheinlichkeiten pνμ = pμ unabhängig von ν und man erhält in diesem Sonderfall für die Entropie:
\[H = \sum_{\mu = 1}^M p_{ \mu} \cdot {\rm log_2}\hspace{0.1cm} \frac{1}{p_{ \mu}}\hspace{0.05cm}.\]
Bestehen dagegen statistische Bindungen zwischen benachbarten Amplitudenkoeffizienten aν, so muss zur Entropieberechnung die kompliziertere Definitionsgleichung herangezogen werden.
Der Maximalwert der Entropie ergibt sich immer dann, wenn die M Auftrittswahrscheinlichkeiten (der statistisch unabhängigen Symbole) alle gleich sind (pμ = 1/M):
\(H_{\rm max} = \sum_{\mu = 1}^M \hspace{0.1cm}\frac{1}{M} \cdot {\rm log_2} (M) = {\rm log_2} (M) \cdot \sum_{\mu = 1}^M \hspace{0.1cm} \frac{1}{M} = {\rm log_2} (M)
\hspace{1cm}{\rm (Einheit: \hspace{0.15cm}bit)}\hspace{0.05cm}.\)
Man bezeichnet Hmax als den Entscheidungsgehalt (bzw. als Nachrichtengehalt) und den Quotienten
\(r = \frac{H_{\rm max}-H}{H_{\rm max}}\)
als dierelative Redundanz. Da stets 0 ≤ H ≤ Hmax gilt, kann die relative Redundanz Werte zwischen 0 und 1 (einschließlich dieser Grenzwerte) annehmen.
Aus der Herleitung dieser Beschreibungsgrößen ist offensichtlich, dass ein redundanzfreies Digitalsignal (r = 0) folgende Eigenschaften erfüllen muss:
- Die Amplitudenkoeffizienten aν sind statistisch unabhängig; Pr(aν = aμ) ist für alle ν identisch.
- Die M möglichen Koeffizienten aμ treten mit gleicher Wahrscheinlichkeit pμ = 1/M auf.
- der unterschiedlichen Häufigkeiten (beispielsweise tritt „e” deutlich häufiger auf als „u”) und
- von statistischen Bindungen (zum Beispiel folgt auf „q” der Buchstabe „u” viel öfters als „e”)
beträgt nach Karl Küpfmüller die Entropie der deutschen Sprache nur H = 1.3 bit/Zeichen. Daraus ergibt sich die relative Redundanz zu r ≈ (5 – 1.3)/5 = 74%. Für englische Texte wurde von Claude E. Shannon die Entropie mit H = 1 bit/Zeichen angegeben (r = 80%).
Quellen–, Kanal– und Übertragungscodierung
Unter Codierung versteht man die Umsetzung der Quellensymbolfolge 〈qν〉 mit Symbolumfang Mq in eine Codesymbolfolge 〈cν〉 mit dem Symbolumfang Mc. Meist wird durch die Codierung die in einem Digitalsignal enthaltene Redundanz manipuliert. Oft – aber nicht immer – sind Mq und Mc verschieden.
Man unterscheidet je nach Zielrichtung zwischen verschiedenen Arten von Codierung:
- Die Aufgabe der Quellencodierung ist die Redundanzreduktion zur Datenkomprimierung, wie sie beispielsweise in der Bildcodierung Anwendung findet. Durch Ausnutzung statistischer Bindungen zwischen den einzelnen Punkten eines Bildes bzw. zwischen den Helligkeitswerten eines Punktes zu verschiedenen Zeiten (bei Bewegtbildsequenzen) können Verfahren entwickelt werden, die bei nahezu gleicher Bildqualität zu einer merklichen Verminderung der Datenmenge (gemessen in bit oder byte) führen. Ein einfaches Beispiel hierfür ist die differentielle Pulscodemodulation (DPCM).
- Bei der Kanalcodierung erzielt man demgegenüber dadurch eine merkliche Verbesserung des Übertragungsverhaltens, dass eine beim Sender gezielt hinzugefügte Redundanz empfangsseitig zur Erkennung und Korrektur von Übertragungsfehlern genutzt wird. Solche Codes, deren wichtigste Vertreter Block–, Faltungs– und Turbo-Codes sind, haben besonders bei stark gestörten Kanälen eine große Bedeutung. Je größer die relative Redundanz des codierten Signals ist, desto besser sind die Korrektureigenschaften des Codes, allerdings bei verringerter Nutzdatenrate.
- Eine Übertragungscodierung – häufig auch als Leitungscodierung bezeichnet – verwendet man, um das Sendesignal durch eine Umcodierung der Quellensymbole an die spektralen Eigenschaften von Übertragungskanal und Empfangseinrichtungen anzupassen. Beispielsweise muss bei einem Kanal mit der Frequenzgangseigenschaft HK(f = 0) = 0, über den kein Gleichsignal übertragen werden kann, durch Übertragungscodierung sichergestellt werden, dass die Codesymbolfolge weder eine lange L– noch eine lange H–Folge beinhaltet.
Im vorliegenden Buch „Digitalsignalübertragung” beschäftigen wir uns ausschließlich mit diesem letzten, übertragungstechnischen Aspekt. Der Kanalcodierung ist in LNTwww ein eigenes Buch gewidmet (siehe Bücherregalseite), während die Quellencodierung im Buch „Informationstheorie” ausführlich behandelt wird. Auch die Sprachcodierung im Kapitel 3.3 des Buches „Beispiele von Nachrichtensystemen” stellt eine spezielle Form der Quellencodierung dar.
Systemmodell und Beschreibungsgrößen
Im weiteren Verlauf des zweiten Kapitels wird von folgendem Blockschaltbild ausgegangen.
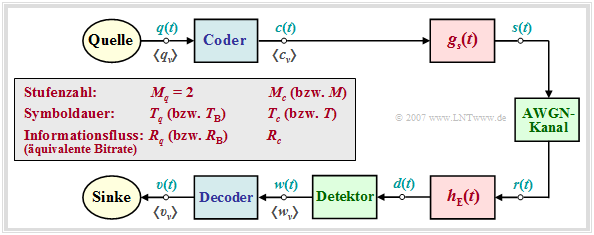
Zusätzlich gelten folgende Vereinbarungen:
- Das digitale Quellensignal q(t) sei binär (Mq = 2) und redundanzfrei (Hq = 1 bit/Symbol). Mit der Symboldauer Tq ergibt sich für die Symbolrate der Quelle:
- \[R_q = {H_{q}}/{T_q}= {1}/{T_q}\hspace{1cm}{\rm (Einheit: \hspace{0.15cm}bit/s)}\hspace{0.05cm}.\]
- Wegen Mq = 2 bezeichnen wir im Folgenden Tq auch als die Bitdauer und Rq als die Bitrate. Für den Vergleich von Übertragungssystemen mit unterschiedlicher Codierung werden Tq und Rq (in späteren Kapiteln verwenden wir hierfür TB und RB) stets als konstant angenommen.
- Das Codersignal c(t) und auch das Sendesignal s(t) nach der Impulsformung mit gs(t) besitzen die Stufenzahl Mc, die Symboldauer Tc und die Symbolrate 1/Tc. Die äquivalente Bitrate beträgt
- \[R_c = {{\rm log_2} (M_c)}/{T_c} \hspace{0.05cm}.\]
- Es gilt stets Rc ≥ Rq, wobei das Gleichheitszeichen nur bei den redundanzfreien Codes (rc = 0) gültig ist. Andernfalls erhält man für die relative Coderedundanz:
- \[r_c =({R_c - R_q})/{R_c} = 1 - R_q/{R_c} \hspace{0.05cm}.\]
Hinweis zur Nomenklatur: Die äquivalente Bitrate Rc des Codersignals hat ebenso wie die Bitrate Rq der Quelle die Einheit „bit/s”. Insbesondere in der Literatur zur Kanalcodierung wird dagegen mit Rc häufig die dimensionslose Coderate 1 – rc bezeichnet. Rc = 1 gibt dann einen redundanzfreien Code an, während Rc = 1/3 einen Code mit der Redundanz rc = 2/3 kennzeichnet.
\[R_q = {1}/{T_q}, \hspace{-0.05cm}R_c = {{\rm log_2} (3)} \hspace{-0.05cm}/{T_c} = {3/4 \cdot {\rm log_2} (3)} \hspace{-0.05cm}/{T_q}\hspace{0.1cm}\Rightarrow \hspace{0.1cm}r_c =3/4\cdot {\rm log_2} (3) \hspace{-0.05cm}- \hspace{-0.05cm}1 \approx 15.9\, \% \hspace{0.05cm}.\]
Genauere Informationen zu den 4B3T-Codes finden Sie im Kapitel 2.3.
AKF–Berechnung eines Digitalsignals
Zur Vereinfachung der Schreibweise wird im Folgenden Mc = M und Tc = T gesetzt. Damit kann für das Sendesignal bei einer zeitlich unbegrenzten Nachrichtenfolge geschrieben werden:
\[s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.\]
Diese Signaldarstellung beinhaltet sowohl die Quellenstatistik (Amplitudenkoeffizienten aν) als auch die Sendeimpulsform gs(t).
Die Grafik zeigt zwei binäre bipolare Sendesignale sG(t) und sR(t) mit gleichen Amplitudenkoeffizienten aν, die sich lediglich durch den Sendegrundimpuls gs(t) unterscheiden.
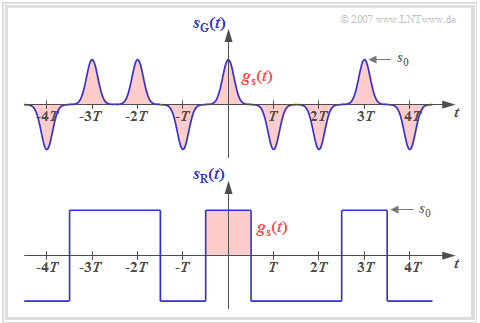
Man erkennt aus dieser Darstellung, dass ein Digitalsignal im Allgemeinen nichtstationär ist:
- Beim Sendesignal sG(t) mit schmalen Gaußimpulsen ist die Nichtstationarität offensichtlich, da zum Beispiel bei Vielfachen von T die Varianz σs2 = s02 ist, während dazwischen σs2 ≈ 0 gilt.
- Auch das Signal sR(t) mit NRZ–rechteckförmigen Impulsen ist im strengen Sinne nichtstationär, da sich hier die Momente an den Bitgrenzen gegenüber allen anderen Zeitpunkten unterscheiden.
- Einen Zufallsprozess, dessen Momente mk(t) = mk(t + ν · T) sich periodisch mit T wiederholen, bezeichnet man als zyklostationär; k und ν besitzen hierbei ganzzahlige Zahlenwerte.
Viele der für ergodische Prozesse gültigen Regeln kann man mit nur geringen Einschränkungen auch auf zykloergodische (und damit ebenfalls auf zyklostationäre) Prozesse anwenden. Insbesondere gilt für die Autokorrelationsfunktion (AKF) solcher Zufallsprozesse mit Mustersignal s(t):
\[\varphi_s(\tau) = {\rm E}[s(t) \cdot s(t + \tau)] \hspace{0.05cm}.\]
Mit obiger Gleichung des Sendesignals kann die AKF als Zeitmittelwert wie folgt geschrieben werden:
\[\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}\frac{1}{T}
\cdot \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu =
-N}^{+N} a_\nu \cdot a_{\nu + \lambda} \cdot
\int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau -
\lambda \cdot T)\,{\rm d} t \hspace{0.05cm}.\]
Wir gehen weiterhin von folgender AKF–Gleichung aus:
\(\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}\frac{1}{T}
\cdot \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu =
-N}^{+N} a_\nu \cdot a_{\nu + \lambda} \cdot
\int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau -
\lambda \cdot T)\,{\rm d} t \hspace{0.05cm}.\)
Da die Grenzwert–, Integral– und Summenbildung miteinander vertauscht werden darf, kann mit den Substitutionen N = TM/(2T),
λ = κ – ν und t – ν · T → t hierfür auch geschrieben werden:
\(\varphi_s(\tau) = \lim_{T_{\rm M} \to \infty}\frac{1}{T_{\rm M}}
\cdot
\int_{-T_{\rm M}/2}^{+T_{\rm M}/2}
\sum_{\nu = -\infty}^{+\infty} \sum_{\kappa = -\infty}^{+\infty}
a_\nu \cdot g_s ( t - \nu \cdot T ) \cdot
a_\kappa \cdot g_s ( t + \tau - \kappa \cdot T )
\,{\rm d} t \hspace{0.05cm}.\)
Nun werden zur Abkürzung folgende Größen eingeführt:
Das Signal s(t) kann dabei binär oder mehrstufig, unipolar oder bipolar sowie redundanzfrei oder redundant (leitungscodiert) sein. Die Impulsform wird durch die Energie–AKF berücksichtigt.
Beschreibt das Digitalsignal s(t) einen Spannungsverlauf, so hat die Energie–AKF des Grundimpulses gs(t) die Einheit V2s und φs(τ) die Einheit V2, jeweils bezogen auf den Widerstand 1 Ω.
Anmerkung: Im strengen Sinne der Systemtheorie müsste man die AKF der Amplitudenkoeffizienten wie folgt definieren:
\(\varphi_{a , \delta}(\tau) = \sum_{\lambda = -\infty}^{+\infty}
\varphi_a(\lambda)\cdot \delta(\tau - \lambda \cdot
T)\hspace{0.05cm}.\)
Damit würde sich die obige Gleichung wie folgt darstellen:
\(\varphi_s(\tau) ={1}/{T} \cdot \varphi_{a ,
\delta}(\tau)\star \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot
T) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot
\varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda
\cdot T)\hspace{0.05cm}.\)
Zur einfacheren Darstellung wird im Folgenden die diskrete AKF der Amplitudenkoeffizienten
⇒ φa(λ)
stets ohne diese Diracfunktionen verwendet.
LDS–Berechnung eines Digitalsignals
Die Entsprechungsgröße zur Autokorrelationsfunktion (AKF) eines Zufallssignals ist im Frequenzbereich das Leistungsdichtespektrum (LDS), das mit der AKF über das Fourierintegral in Bezug steht:
\(\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm}
{\it \Phi}_s(f) = \int\limits_{-\infty}^{+\infty} \varphi_s(\tau) \cdot
{\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau}
\,{\rm d} \tau \hspace{0.05cm}.\)
Berücksichtigt man den Zusammenhang zwischen Energie–AKF und Energiespektrum,
\(\varphi^{^{\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm}
{\it \Phi}^{^{\bullet}}_{gs}(f) = |G_s(f)|^2
\hspace{0.05cm},\)
sowie den Verschiebungssatz, so kann das Leistungsdichtespektrum des Digitalsignals s(t) in folgender Weise dargestellt werden:
\({\it \Phi}_s(f) = \sum_{\lambda =
-\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot {\it
\Phi}^{^{\bullet}}_{gs}(f) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}
2 \pi f \hspace{0.02cm} \lambda T} = \)
- \[ = {1}/{T} \cdot |G_s(f)|^2 \cdot \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot \cos ( 2 \pi f \lambda T)\hspace{0.05cm}.\]
Hierbei ist berücksichtigt, dass Φs(f) und |Gs(f)|2 reellwertig sind und gleichzeitig φa(– λ) = φa(λ) gilt.
Definiert man nun die spektrale Leistungsdichte der Amplitudenkoeffizienten zu
\({\it \Phi}_a(f) = \sum_{\lambda =
-\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm
j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda \hspace{0.02cm}T} =
\varphi_a(0) + 2 \cdot \sum_{\lambda =
1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f
\lambda T) \hspace{0.05cm},\)
so erhält man den folgenden Ausdruck:
\({\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot
|G_s(f)|^2 \hspace{0.05cm}.\)
Das heißt, dass sich Φs(f) als Produkt zweier Funktionen darstellen lässt:
- Der erste Term Φa(f) ist dimensionslos und beschreibt die spektrale Formung des Sendesignals durch die statistischen Bindungen der Quelle.
- Dagegen berücksichtigt |Gs(f)|2 die spektrale Formung durch den Sendegrundimpuls gs(t). Je schmaler dieser ist, desto breiter ist |Gs(f)|2 und um so größer ist damit der Bandbreitenbedarf.
- Das Energiespektrum hat die Einheit V2s/Hz. Die Einheit V2/Hz für das Leistungsdichtespektrum (nur gültig für den Widerstand 1 Ω) ergibt sich aufgrund der Division durch den Symbolabstand T.
AKF und LDS bei bipolaren Binärsignalen
Die bisherigen Ergebnisse werden nun an Beispielen verdeutlicht. Ausgehend von binären bipolaren Amplitudenkoeffizienten aν ∈ {–1, +1} erhält man, falls keine Bindungen zwischen den aν bestehen:
\(\varphi_a(\lambda) = \left\{ \begin{array}{c} 1
\\ 0 \\ \end{array} \right.\quad
\begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array}
\begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \\
\end{array}
\hspace{0.5cm}\Rightarrow \hspace{0.5cm}\varphi_s(\tau)=
{1}/{T} \cdot \varphi^{^{\bullet}}_{gs}(\tau)\hspace{0.05cm}.\)
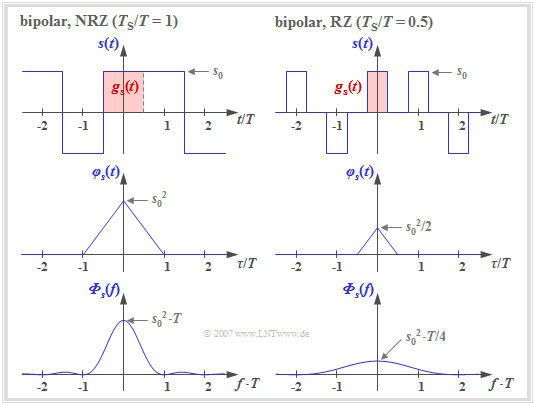
Die Grafik zeigt zwei Signalausschnitte jeweils mit Rechteckimpulsen gs(t), die dementsprechend zu einer dreieckförmigen AKF und zu einem si2–förmigen Leistungsdichtespektrum (LDS) führen.
Die linken Bilder beschreiben eine NRZ–Signalisierung, das heißt, dass die Breite TS des Grundimpulses gleich dem Abstand T zweier Sendeimpulse (Quellensymbole) ist. Dagegen gelten die rechten Bilder für einen RZ–Impuls mit dem Tastverhältnis TS/T = 0.5. Man erkennt:
- Bei NRZ–Rechteckimpulsen ergibt sich für die (auf den Widerstand 1 Ω bezogene) Sendeleistung φs(τ = 0) = s02 und die dreieckförmige AKF ist auf den Bereich |τ| ≤ TS = T beschränkt.
- Das LDS Φs(f) als die Fouriertransformierte von φs(τ) ist si2–förmig mit äquidistanten Nullstellen im Abstand 1/T. Die Fläche unter der LDS–Kurve ergibt wiederum die Sendeleistung s02.
- Im Fall der RZ–Signalisierung ist die dreieckförmige AKF gegenüber dem linken Bild in Höhe und Breite jeweils um den Faktor TS/T = 0.5 kleiner.
Vergleicht man die beiden Leistungsdichtespektren (untere Bilder), so erkennt man für TS/T = 0.5 gegenüber TS/T = 1 eine Verkleinerung in der Höhe um den Faktor 4 und eine Verbreiterung um den Faktor 2. Die Fläche (Leistung) ist somit halb so groß, da in der Hälfte der Zeit s(t) = 0 gilt.
AKF und LDS bei unipolaren Binärsignalen
Wir gehen weiterhin von NRZ– bzw. RZ–Rechteckimpulsen aus. Die binären Amplitudenkoeffizienten seien aber nun unipolar: aν ∈ {0, 1}. Dann gilt für die diskrete AKF der Amplitudenkoeffizienten\[\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 = 0.5 \\
\\ m_1^2 = 0.25 \\ \end{array} \right.\quad
\begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ {\rm{f\ddot{u}r}} \\ \end{array}
\begin{array}{*{20}c}\lambda = 0, \\ \\ \lambda \ne 0 \hspace{0.05cm}.\\
\end{array}\]
Vorausgesetzt sind hier gleichwahrscheinliche Amplitudenkoeffizienten
⇒ Pr(aν = 0) = Pr(aν = 1) = 0.5
ohne statistische Bindungen untereinander, so dass sowohl der quadratische Mittelwert m2 als auch der lineare Mittelwert m1 jeweils gleich 0.5 sind.
Hinweis: Unipolare Amplitudenkoeffizienten treten zum Beispiel bei optischen Übertragungssystemen auf. Trotzdem beschränken wir uns in späteren Kapiteln meist auf die bipolare Signalisierung.
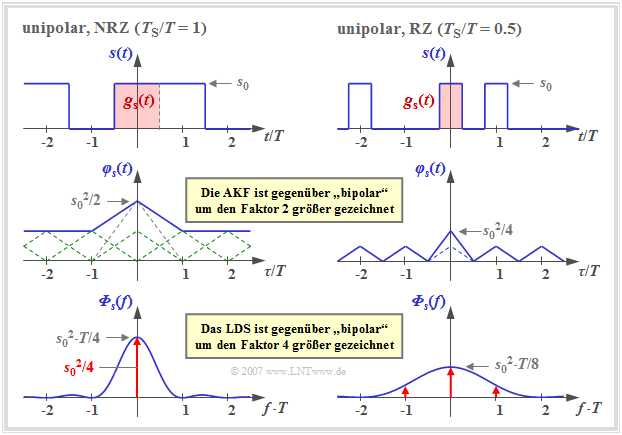
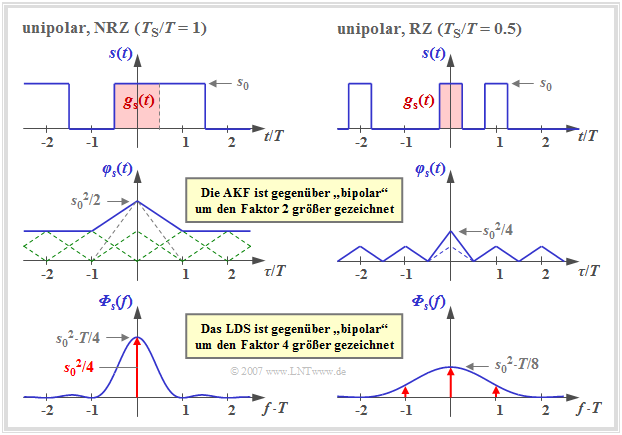
Die Grafik zeigt einen Signalausschnitt, die AKF und das LDS mit unipolaren Amplitudenkoeffizienten,
- links für rechteckförmige NRZ–Impulse (TS/T = 1), und
- rechts für RZ–Impulse mit dem Tastverhältnis TS/T = 0.5.
Man erkennt folgende Unterschiede gegenüber der bipolaren Signalisierung:
- Durch die Addition der unendlich vielen Dreieckfunktionen im Abstand T, alle mit gleicher Höhe, ergibt sich für die AKF in der linken Grafik (NRZ) ein konstanter Gleichanteil s02/4.
- Daneben verbleibt im Bereich |τ| ≤ TS eine einzelne Dreieckfunktion mit der Höhe s02/4, die im Leistungsdichtespektrum (LDS) zum kontinuierlichen, si2–förmigen Verlauf führt (blaue Kurve).
- Der Gleichanteil in der AKF bewirkt im LDS eine Diracfunktion bei der Frequenz f = 0 mit dem Gewicht s02/4. Es ist zu bemerken, dass dadurch der LDS–Wert Φs(f = 0) unendlich groß wird.
- Aus der rechten Grafik – gültig für TS/T = 0.5 – erkennt man, dass sich nun die AKF aus einem periodischen Dreiecksverlauf (im mittleren Bereich gestrichelt eingezeichnet) und zusätzlich noch aus einem einmaligen Dreieck im Bereich |τ| ≤ TS = T/2 mit Höhe s02/8 zusammensetzt.
- Diese einmalige Dreieckfunktion führt zu dem kontinuierlichen, si2–förmigen Anteil (blaue Kurve) von Φs(f) mit der ersten Nullstelle bei 1/TS = 2/T. Dagegen führt die periodische Dreieckfunktion nach den Gesetzmäßigkeiten der Fourierreihe zu einer unendlichen Summe von Diracfunktionen mit unterschiedlichen Gewichten im Abstand 1/T (rot gezeichnet).
- Die Gewichte der Diracfunktionen sind proportional zum kontinuierlichen (blauen) LDS–Anteil. Das maximale Gewicht s02/8 besitzt die Diraclinie bei f = 0. Dagegen sind die Diraclinien bei ±2/T und Vielfachen davon nicht vorhanden bzw. besitzen jeweils das Gewicht 0, da hier auch der kontinuierliche LDS–Anteil Nullstellen besitzt.
Aufgaben
A2.1 AKF und LDS nach Codierung
Zusatzaufgaben:2.1 Zur äquivalenten Bitrate
A2.2 Binäre bipolare Rechtecke