Aufgaben:Aufgabe 3.14: Kanalcodierungstheorem: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 3.13 Kanalcodierungstheorem nach 3.14 Kanalcodierungstheorem) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
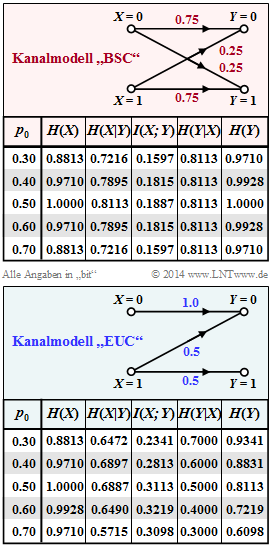
| − | [[Datei:P_ID2817__Inf_A_3_13.png|right|]] | + | [[Datei:P_ID2817__Inf_A_3_13.png|right|frame|Informationstheoretische Größen von BSC– und EUC–Modell]] |
| − | Shannons Kanalcodierungstheorem besagt, dass über einen diskreten gedächtnislosen Kanal (DMC) mit der Coderate $R$ fehlerfrei übertragen werden kann, so lange $R$ nicht größer ist als die Kanalkapazität | + | [https://de.wikipedia.org/wiki/Claude_Shannon Shannons] Kanalcodierungstheorem besagt, dass über einen ''diskreten gedächtnislosen Kanal'' (englisch: ''Discrete Memoryless Channel'', DMC) mit der Coderate $R$ fehlerfrei übertragen werden kann, so lange $R$ nicht größer ist als die Kanalkapazität |
| − | $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ | + | :$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ |
Das Kanalcodierungstheorem soll in dieser Aufgabe numerisch ausgewertet werden, wobei zwei typische Kanalmodelle zu betrachten sind: | Das Kanalcodierungstheorem soll in dieser Aufgabe numerisch ausgewertet werden, wobei zwei typische Kanalmodelle zu betrachten sind: | ||
| − | :* das | + | :* das '''BSC–Modell''' ''(Binary Symmetric Channel)'' mit Verfälschungswahrscheinlichkeit $ε = 0.25$ und der Kanalkapazität $C = 1 – H_{\rm bin}(ε),$ |
| − | :* das sog. | + | :* das sog. '''EUC–Modell''' (von ''Extremely Unsymmetric Channel'', diese Bezeichnung ist nicht allgemein üblich) entsprechend der [[Aufgaben:3.10Z_Extrem_unsymmetrischer_Kanal|Zusatzaufgabe 3.11Z]]. |
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung|Anwendung auf die Digitalsignalübertragung]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Rate.2C_Kanalkapazit.C3.A4t_und_Bitfehlerwahrscheinlichkeit|Rate, Kanalkapazität und Bitfehlerwahrscheinlichkeit]]. | ||
| + | *Die Werte der binären Entropiefunktion werden zum Beispiel durch das interaktice Berechnungsmodul [[Entropien von Nachrichtenquellen]] bereitgestellt. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
'''Hinweis:''' Diese Aufgabe gehört zum Themengebiet von [http://www.lntwww.de/Informationstheorie/Anwendung_auf_die_Digitalsignal%C3%BCbertragung Kapitel 3.3]. Die Grafiken zeigen die numerischen Werte der informationstheoretischen Größen für die beiden Kanäle „BSC” und „EUC”: | '''Hinweis:''' Diese Aufgabe gehört zum Themengebiet von [http://www.lntwww.de/Informationstheorie/Anwendung_auf_die_Digitalsignal%C3%BCbertragung Kapitel 3.3]. Die Grafiken zeigen die numerischen Werte der informationstheoretischen Größen für die beiden Kanäle „BSC” und „EUC”: | ||
Version vom 7. Juni 2017, 17:13 Uhr
Shannons Kanalcodierungstheorem besagt, dass über einen diskreten gedächtnislosen Kanal (englisch: Discrete Memoryless Channel, DMC) mit der Coderate $R$ fehlerfrei übertragen werden kann, so lange $R$ nicht größer ist als die Kanalkapazität
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
Das Kanalcodierungstheorem soll in dieser Aufgabe numerisch ausgewertet werden, wobei zwei typische Kanalmodelle zu betrachten sind:
- das BSC–Modell (Binary Symmetric Channel) mit Verfälschungswahrscheinlichkeit $ε = 0.25$ und der Kanalkapazität $C = 1 – H_{\rm bin}(ε),$
- das sog. EUC–Modell (von Extremely Unsymmetric Channel, diese Bezeichnung ist nicht allgemein üblich) entsprechend der Zusatzaufgabe 3.11Z.
Hinweise:
- Die Aufgabe gehört zum Kapitel Anwendung auf die Digitalsignalübertragung.
- Bezug genommen wird insbesondere auf die Seite Rate, Kanalkapazität und Bitfehlerwahrscheinlichkeit.
- Die Werte der binären Entropiefunktion werden zum Beispiel durch das interaktice Berechnungsmodul Entropien von Nachrichtenquellen bereitgestellt.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Hinweis: Diese Aufgabe gehört zum Themengebiet von Kapitel 3.3. Die Grafiken zeigen die numerischen Werte der informationstheoretischen Größen für die beiden Kanäle „BSC” und „EUC”:
- der Quellenentropie $H(X),$
- der Äquivokation $H(X|Y),$
- der Transinformation $I(X; Y),$
- der Irrelevanz $H(Y|X),$ und
- der Sinkenentropie $H(Y).$
Der Parameter in diesen Tabellen ist $p_0 = Pr(X = 0)$ im Bereich von $0.3$ bis $0.7.$ Entsprechend gilt für die Wahrscheinlichkeit des Quellensymbols „1”: $p_1 = 1 – p_0$
Fragebogen
Musterlösung
2. Beim BSC–Modell mit der Verfälschungswahrscheinlichkeit $ε = 0.25$ gilt bei uncodierter Übertragung $(R = 1)$ unabhängig von $p_0$ und $p_1$ für die Bitfehlerwahrscheinlichkeit: $p_B = 0.25$. Dagegen erhält man beim EUC–Modell beispielsweise mit $p_0 = 0.6$ und $p_1 = 0.4$ eine kleinere Bitfehlerwahrscheinlichkeit: $$p_{\rm B} = 0.6 \cdot 0 + 0.4 \cdot 0.5=0.2 \hspace{0.05cm}.$$ Richtig ist demnach der Lösungsvorschlag 3.
Zu beachten ist jedoch, dass nun die Quellenentropie nicht mehr $H(X) = 1 (bit)$ beträgt, sondern nur mehr $H(X) = H_{bin} (0.6) = 0.971 (bit)$. Im Grenzfall $p_0 = 1$ werden nur noch Nullen übertragen und es gilt $H(X) = 0$. Für die Bitfehlerwahrscheinlichkeit gilt dann aber tatsächlich: $$ p_{\rm B} = 1 \cdot 0 + 0 \cdot 0.5=0 \hspace{0.05cm}.$$ Man überträgt also keine Information, diese aber mit der Bitfehlerwahrscheinlichkeit $0$
3.Aus der Grafik auf der Angabenseite lässt sich für die Kapazitäten der beiden Kanäle ablesen:
- $C_{BSC} = 0.1887 bit/use,$
- $C_{EUC} = 0.3219 bit/use.$
Nach dem Kanalcodierungstheorem kann unter der Bedingung $R ≤ C$ eine Kanalcodierung gefunden werden, mit der die Fehlerwahrscheinlichkeit zu $0$ gemacht werden kann. Bei beiden Kanälen trifft dies mit $R = 0.16$ zu $⇒$ Lösungsvorschlag 1.
4. Richtig ist hier der Lösungsvorschlag 3: Beim EUC–Modell wird mit $R = 0.32$ und $C = 0.3219$ die notwendige Bedingung $R ≤ C$ für eine fehlerfreie Übertragung erfüllt. Voraussetzung hierfür ist allerdings die Wahrscheinlichkeitsfunktion $P_X(X) = (0.6, 0.4).$ Dagegen ergäbe sich für gleichwahrscheinliche Symbole $ ⇒ P_X(X) = (0.5, 0.5)$ die Transinformation $I(X; Y) = 0.3113 < R.$
Man erkennt: Das EUC–Modell bietet mehr Potenzial für die Anwendung einer Kanalcodierung als das BSC–Modell. Hier kann beispielsweise im Code ausgenutzt werden, dass eine gesendete „0” stets fehlerfrei übertragen wird.
5. Aus der Kommentierung der Aufgaben (c) und (d) geht hervor, dass der Lösungsvorschlag 4 zutrifft.