Aufgaben:Aufgabe 4.10Z: Signalraumkonstellation der 16–QAM: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 4.9Z 16–QAM–Signalraumkonstellation nach 4.10Z Signalraumkonstellation der 16–QAM) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1719__Mod_Z_4_9.png|right|]] | + | [[Datei:P_ID1719__Mod_Z_4_9.png|right|frame|Signalraumkonstellation der 16-QAM]] |
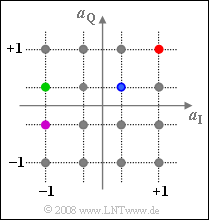
| − | Wir betrachten weiter das 16–QAM–Verfahren entsprechend dem im Theorieteil angegebenen Blockschaltbild. Die Grafik zeigt die möglichen komplexen Amplitudenkoeffizienten $a = | + | Wir betrachten weiter das 16–QAM–Verfahren entsprechend dem im Theorieteil angegebenen Blockschaltbild. Die Grafik zeigt die möglichen komplexen Amplitudenkoeffizienten $a = a_{\rm I} + {\rm j} · a_{\rm Q}$. |
| − | + | ||
| − | + | Für diese Aufgabe soll ebenso wie für die [[Aufgaben:4.10_Signalverläufe_der_16–QAM|Aufgabe 4.10]] vorausgesetzt werden: | |
| − | + | * Die möglichen Amplitudenkoeffizienten $a_{\rm I}$ und $a_{\rm Q}$ der beiden Komponentensignale sind jeweils $ ±1$ und $±1/3$. | |
| + | * Der Sendegrundimpuls $g_s(t)$ ist rechteckförmig und weist die Amplitude $g_0 = 1\ \rm V$ und die Dauer $T = 1 \ \rm μs$ auf. | ||
| + | * Das Quellensignal $q(t)$ vor dem Seriell–Parallel–Wandler ist binär und redundanzfrei. | ||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Quadratur%E2%80%93Amplitudenmodulation|Quadratur–Amplitudenmodulation]]. | ||
| + | *Zur Lösung der Aufgabe ist die Seite [[Modulationsverfahren/Quadratur–Amplitudenmodulation#QAM.E2.80.93Signalraumkonstellationen|QAM–Signalraumkonstellationen]] hilfreich. | ||
| + | *Die zu den farbigen Punkten gehörigen Signale sind auf der Angabenseite zur [[Aufgaben:4.10_Signalverläufe_der_16–QAM|Aufgabe 4.10]] in gleicher Farbe dargestellt. | ||
| + | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| + | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
Version vom 26. Juli 2017, 10:59 Uhr
Wir betrachten weiter das 16–QAM–Verfahren entsprechend dem im Theorieteil angegebenen Blockschaltbild. Die Grafik zeigt die möglichen komplexen Amplitudenkoeffizienten $a = a_{\rm I} + {\rm j} · a_{\rm Q}$.
Für diese Aufgabe soll ebenso wie für die Aufgabe 4.10 vorausgesetzt werden:
- Die möglichen Amplitudenkoeffizienten $a_{\rm I}$ und $a_{\rm Q}$ der beiden Komponentensignale sind jeweils $ ±1$ und $±1/3$.
- Der Sendegrundimpuls $g_s(t)$ ist rechteckförmig und weist die Amplitude $g_0 = 1\ \rm V$ und die Dauer $T = 1 \ \rm μs$ auf.
- Das Quellensignal $q(t)$ vor dem Seriell–Parallel–Wandler ist binär und redundanzfrei.
Hinweise:
- Die Aufgabe gehört zum Kapitel Quadratur–Amplitudenmodulation.
- Zur Lösung der Aufgabe ist die Seite QAM–Signalraumkonstellationen hilfreich.
- Die zu den farbigen Punkten gehörigen Signale sind auf der Angabenseite zur Aufgabe 4.10 in gleicher Farbe dargestellt.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2. Aus der Geometrie folgt für $a = 1 + j$: $$a| = \sqrt{1^2 + 1^2}= \sqrt{2}\hspace{0.15cm}\underline { =1.414}\hspace{0.05cm}, \hspace{0.2cm} {\rm arc}\hspace{0.15cm} a = \arctan \left (\frac {1}{1} \right ) \hspace{0.15cm}\underline {= 45^{\circ}}\hspace{0.05cm}.$$ 3. Der Winkel ergibt sich wie bei der Aufgabe b), der Betrag ist um den Faktor 3 kleiner: |a| = 0.471.
4. Für den komplexen Amplitudenkoeffizienten a = –1 + j/3 erhält man aus der Geometrie: $$|a| = \sqrt{1^2 + (1/3)^2}\hspace{0.15cm}\underline {= 1.054}\hspace{0.05cm},$$ $$ {\rm arc}\hspace{0.15cm} a = 180^{\circ} - \arctan \left (\frac {1}{3} \right ) = 180^{\circ} - 18.43^{\circ} \hspace{0.15cm}\underline {= 161.57^{\circ}}\hspace{0.05cm}.$$ 5. Das violette Symbol hat den gleichen Betrag 1.054 wie das grüne Symbol nach Teilaufgabe c), während der Phasenwinkel das Vorzeichen ändert: arc a = –161.57°.
6. Für den Betrag sind $N_{|a|} = 3$ verschiedene Ergebnisse möglich: 1.414, 1.054 und 0.471. Dagegen gibt es $N_{arc} = 12$ mögliche Phasenlagen: $$ \pm \arctan (1/3) = \pm 18.43^{\circ}, \hspace{0.2cm}\pm \arctan (1) = \pm 45^{\circ}, \hspace{0.2cm}\pm \arctan (3) = \pm 71.57^{\circ}\hspace{0.05cm},$$ $$\pm (180^{\circ}-71.57^{\circ}) = \pm 108.43^{\circ}, \hspace{0.2cm}\pm (180^{\circ}-45^{\circ}) = \pm 135^{\circ}, \hspace{0.2cm}\pm 161.57^{\circ} \hspace{0.05cm}.$$