Aufgaben:Aufgabe 5.3Z: Realisierung einer PN–Sequenz: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1886__Mod_Z_5_3.png|right|]] | + | [[Datei:P_ID1886__Mod_Z_5_3.png|right|frame|Zur Realisierung von PN–Generatoren]] |
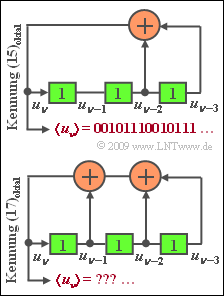
| − | Die Grafik zeigt zwei mögliche Generatoren zur Erzeugung von PN–Sequenzen in unipolarer Darstellung: $u_ν | + | Die Grafik zeigt zwei mögliche Generatoren zur Erzeugung von PN–Sequenzen in unipolarer Darstellung: $u_ν ∈ \{0, 1\}$. |
| − | $$ g_0 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_1 = 0 \hspace{0.05cm}, \hspace{0.2cm}g_2 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_3 = 1 \hspace{0.05cm}.$$ | + | *Der obere Generator mit den Koeffizienten |
| − | wird durch die Oktalkennung $(g_3, g_2, g_1, g_0)_{oktal} = (15)$ bezeichnet. Entsprechend ist die Oktalkennung des zweiten PN–Generators gleich (17). | + | :$$ g_0 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_1 = 0 \hspace{0.05cm}, \hspace{0.2cm}g_2 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_3 = 1 \hspace{0.05cm}.$$ |
| + | wird durch die Oktalkennung $(g_3, g_2, g_1, g_0)_{\rm oktal} = (15)$ bezeichnet. | ||
| + | *Entsprechend ist die Oktalkennung des zweiten PN–Generators gleich (17). | ||
| − | Man spricht von einer M–Sequenz, wenn für die Periodenlänge der Folge | + | |
| + | Man spricht von einer M–Sequenz, wenn für die Periodenlänge der Folge $〈u_ν〉$ gilt: | ||
| + | :$$P = 2^G – 1.$$ | ||
| + | Hierbei bezeichnet $G$ den Grad des Schieberegisters, der gleich der Anzahl der Speicherzellen ist. | ||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Spreizfolgen_für_CDMA|Spreizfolgen für CDMA]]. | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Spreizfolgen_für_CDMA|Spreizfolgen für CDMA]]. | ||
| + | *Bezug genommen wird aber auch auf das Kapitel [[Stochastische_Signaltheorie/Erzeugung_von_diskreten_Zufallsgr%C3%B6%C3%9Fen |Erzeugung von diskreten Zufallsgrößen]] im Buch „Stochastische Signaltheorie”. | ||
| + | * Wir möchten Sie gerne auch auf das Lernvideo [[Erläuterung_der_PN–Generatoren_an_einem_Beispiel_(Lernvideo)|Erläuterung der PN–Generatoren an einem Beispiel]] hinweisen. | ||
*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | *Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist der Grad der PN–Generatoren? | + | {Wie groß ist der Grad $G$ der beiden hier betrachteten PN–Generatoren? |
|type="{}"} | |type="{}"} | ||
| − | $G$ | + | $G \ = \ $ { 3 } |
| − | {Geben Sie die Periodenlänge des PN–Generators | + | {Geben Sie die Periodenlänge $P$ des PN–Generators mit der Oktalkennung (15) an. |
|type="{}"} | |type="{}"} | ||
| − | $P$ | + | $P\ = \ $ { 7 } |
| − | {Welche der | + | {Welche der folgenden Aussagen treffen für jede M–Sequenz zu? |
|type="[]"} | |type="[]"} | ||
- Die Anzahl der Nullen und Einsen ist gleich. | - Die Anzahl der Nullen und Einsen ist gleich. | ||
+ In jeder Periode gibt es eine Eins mehr als Nullen. | + In jeder Periode gibt es eine Eins mehr als Nullen. | ||
| − | + Die maximale Anzahl aufeinander folgender Einsen ist G. | + | + Die maximale Anzahl aufeinander folgender Einsen ist $G$. |
| − | + Die Folge 1 0 1 0 1 0 ... | + | + Die Folge „1 0 1 0 1 0 ... ” ist nicht möglich. |
| − | {Geben Sie die Periodenlänge des | + | {Geben Sie die Periodenlänge $P$ des PN–Generators mit der Oktalkennung (17) an |
|type="{}"} | |type="{}"} | ||
| − | $P$ | + | $P\ = \ $ { 1 } |
{Welcher PN–Generator liefert eine M–Sequenz? | {Welcher PN–Generator liefert eine M–Sequenz? | ||
|type="[]"} | |type="[]"} | ||
| − | + Generator | + | + Der Generator mit der Oktalkennung (15). |
| − | - Generator | + | - Der Generator mit der Oktalkennung (17). |
</quiz> | </quiz> | ||
Version vom 1. August 2017, 17:21 Uhr
Die Grafik zeigt zwei mögliche Generatoren zur Erzeugung von PN–Sequenzen in unipolarer Darstellung: $u_ν ∈ \{0, 1\}$.
- Der obere Generator mit den Koeffizienten
- $$ g_0 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_1 = 0 \hspace{0.05cm}, \hspace{0.2cm}g_2 = 1 \hspace{0.05cm}, \hspace{0.2cm}g_3 = 1 \hspace{0.05cm}.$$
wird durch die Oktalkennung $(g_3, g_2, g_1, g_0)_{\rm oktal} = (15)$ bezeichnet.
- Entsprechend ist die Oktalkennung des zweiten PN–Generators gleich (17).
Man spricht von einer M–Sequenz, wenn für die Periodenlänge der Folge $〈u_ν〉$ gilt:
- $$P = 2^G – 1.$$
Hierbei bezeichnet $G$ den Grad des Schieberegisters, der gleich der Anzahl der Speicherzellen ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Spreizfolgen für CDMA.
- Bezug genommen wird aber auch auf das Kapitel Erzeugung von diskreten Zufallsgrößen im Buch „Stochastische Signaltheorie”.
- Wir möchten Sie gerne auch auf das Lernvideo Erläuterung der PN–Generatoren an einem Beispiel hinweisen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2. Aus der angegebenen Folge ist die Periodenlänge P = 7 ablesbar. Wegen $P = 2^G –1$ handelt es sich um eine M–Sequenz.
3. Die maximale Anzahl aufeinander folgender Einsen ist G (nämlich immer dann, wenn in allen G Speicherzellen eine Eins steht). Es ist dagegen nicht möglich, dass alle Speicherzellen mit Nullen belegt sind (da sonst nur noch Nullen erzeugt würden). Deshalb gibt es stets eine Eins mehr als Nullen.
Die Periodenlänge der letzten Folge beträgt P = 2. Bei einer M–Sequenz gilt dagegen $P = 2^G –1$. Für keinen Wert von G ist P = 2 möglich.
Richtig sind somit die Lösungsvorschläge 2, 3 und 4.
4. Sind alle Speicherzellen mit Einsen belegt, so liefert der Generator $(17)_{okta}$ wieder eine 1: $$u_{\nu} \left [ u_{\nu-1} + u_{\nu-2} + u_{\nu-3} \right ] \,\,{\rm mod} \,\,2 =1 \hspace{0.05cm}.$$ Da sich so an der Speicherbelegung nichts ändert, werden auch alle weiteren erzeugten Binärwerte jeweils 1 sein ⇒ P = 1.
5. Richtig ist Antwort 1: Von einer M–Sequenz spricht man nur dann, wenn $P = 2^G –1$ gilt. M steht hierbei für „maximal”.