Aufgaben:Aufgabe 5.6Z: Einträger–und Mehrträgersystem

• Zurück zum Buch

In dieser Aufgabe soll ein Vergleich zwischen

• einem Einträgersystem ($N = 1$) und
• einem Mehrträgersystem mit $N = 32$ Trägern erfolgen. Für beide Übertragungssysteme wird jeweils eine Datenbitrate von $R_{\rm B} = 1 \ \rm Mbit/s$ gefordert.

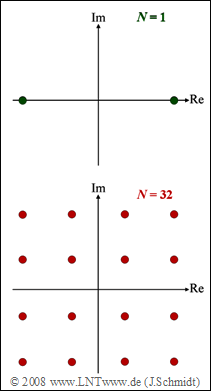
Die Grafik zeigt die verwendeten Signalraumzuordnungen für den Fall von Single–Carrier (SC) bzw. Multi–Carrier (MC).

Hinweise:

• Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung von OFDM.
• Bezug genommen wird auch auf das Kapitel Quadratur-Amplitudenmodulation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welches Mapping verwendet das Einträgersystem?

	ASK,
	BPSK,
	4-QAM
	16-QAM

2

Welches Mapping verwendet das Mehrträgersystem?

	ASK,
	BPSK,
	4-QAM,
	16-QAM

3

Berechnen Sie die Symboldauer $T_{\rm SC}$ des Einträgersystems.

$T_{\rm SC} \ = \ $ $\ \rm μs$

4

Berechnen Sie die Symboldauer $T_{\rm MC}$ des Mehrträgersystems.

$T_{\rm SC} \ = \ $ $\ \rm μs$

5

Welche der folgenden Aussagen treffen zu?

	Die Impulsinterferenzen sind unabhängig von der Symboldauer $T$.
	Die Impulsinterferenzen nehmen mit steigender Symboldauer $T$ ab.
	Die Impulsinterferenzen nehmen mit steigender Symboldauer $T$zu.

Musterlösung

Musterlösung

Musterlösung

(1)  Aus der Grafik auf der Angabenseite erkennt man sofort, dass das Einträgersystem auf binärer Phasenmodulation (BPSK) basiert   ⇒   Lösungsvorschlag 2.

(2)  Dagegen basiert das Mehrträgersystem auf 16–QAM   ⇒   Lösungsvorschlag 3.

(3)  Allgemein gilt bei einem OFDM–System mit $N$ Trägern und $M$ Signalraumpunkten für die Symboldauer:

$$T = N \cdot {\rm{log}_2}\hspace{0.04cm}(M) \cdot T_{\rm{B}}.$$

Wegen $R_{\rm{B}} = 1 \ \rm Mbit/s$ ist die Bitdauer bei der BPSK gleich $T_{\rm{B}} = 1 \ \rm μs$. Daraus ergibt sich für die Symboldauer des Einträgersystems mit $N = 1$ und $M = 2$:

$$ T_{\rm{SC}} = 1 \cdot {\rm{log}_2}\hspace{0.04cm}(2) \cdot T_{\rm{B}}\hspace{0.15cm}\underline {= 1\,\,{\rm \mu s}}.$$

(4)  In gleicher Weise erhält man für das Mehrträgersystem mit $N = 32$ und $M = 16$:

$$T_{\rm{MC}} = 32 \cdot {\rm{log}_2}\hspace{0.04cm}(16) \cdot T_{\rm{B}}\hspace{0.15cm}\underline {= 128\,\,{\rm \mu s}}.$$

(5)  Bei großer Symboldauer ist der relative Anteil, der vom Vorgängersymbol ins betrachtete Symbol hineinreicht und damit Impulsinterferenzen (ISI) bewirkt, kleiner als bei kleiner Symboldauer. Richtig ist demzufolge der Lösungsvorschlag 2.