Aufgaben:Aufgabe 1.2: Lognormal – Kanalmodell: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 6: | Zeile 6: | ||
:$$V_{\rm P} = V_{\rm 0} + V_{\rm S} \hspace{0.05cm}.$$ | :$$V_{\rm P} = V_{\rm 0} + V_{\rm S} \hspace{0.05cm}.$$ | ||
| − | $V_0$ berücksichtigt den entfernungsabhängigen Pfadverlust, der mit $V_0 = 80 \ dB$ als konstant angenommen wird. Der Verlust $ | + | $V_0$ berücksichtigt den entfernungsabhängigen Pfadverlust, der mit $V_0 = 80 \ \rm dB$ als konstant angenommen wird. Der Verlust $V_{\rm S}$ ist auf Abschattungen (<i>Shadowing</i>) zurückzuführen, der durch die Lognormal–Verteilung mit der Wahrscheinlichkeitsdichtefunktion |
:$$f_{V{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ (V_{\rm S}- m_{\rm S})^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}$$ | :$$f_{V{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ (V_{\rm S}- m_{\rm S})^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}$$ | ||
| Zeile 13: | Zeile 13: | ||
Gehen Sie außerdem von folgenden einfachen Annahmen aus: | Gehen Sie außerdem von folgenden einfachen Annahmen aus: | ||
| − | * Die Sendeleistung beträgt $ | + | * Die Sendeleistung beträgt $P_{\rm S} = 10 \ \rm W$ (oder $40 \ \rm dBm$). |
| − | * Die Empfangsleistung soll mindestens $ | + | * Die Empfangsleistung soll mindestens $P_{\rm E} = 10 \ \rm pW$ (umgerechnet: $–80 \ \rm dBm$) betragen. |
| − | + | ''Hinweis:'' | |
| − | Für das komplementäre Gaußsche Fehlerintegral können Sie folgende (grobe) Näherungen verwenden: | + | * Die Aufgabe gehört zum Kapitel [[Mobile_Kommunikation/Distanzabh%C3%A4ngige_D%C3%A4mpfung_und_Abschattung|Distanzabhängige Dämpfung und Abschattung]] dieses Buches. |
| + | * Für das komplementäre Gaußsche Fehlerintegral können Sie folgende (grobe) Näherungen verwenden: | ||
:$${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm} | :$${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm} | ||
{\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$ | {\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$ | ||
| − | + | * Oder Sie benutzen das von LNTwww bereitgestellte [http://www.lntwww.de/cgi-bin/extern/swf-sitemap.pl?swf_id=280&swf=QFunction.swf&swf_hoehe=500&swf_breite=620|'''Flash–Modul''']. | |
| − | Oder Sie benutzen das von LNTwww bereitgestellte [http://www.lntwww.de/cgi-bin/extern/swf-sitemap.pl?swf_id=280&swf=QFunction.swf&swf_hoehe=500&swf_breite=620|'''Flash–Modul''']. | ||
Version vom 27. Oktober 2017, 10:40 Uhr
Wir betrachten eine Mobilfunkzelle im städtischen Bereich und ein Fahrzeug, das sich näherungsweise in einem festen Abstand $d_0$ von der Basisstation aufhält. Beispielsweise bewegt es sich auf einem Kreisbogen um die Basisstation. Somit ist der gesamte Pfadverlust durch folgende Gleichung beschreibbar:
- $$V_{\rm P} = V_{\rm 0} + V_{\rm S} \hspace{0.05cm}.$$
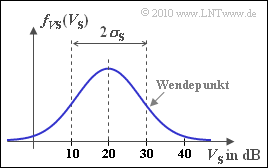
$V_0$ berücksichtigt den entfernungsabhängigen Pfadverlust, der mit $V_0 = 80 \ \rm dB$ als konstant angenommen wird. Der Verlust $V_{\rm S}$ ist auf Abschattungen (Shadowing) zurückzuführen, der durch die Lognormal–Verteilung mit der Wahrscheinlichkeitsdichtefunktion
- $$f_{V{\rm S}}(V_{\rm S}) = \frac {1}{ \sqrt{2 \pi }\cdot \sigma_{\rm S}} \cdot {\rm exp } \left [ - \frac{ (V_{\rm S}- m_{\rm S})^2}{2 \cdot \sigma_{\rm S}^2} \right ] \hspace{0.05cm}$$
ausreichend genau beschrieben wird (siehe Grafik). Es gelten folgende Zahlenwerte:
- $$m_{\rm S} = 20\,\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm} \sigma_{\rm S} = 10\,\,{\rm dB}\hspace{0.15cm}{\rm bzw.}\hspace{0.15cm}\sigma_{\rm S} = 0\,\,{\rm dB}\hspace{0.15cm}{\rm (Teilaufgabe\hspace{0.15cm} b)}\hspace{0.05cm}.$$
Gehen Sie außerdem von folgenden einfachen Annahmen aus:
- Die Sendeleistung beträgt $P_{\rm S} = 10 \ \rm W$ (oder $40 \ \rm dBm$).
- Die Empfangsleistung soll mindestens $P_{\rm E} = 10 \ \rm pW$ (umgerechnet: $–80 \ \rm dBm$) betragen.
Hinweis:
- Die Aufgabe gehört zum Kapitel Distanzabhängige Dämpfung und Abschattung dieses Buches.
- Für das komplementäre Gaußsche Fehlerintegral können Sie folgende (grobe) Näherungen verwenden:
- $${\rm Q}(1) \approx 0.16\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(2) \approx 0.02\hspace{0.05cm},\hspace{0.2cm} {\rm Q}(3) \approx 10^{-3}\hspace{0.05cm}.$$
- Oder Sie benutzen das von LNTwww bereitgestellte Flash–Modul.
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.