Aufgaben:Aufgabe 1.08Z: BPSK-Fehlerwahrscheinlichkeit: Unterschied zwischen den Versionen
Aus LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Digitalsignalübertragung/Lineare digitale Modulation – Kohärente Demodulation }} [[Datei:|right|]] ===Fragebogen=== <quiz disp…“) |
|||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
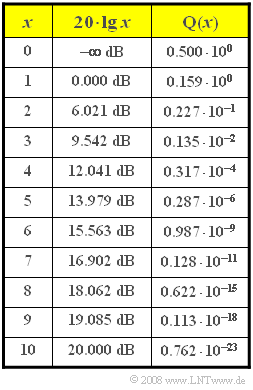
| − | [[Datei:|right|]] | + | [[Datei:P_ID1681__Dig_Z_4_1.png|right|frame|Komplementäre Gaußsche Fehlerfunktion]] |
| + | Wir gehen von dem optimalen Basisbandübertragungssystem für Binärsignale aus mit | ||
| + | *bipolaren Amplitudenkoeffizienten $a_{\nu} \in$ {$–1$, $+1$}, | ||
| + | *rechteckförmigem Sendesignal mit den Signalwerten $\pm s_{0}$ und der Bitdauer $T_{\rm B}$, | ||
| + | *AWGN–Rauschen mit der Rauschleistungsdichte $N_{0},$ | ||
| + | *Empfangsfilter gemäß dem Matched–Filter–Prinzip, | ||
| + | *Entscheider mit der optimalen Schwelle $E = 0$. | ||
| + | |||
| + | |||
| + | Wenn nichts anderes angegeben ist, so sollten Sie zudem von den folgenden Zahlenwerten ausgehen: | ||
| + | :$$ s_0 = 4\,{\rm V},\hspace{0.2cm} T_{\rm B} = 1\,{\rm ns},\hspace{0.2cm}N_0 = 2 \cdot 10^{-9}\, {\rm V^2/Hz} \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Bitfehlerwahrscheinlichkeit dieses „Basisbandsystems” wurde bereits in [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung|Fehlerwahrscheinlichkeit bei Basisbandübertragung]] angegeben (Index BB): | ||
| + | :$$p_{\rm BB} = {\rm Q}\left ( \frac{s_0}{{\sigma_d }} \right )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\sigma_d = \sqrt{\frac{N_0}{2 \cdot T_{\rm B}}}.$$ | ||
| + | |||
| + | Hierbei bezeichnet $\sigma_{d}$ den Rauscheffektivwert am Entscheider und Q$(x)$ die komplementäre Gaußsche Fehlerfunktion, die hier tabellarisch gegeben ist. | ||
| + | Diese Fehlerwahrscheinlichkeit kann man auch in der Form | ||
| + | :$$p_{\rm BB} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right )$$ | ||
| + | schreiben, wobei $E_{\rm B}$ die „Energie pro Bit” bezeichnet. Die Fehlerwahrscheinlichkeit eines vergleichbaren Übertragungssystems mit Binary Phase Shift Keying (BPSK) lautet: | ||
| + | :$$p_{\rm BPSK} = {\rm Q}\left ( {s_0}/{{\sigma_d }} \right )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/{T_{\rm B}}}.$$ | ||
| + | |||
| + | |||
Version vom 6. November 2017, 20:55 Uhr
Wir gehen von dem optimalen Basisbandübertragungssystem für Binärsignale aus mit
- bipolaren Amplitudenkoeffizienten $a_{\nu} \in$ {$–1$, $+1$}, *rechteckförmigem Sendesignal mit den Signalwerten $\pm s_{0}$ und der Bitdauer $T_{\rm B}$, *AWGN–Rauschen mit der Rauschleistungsdichte $N_{0},$ *Empfangsfilter gemäß dem Matched–Filter–Prinzip, *Entscheider mit der optimalen Schwelle $E = 0$. Wenn nichts anderes angegeben ist, so sollten Sie zudem von den folgenden Zahlenwerten ausgehen: :'"`UNIQ-MathJax2-QINU`"' Die Bitfehlerwahrscheinlichkeit dieses „Basisbandsystems” wurde bereits in [[Digitalsignalübertragung/Fehlerwahrscheinlichkeit_bei_Basisbandübertragung|Fehlerwahrscheinlichkeit bei Basisbandübertragung]] angegeben (Index BB): :'"`UNIQ-MathJax3-QINU`"' Hierbei bezeichnet $\sigma_{d}$ den Rauscheffektivwert am Entscheider und Q$(x)$ die komplementäre Gaußsche Fehlerfunktion, die hier tabellarisch gegeben ist. Diese Fehlerwahrscheinlichkeit kann man auch in der Form :'"`UNIQ-MathJax4-QINU`"' schreiben, wobei $E_{\rm B}$ die „Energie pro Bit” bezeichnet. Die Fehlerwahrscheinlichkeit eines vergleichbaren Übertragungssystems mit Binary Phase Shift Keying (BPSK) lautet:
- $$p_{\rm BPSK} = {\rm Q}\left ( {s_0}/[[:Vorlage:\sigma d]] \right )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}\sigma_d = \sqrt{{N_0}/{T_{\rm B}}}.$$
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
(6)