Aufgaben:Aufgabe 1.3: Rechteckfunktionen für Sender und Empfänger

• Zurück zum Buch

Vergleich dreier verschiedener Systemkonzepte

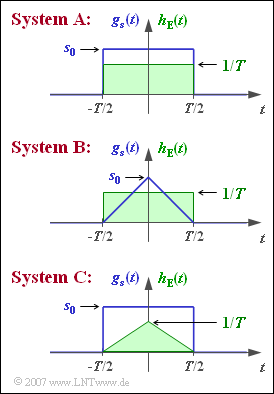
Wir betrachten hier drei Varianten eines binären bipolaren AWGN–Übertragungssystems, die sich hinsichtlich des Sendegrundimpulses $g_{\rm s}(t)$ sowie der Impulsantwort $h_{\rm E}(t)$ des Empfangsfilters unterscheiden:

• Beim System A sind beide Zeitfunktionen $g_{\rm s}(t)$ und $h_{\rm E}(t)$ rechteckförmig, lediglich die Impulshöhen ($s_{\rm 0}$ bzw. $1/T$) sind unterschiedlich.
• Das System B unterscheidet sich vom System A durch einen dreieckförmigen Sendegrundimpuls mit $g_{\rm s}(t=0) = s_{\rm 0}$.
• Das System C hat den gleichen Sendegrundimpuls wie das System A, während die Impulsantwort mit $h_{\rm E}(t=0) = 1/T$ dreieckförmig verläuft.

Die absolute Breite der hier betrachteten Rechteck– und Dreieckfunktionen beträgt jeweils $T = 10 \ \rm \mu s$. Die Bitrate ist $R = 100 \ \rm kbit/s$. Die weiteren Systemparameter sind wie folgt gegeben:

$$s_0 = 6 \,\,\sqrt{W}\hspace{0.05cm},\hspace{0.3cm} N_{\rm 0} = 2 \cdot 10^{-5} \,\,{\rm W/Hz}\hspace{0.05cm}.$$

Hinweise:

Die Aufgabe bezieht sich auf das Fehlerwahrscheinlichkeit bei Basisbandübertragung des vorliegenden Buches. Zur Bestimmung von Fehlerwahrscheinlichkeiten können Sie das folgende Interaktionsmodul verwenden:

Komplementäre Gaußsche Fehlerfunktionen

Berücksichtigen Sie bei der Berechnung der Detektionsstörleistung das Theorem von Wiener–Chintchine:

$$ \sigma _d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H_{\rm E}( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {h_{\rm E}( t )} \right|^2 \hspace{0.1cm}{\rm{d}}t}\hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie den Detektionsgrundimpuls $g_{\rm d}(t) = g_{\rm s}(t) ∗ h_{\rm E}(t)$ für System A. Welcher Wert ergibt sich für den Zeitpunkt $t = 0$?

$System\ A: g_{\rm d}(t = 0) \ = \ $ $\ \rm W^{1/2}$

2

Berechnen Sie die Detektionsstörleistung für das System A.

$System\ A: σ_{\rm d}\ ^2 \ = \ $ $\ \rm W$

3

Welche Bitfehlerwahrscheinlichkeit ergibt sich für das System A?

$System\ A: p_{\rm B} \ = \ $ $\ \cdot 10^{-9}$

4

Ermitteln Sie die entsprechenden Größen für das System B.

$System\ B: g_{\rm d}(t = 0) \ = \ $ $\ \rm W^{1/2}$

Musterlösung

Musterlösung

1. 2. 3. 4. 5. 6. 7.