Aufgaben:Aufgabe 2.2: Binäre bipolare Rechtecke

• Zurück zum Buch

Beispiele für binäre bipolare Rechtecksignale

Wir gehen von folgendem Signal aus:

$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$

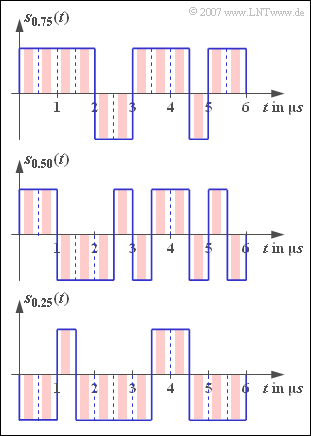
Der Sendegrundimpuls $g_{s}(t)$ wird in dieser Aufgabe stets als rechteckförmig angenommen, wobei das NRZ–Format (blaue Signalverläufe in der Grafik) als auch das RZ–Format mit dem Tastverhältnis $T_{\rm S}/T = 0.5$ (rote Signalverläufe) zu untersuchen ist.

Die Amplitudenkoeffizienten besitzen die folgenden Eigenschaften:

• Sie sind binär und bipolar: $a_{\nu} ∈ \{–1, +1\}$.
• $\langle a_{\nu }\rangle$ weist keine statistischen Bindungen auf.
• Die Wahrscheinlichkeiten für die beiden möglichen Werte $±1$ lauten mit $0 < p < 1$:

$${\rm Pr}(a_\nu = +1) \ = \ p,$$

$${\rm Pr}(a_\nu = -1) \ = \ 1 - p \hspace{0.05cm}.$$

Die drei in der Grafik dargestellten Signalausschnitte gelten für $p = 0.75$, $p = 0.50$ und $p = 0.25$.

Im Laufe dieser Aufgabe wird auf folgende Beschreibungsgrößen Bezug genommen:

• $m_{a} = \E[a_{\nu}]$ gibt den linearen Mittelwert der Amplitudenkoeffizienten an, und $m_{2a} = \E[a_{\nu}^{2}]$ ist der quadratische Mittelwert. Damit kann auch die Varianz $\sigma_{a}^{2} = m_{2a} – m_{a}^{2}$ berechnet werden.
• Die diskrete AKF der Amplitudenkoeffizienten ist $\varphi_{a}(\lambda) = \E[a_{\nu} \cdot a_{\nu} + \lambda]$. Es gilt hier:

$$\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 \\ m_1^2 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \hspace{0.05cm}.\\ \end{array}$$

• Die Energie–AKF des Sendegrundimpulses beträgt:

$$\varphi^{^{\bullet}}_{gs}(\tau) = \left\{ \begin{array}{c} s_0^2 \cdot T_{\rm S} \cdot \left( 1 - {|\tau|}/{T_{\rm S}}\right) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}|\tau| \le T_{\rm S} \\ |\tau| \ge T_{\rm S} \hspace{0.05cm}.\\ \end{array}$$

• Damit erhält man für die gesamte AKF des Sendesignals:

$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$

• Das Leistungsdichtespektrum $\Phi_{s}(f)$ ist die Fouriertransformierte der AKF $\varphi_{s}(\tau)$.

Hinweis:

Diese Aufgabe bezieht sich auf Grundlagen der codierten Übertragung des Buches „Digitalsignalübertragung”.

Fragebogen

1

Welche der drei dargestellten Signale sind redundanzfrei?

	$s_{0.75}(t)$,
	$s_{0.50}(t)$,
	$s_{0.25}(t)$,

2

Wie groß ist der quadratische Mittelwert $m_{2a}$ der Amplitudenkoeffizienten in Abhängigkeit von $p$?

$p = 0.75 : m_{2a} \ = \ $

$p = 0.50 : m_{2a} \ = \ $

$p = 0.25 : m_{2a} \ = \ $

3

Berechnen Sie den linearen Mittelwert $m_{a}$ in Abhängigkeit von $p$.

$p = 0.75 : m_{a} \ = \ $

$p = 0.50 : m_{a} \ = \ $

$p = 0.25 : m_{a} \ = \ $

4

Wie groß ist die Varianz $\sigma_{a}^{2}$ der Amplitudenkoeffizienten?

$p = 0.75 : \sigma_{a}^{2} \ = \ $

$p = 0.50 : \sigma_{a}^{2} \ = \ $

$p = 0.25 : \sigma_{a}^{2} \ = \ $

5

Es gelte zunächst $p = 0.5$. Skizzieren Sie die AKF $\varphi_{s}(\tau)$ für den NRZ– und den RZ–Grundimpuls und bewerten Sie folgende Aussagen:

	Die AKF ist in beiden Fällen dreieckförmig.
	Das LDS verläuft in beiden Fällen ${\rm si}^{2}$–förmig.
	Die LDS–Fläche ist in beiden Fällen gleich.
	Bei RZ–Impulsen beinhaltet $\Phi_{s}(f)$ zusätzliche Diracfunktionen.

6

Es gelte nun $p = 0.75$. Skizzieren Sie die AKF für den NRZ–Grundimpuls und bewerten Sie folgende Aussagen:

	Die AKF besteht aus einem Dreieck und einem Gleichanteil.
	Das LDS besteht aus einem ${\rm si}^{2}$–Anteil und einem Dirac.
	Die Diracfunktion hat das Gewicht $s_{0}^{2}$.
	Mit $p = 0.25$ ergibt sich das gleiche Leistungsdichtespektrum.

7

Es gelte weiter $p = 0.75$. Skizzieren Sie die AKF für den RZ–Grundimpuls und bewerten Sie folgende

	Auch hier beinhaltet das LDS einen ${\rm si}^{2}$–förmigen Anteil.
	Gleichzeitig gibt es im LDS noch unendlich viele Diraclinien.

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)  (6)