Aufgaben:Aufgabe 2.6: Einheiten bei GWSSUS: Unterschied zwischen den Versionen
Aus LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Mobile Kommunikation/Das GWSSUS–Kanalmodell}} right|frame|Mobilfunk–Szenario mit 3 Pfaden…“) |
|||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Das GWSSUS–Kanalmodell}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Das GWSSUS–Kanalmodell}} | ||
| − | [[Datei: | + | [[Datei:P_ID2167__Mob_A_2_6.png|right|frame|GWSSUS–Funktionen]] |
| + | Der Mobilfunkkanal kann in sehr allgemeinen Form durch vier Systemfunktionen beschrieben werden, wobei der Zusammenhang zwischen je zwei Funktionen durch | ||
| + | * die Fouriertransformation bzw. | ||
| + | * die Fourierrücktransformation | ||
| + | |||
| + | |||
| + | gegeben ist. | ||
| + | |||
| + | Wir bezeichnen die Funktionen einheitlich mit $\eta_{12}$. Die Indizes seien wie folgt vereinbart: | ||
| + | * <b>V</b> steht für Verzögerung $\tau$ (Index „$1$”), | ||
| + | * <b>F</b> steht für die Frequenz $f$ (Index „$1$”), | ||
| + | * <b>Z</b> steht für die Zeit $t$ (Index „$2$”), | ||
| + | * <b>D</b> ist die Dopplerfrequenz $f$ (Index „$2$”). | ||
| + | |||
| + | |||
| + | Der Zusammenhang zwischen den Funktionen ist in der oberen Grafik (gelbe Hinterlegung) dargestellt. Fourierkorrespondenzen sind grün eingezeichnet: | ||
| + | * Der Übergang von einem weiß gefüllten zu einem grün gefüllten Kreis entspricht einer [[Fouriertransformation]]. | ||
| + | * Der Übergang von einem grün gefüllten zu einem weiß gefüllten Kreis (Gegenrichtung) entspricht einer [[Fourierrücktransformation]]. | ||
| + | |||
| + | |||
| + | Beispielsweise gilt: | ||
| + | |||
Version vom 20. November 2017, 09:42 Uhr
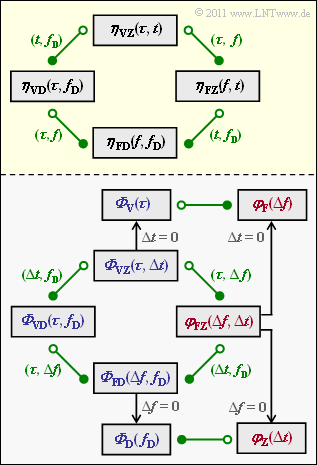
Der Mobilfunkkanal kann in sehr allgemeinen Form durch vier Systemfunktionen beschrieben werden, wobei der Zusammenhang zwischen je zwei Funktionen durch
- die Fouriertransformation bzw.
- die Fourierrücktransformation
gegeben ist.
Wir bezeichnen die Funktionen einheitlich mit $\eta_{12}$. Die Indizes seien wie folgt vereinbart:
- V steht für Verzögerung $\tau$ (Index „$1$”),
- F steht für die Frequenz $f$ (Index „$1$”),
- Z steht für die Zeit $t$ (Index „$2$”),
- D ist die Dopplerfrequenz $f$ (Index „$2$”).
Der Zusammenhang zwischen den Funktionen ist in der oberen Grafik (gelbe Hinterlegung) dargestellt. Fourierkorrespondenzen sind grün eingezeichnet:
- Der Übergang von einem weiß gefüllten zu einem grün gefüllten Kreis entspricht einer Fouriertransformation.
- Der Übergang von einem grün gefüllten zu einem weiß gefüllten Kreis (Gegenrichtung) entspricht einer Fourierrücktransformation.
Beispielsweise gilt:
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)