Aufgaben:Aufgabe 2.6: Einheiten bei GWSSUS: Unterschied zwischen den Versionen
| Zeile 23: | Zeile 23: | ||
Beispielsweise gilt: | Beispielsweise gilt: | ||
| + | :$$\eta_{\rm VZ}(\tau, t) | ||
| + | \hspace{0.2cm} \stackrel{\tau, \hspace{0.02cm}f}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \eta_{\rm FZ}(f,t)\hspace{0.05cm}, | ||
| + | \hspace{0.4cm}\eta_{\rm FZ}(f,t) | ||
| + | \hspace{0.2cm} \stackrel{f, \hspace{0.02cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.05cm}.$$ | ||
| + | Die hieraus abgeleitete Korrelationsfunktion „$\varphi_{12}$” und das Leistungsdichtespektrum „$\it \Phi_{12}$” werden mit den gleichen Indizes versehen wie die Systemfunktion $\eta_{12}$. Korrealtionsfunktionen erkennt man in der unteren Grafik an der roten Schrift und alle Leistungsdichtespektren sind blau beschriftet. Es wird stets vom GWSSUS–Modell ausgegangen. | ||
| + | |||
| + | Betrachten wir hier die Systemfunktion $\eta_{\rm VZ}(\tau, t)$, also die zeitvariante Impulsantwort $h(\tau, t)$. Für diese ergeben sich folgende Beschreibungsgrößen: | ||
| + | :$$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot | ||
| + | \eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm},$$ | ||
| + | :$$\Delta \tau = \tau_2 - \tau_1 \hspace{0.05cm}, \hspace{0.2cm} \Delta t = t_2 - t_1 | ||
| + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| + | \varphi_{\rm VZ}(\Delta \tau, \Delta t) \hspace{0.05cm}, $$ | ||
| + | :$$\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.$$ | ||
| + | :$${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau, \Delta t = 0)\hspace{0.05cm}. $$ | ||
| + | |||
| + | ''Hinweis:'' | ||
| + | * Die Aufgabe gehört zum Kapitel [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell| Das GWSUS–Kanalmodell]]. | ||
Version vom 20. November 2017, 11:32 Uhr
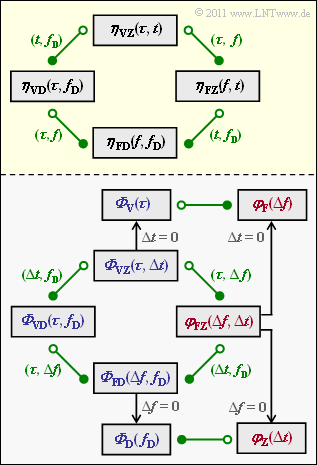
Der Mobilfunkkanal kann in sehr allgemeinen Form durch vier Systemfunktionen beschrieben werden, wobei der Zusammenhang zwischen je zwei Funktionen durch
- die Fouriertransformation bzw.
- die Fourierrücktransformation
gegeben ist.
Wir bezeichnen die Funktionen einheitlich mit $\eta_{12}$. Die Indizes seien wie folgt vereinbart:
- V steht für Verzögerung $\tau$ (Index „$1$”),
- F steht für die Frequenz $f$ (Index „$1$”),
- Z steht für die Zeit $t$ (Index „$2$”),
- D ist die Dopplerfrequenz $f$ (Index „$2$”).
Der Zusammenhang zwischen den Funktionen ist in der oberen Grafik (gelbe Hinterlegung) dargestellt. Fourierkorrespondenzen sind grün eingezeichnet:
- Der Übergang von einem weiß gefüllten zu einem grün gefüllten Kreis entspricht einer Fouriertransformation.
- Der Übergang von einem grün gefüllten zu einem weiß gefüllten Kreis (Gegenrichtung) entspricht einer Fourierrücktransformation.
Beispielsweise gilt:
- $$\eta_{\rm VZ}(\tau, t) \hspace{0.2cm} \stackrel{\tau, \hspace{0.02cm}f}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \eta_{\rm FZ}(f,t)\hspace{0.05cm}, \hspace{0.4cm}\eta_{\rm FZ}(f,t) \hspace{0.2cm} \stackrel{f, \hspace{0.02cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.05cm}.$$
Die hieraus abgeleitete Korrelationsfunktion „$\varphi_{12}$” und das Leistungsdichtespektrum „$\it \Phi_{12}$” werden mit den gleichen Indizes versehen wie die Systemfunktion $\eta_{12}$. Korrealtionsfunktionen erkennt man in der unteren Grafik an der roten Schrift und alle Leistungsdichtespektren sind blau beschriftet. Es wird stets vom GWSSUS–Modell ausgegangen.
Betrachten wir hier die Systemfunktion $\eta_{\rm VZ}(\tau, t)$, also die zeitvariante Impulsantwort $h(\tau, t)$. Für diese ergeben sich folgende Beschreibungsgrößen:
- $$\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1, t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2, t_2) \right ]\hspace{0.05cm},$$
- $$\Delta \tau = \tau_2 - \tau_1 \hspace{0.05cm}, \hspace{0.2cm} \Delta t = t_2 - t_1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_{\rm VZ}(\Delta \tau, \Delta t) \hspace{0.05cm}, $$
- $$\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.$$
- $${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau, \Delta t = 0)\hspace{0.05cm}. $$
Hinweis:
- Die Aufgabe gehört zum Kapitel Das GWSUS–Kanalmodell.
Fragebogen
Musterlösung