Aufgaben:Aufgabe 1.1: Zur Kennzeichnung aller Bücher

• Zurück zum Buch

ISBN–10? Oder ISBN–13?

Seit den 1960er Jahren werden alle Bücher mit einer 10–stelligen International Standard Book Number versehen. Die letzte Ziffer dieser sog. ISBN–10–Angabe berechnet sich dabei entsprechend folgender Regel:

$$ z_{10}= \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.2cm} \mod 11 \hspace{0.05cm}.$$

Seit 2007 ist zusätzlich die Angabe entsprechend des Standards ISBN–13 verpflichtend, wobei die Prüfziffer $z_{\rm 13}$ sich dann wie folgt ergibt:

$$z_{13} = 10 - \left ( \sum_{i=1}^{12} \hspace{0.2cm} z_i \cdot 3^{(i+1)\mod 2} \right ) \hspace{-0.2cm} \mod 10 \hspace{0.05cm}.$$

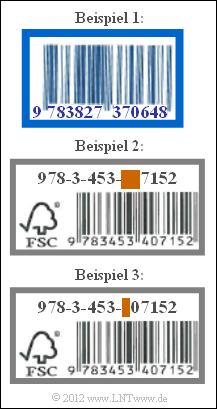
Nebenstehend sind einige beispielhafte ISBN angegeben. Hierauf beziehen sich die folgenden Fragen.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel Zielsetzung_der_Kanalcodierung

Fragebogen

1

Um welchen Standard handelt es sich bei Beispiel 1?

	ISBN–10,
	ISBN–13.

2

Entsprechend Beispiel 2 sind zwei Ziffern einer ISBN–13 ausgelöscht. Kann man die ISBN rekonstruieren? Wenn Ja: Geben Sie die ISBN–13 an.

	ja,
	Nein.

3

Entsprechend Beispiel 3 ist eine Ziffer einer ISBN–13 ausgelöscht. Kann die ISBN rekonstruiert werden? Wenn Ja: Geben Sie die ISBN–13 an.

	Ja,
	Nein.

4

Wieviele verschiedene Werte kann die Prüfziffer $z_{\rm 10}$ bei ISBN–10 annehmen?

$M \ = \ $ $\ \rm$

5

Mitgeteilt als ISBN–10 wird 3–8273–7064–7. Welche Aussage trifft zu?

	Dies ist keine zulässige ISBN.
	Die ISBN könnte richtig sein.
	Die ISBN ist mit Sicherheit richtig.

Musterlösung

Musterlösung

(1)  Allein durch Abzählen der ISBN–Ziffern erkennt man, dass Antwort 2 richtig ist. Die gewichtete Summe über alle Ziffern ergibt ein Vielfaches von 10:

$$S \ = \ \hspace{-0.1cm} \sum_{i=1}^{13} \hspace{0.2cm} z_i \cdot 3^{(i+1) \hspace{-0.2cm} \mod 2} =$$

$$ \ = \ \hspace{-0.1cm} (9+8+8+7+7+6+8) \cdot 1 + (7+3+2+3+0+4) \cdot 3 = 110$$

$$\Rightarrow \hspace{0.3cm} S \hspace{-0.2cm} \mod 10 \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$

(2)  Die Antwort ist Nein. Mit einer einzigen Prüfziffer lässt sich nur eine Auslöschung rekonstruieren.

(3)  Eine Ziffer kann rekonstruiert werden ⇒ Ja. Für die Ziffer $z_{\rm 8}$ muss gelten:

$$[(9+8+4+3+0+1+2) \cdot 1 + (7+3+5+z_8+7+5) \cdot 3] \hspace{-0.2cm} \mod 10 = 0$$

$$\Rightarrow \hspace{0.3cm} [108 + 3z_8] \hspace{-0.2cm} \mod 10 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_8 \hspace{0.15cm}\underline {= 4} \hspace{0.05cm}.$$

(4)  Durch die Modulo–11–Operation kann z10 die Werte 0, 1, ... , 10 annehmen ⇒ M =11. Da „10” keine Ziffer ist, behilft man sich mit z10 = „X”. Dies entspricht der römischen Darstellung der Zahl „10”.

(5)  Die Prüfbedingung lautet:

$$S= \left ( \sum_{i=1}^{10} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.2cm} \mod 11 = 0 \hspace{0.05cm}.$$

Die gegebene ISBN erfüllt diese Bedingung:

Richtig ist die Aussage 2, da sich die Prüfsumme S = 0 auch bei mehr als einem Fehler ergeben könnte.