Aufgaben:Aufgabe 2.5: Ternäre Signalübertragung

• Zurück zum Buch

WDF eines verrauschten Ternärsignals

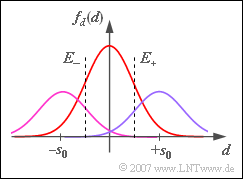
Betrachtet wird ein ternäres Übertragungssystem ($M = 3$) mit den möglichen Amplitudenwerten $–s_0$, $0$ und $+s_0$. Bei der Übertragung addiert sich dem Signal ein additives Gaußsches Rauschen mit dem Effektivwert $\sigma_d$. Die Rückgewinnung des dreistufigen Digitalsignals beim Empfängers geschieht mit Hilfe von zwei Entscheiderschwellen bei $E_{–}$ bzw. $E_{+}$.

Zunächst werden die Auftrittswahrscheinlichkeiten von den drei Eingangssymbolen als gleichwahrscheinlich angenommen

$$p_{\rm -} = {\rm Pr}(-s_0) = {1}/{ 3}, \hspace{0.15cm} p_{\rm 0} = {\rm Pr}(0) = {1}/{ 3}, \hspace{0.15cm} p_{\rm +} = {\rm Pr}(+s_0) ={1}/{ 3}\hspace{0.05cm}.$$

Die Entscheiderschwellen liegen vorerst mittig bei $E_{–} = \, –s_0/2$ und $E_{+} = +s_0/2$.

Ab der Teilaufgabe (3) gelten für die Symbolwahrscheinlichkeiten $p_{–} = p_+ = 1/4$ und $p_0 = 1/2$, wie in der Grafik dargestellt. Für diese Konstellation soll durch Variation der Entscheiderschwellen $E_{–}$ und $E_+$ die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ minimiert werden.

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel Redundanzfreie Codierung.
• Für die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ eines $M$–stufigen Nachrichtenübertragungssystems mit gleichwahrscheinlichen Eingangssymbolen und Schwellenwerten genau in der Mitte zwischen zwei benachbarten Amplitudenstufen gilt:

$$p_{\rm S} = \frac{ 2 \cdot (M-1)}{M} \cdot {\rm Q} \left( {\frac{s_0}{(M-1) \cdot \sigma_d}}\right) \hspace{0.05cm}.$$

• Die Fehlerwahrscheinlichkeitswerte gemäß der ${\rm Q}$– bzw. der ${\rm erfc}$–Funktion können Sie mit folgendem Interaktionsmodul numerisch ermitteln: Komplementäre Gaußsche Fehlerfunktionen
• Verwenden Sie zur Überprüfung der Ergebnisse das Berechnungsmodul Symbolfehlerwahrscheinlichkeit von Digitalsystemen
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit dem (normierten) Rauscheffektivwert $\sigma_d/s_0 = 0.25$ bei gleichwahrscheinlichen Symbolen?

$p_0 = 1/3, \sigma_d = 0.25 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

2

Wie ändert sich die Symbolfehlerwahrscheinlichkeit mit $\sigma_d/s_0 = 0.5$?

$p_0 = 1/3, \sigma_d = 0.5 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

3

Welcher Wert ergibt sich mit $p_{–} = p_+ = 0.25$ und $p_0 = 0.5$?

$p_0 = 1/2, \sigma_d = 0.5 \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

4

Bestimmen Sie die optimalen Schwellen $E_+$ und $E_{–} = \, –E_+$ für $p_0 = 1/2$.

$p_0 = 1/2, \sigma_d = 0.5 \text{:} \hspace{0.4cm} E_{\rm +, \ opt} \ = \ $

5

Welche Fehlerwahrscheinlichkeit ergibt sich bei optimalen Schwellen?

${\rm optimale \ Schwellen} \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

6

Wie lauten die optimalen Schwellenwerte für $p_0 = 0.2$ und $p_{–} = p_+ = 0.4$?

$p_0 = 0.2, \sigma_d = 0.5 \text{:} \hspace{0.4cm} E_{\rm +, \ opt} \ = \ $

7

Welche Symbolfehlerwahrscheinlichkeit ergibt sich nun? Interpretation.

${\rm optimale \ Schwellen} \text{:} \hspace{0.4cm} p_{\rm S} \ = \ $ $\ \%$

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)