Aufgaben:Aufgabe 4.4: Extrinsische L–Werte beim SPC: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
[[Datei:P_ID2993__KC_A_4_4_v1.png|right|frame|Hilfstabelle]] | [[Datei:P_ID2993__KC_A_4_4_v1.png|right|frame|Hilfstabelle]] | ||
| + | Wir betrachten nochmals den [[Single Parity–check Code]]. Bei einem solchen SPC (n, n–1, 2) stammen von den $n$ Bits eines Codewortes $\underline{x}$ die ersten $k = n \, –1 \ \rm Bits$ von der Quellenfolge $\underline{u}$ und es wird nur ein einziges Prüfbit $p$ hinzugefügt, und zwar derart, dass die Anzahl der Einsen im Codewort geradzahlig ist: | ||
| + | :$$\underline{x} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} x_2, \hspace{0.03cm} ... \hspace{0.08cm} , x_{n-1}, \hspace{0.03cm} x_n \hspace{0.03cm} \big ) = | ||
| + | \big ( \hspace{0.03cm}u_1, \hspace{0.03cm} u_2, \hspace{0.03cm} ... \hspace{0.08cm} , u_{k}, \hspace{0.03cm} p \hspace{0.03cm} \big )\hspace{0.03cm}. $$ | ||
| + | |||
| + | Die extrinsische Information über das $i$–te Codebit wird über alle anderen Symbole $(j ≠ i)$ gebildet. Deshalb schreiben wir für das um ein Bit kürzere Codewort: | ||
| + | :$$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} ... \hspace{0.08cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.03cm} ... \hspace{0.08cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$ | ||
| + | |||
| + | Der extrinsische $L$–Wert über das $i$–te Codesymbol lautet mit dem [[Hamming–Gewicht]] "w_{\rm H}$ der verkürzten Folge $\underline{x}^{-i}$: | ||
| + | :$$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Ist die Wahrscheinlichkeit im Zähler größer als die im Nenner, so ist $L_{\rm E}(i) > 0$ und damit wird auch der Aposteriori–$L$–Wert $L_{\rm APP}(i) = L_{\rm A}(i) + L_{\rm E}(i)$ vergrößert, das heißt tendenziell in Richtung des Symbols $x_i = 0$ beeinflusst. Andernfalls (bei $L_{\rm E}(i) < 0$) spricht aus Sicht der anderen Symbole $(j ≠ i)$ vieles dafür, dass $x_i = 1$ ist. | ||
| + | |||
| + | Behandelt wird ausschließlich der SPC (4, 3, 4), wobei für die Wahrscheinlichkeiten $p_i = {\rm Pr}(x_i = 1)$ gilt: | ||
| + | :$$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} | ||
| + | p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} | ||
| + | p_3 = 0.3 \hspace{0.05cm}, \hspace{0.3cm} | ||
| + | p_4 = 0.6 \hspace{0.05cm}.$$ | ||
| + | |||
| + | Daraus ergeben sich die Apriori–$L$–Werte zu: | ||
| + | :$$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} | ||
| + | \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} | ||
| + | \right ] | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | ''Hinweise:'' | ||
| + | * Die Aufgabe gehört zum Themengebiet des Kapitels [[http://www.lntwww.de/Kanalcodierung/Soft%E2%80%93in_Soft%E2%80%93out_Decoder| Soft–in Soft–out Decoder]] | ||
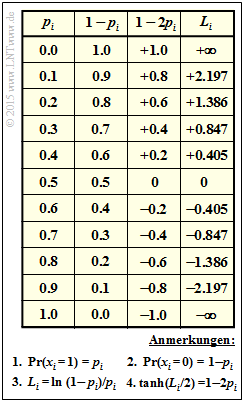
| + | * In der oberen Tabelle sind für $p_i = 0$ bis $p_i = 1$ mit Schrittweite $0.1$ angegeben: | ||
| + | ** die Wahrscheinlichkeit $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ ⇒ Spalte 2, | ||
| + | ** die Werte für $1 - 2p_i$ ⇒ Spalte 3, | ||
| + | ** die Apriori–$L$–Werte $L_i = \ln [(1 - p_i)/p_i] = L_{\rm A}(i)$ ⇒ Spalte 4. | ||
Version vom 7. Dezember 2017, 22:55 Uhr
Wir betrachten nochmals den Single Parity–check Code. Bei einem solchen SPC (n, n–1, 2) stammen von den $n$ Bits eines Codewortes $\underline{x}$ die ersten $k = n \, –1 \ \rm Bits$ von der Quellenfolge $\underline{u}$ und es wird nur ein einziges Prüfbit $p$ hinzugefügt, und zwar derart, dass die Anzahl der Einsen im Codewort geradzahlig ist:
- $$\underline{x} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} x_2, \hspace{0.03cm} ... \hspace{0.08cm} , x_{n-1}, \hspace{0.03cm} x_n \hspace{0.03cm} \big ) = \big ( \hspace{0.03cm}u_1, \hspace{0.03cm} u_2, \hspace{0.03cm} ... \hspace{0.08cm} , u_{k}, \hspace{0.03cm} p \hspace{0.03cm} \big )\hspace{0.03cm}. $$
Die extrinsische Information über das $i$–te Codebit wird über alle anderen Symbole $(j ≠ i)$ gebildet. Deshalb schreiben wir für das um ein Bit kürzere Codewort:
- $$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} ... \hspace{0.08cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.03cm} ... \hspace{0.08cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$
Der extrinsische $L$–Wert über das $i$–te Codesymbol lautet mit dem Hamming–Gewicht "w_{\rm H}$ der verkürzten Folge $\underline{x}^{-i}$: :'"`UNIQ-MathJax5-QINU`"' Ist die Wahrscheinlichkeit im Zähler größer als die im Nenner, so ist $L_{\rm E}(i) > 0$ und damit wird auch der Aposteriori–$L$–Wert $L_{\rm APP}(i) = L_{\rm A}(i) + L_{\rm E}(i)$ vergrößert, das heißt tendenziell in Richtung des Symbols $x_i = 0$ beeinflusst. Andernfalls (bei $L_{\rm E}(i) < 0$) spricht aus Sicht der anderen Symbole $(j ≠ i)$ vieles dafür, dass $x_i = 1$ ist. Behandelt wird ausschließlich der SPC (4, 3, 4), wobei für die Wahrscheinlichkeiten $p_i = {\rm Pr}(x_i = 1)$ gilt: :'"`UNIQ-MathJax6-QINU`"' Daraus ergeben sich die Apriori–$L$–Werte zu: :'"`UNIQ-MathJax7-QINU`"' ''Hinweise:'' * Die Aufgabe gehört zum Themengebiet des Kapitels [[http://www.lntwww.de/Kanalcodierung/Soft%E2%80%93in_Soft%E2%80%93out_Decoder| Soft–in Soft–out Decoder]] * In der oberen Tabelle sind für $p_i = 0$ bis $p_i = 1$ mit Schrittweite $0.1$ angegeben: ** die Wahrscheinlichkeit $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ ⇒ Spalte 2, ** die Werte für $1 - 2p_i$ ⇒ Spalte 3, ** die Apriori–$L$–Werte $L_i = \ln [(1 - p_i)/p_i] = L_{\rm A}(i)$ ⇒ Spalte 4.
Fragebogen
Musterlösung