Aufgaben:Aufgabe 1.1Z: Tiefpass 1. und 2. Ordnung

• Zurück zum Buch

Vorgegebene Dämpfungs– und Phasenfunktion

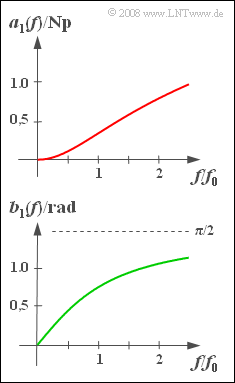
Die einfachste Form eines Tiefpasses – zum Beispiel realisierbar als ein RC–Tiefpass entsprechend Aufgabe 1.1 – hat folgenden Frequenzgang:

$$H_{\rm 1}(f) = \frac{1}{1+{\rm j}\cdot f/f_0}.$$

Man spricht dann von einem Tiefpass erster Ordnung. In der Grafik dargestellt sind für dieses Filter

• oben der Dämpfungsverlauf $a_1(f)$,
• unten der Phasenverlauf $b_1(f)$ .

Entsprechend gilt für einen Tiefpass $n$–ter Ordnung die folgende Definitionsgleichung:

$$H_n(f) = H_{\rm 1}(f)^n.$$

In dieser Aufgabe sollen – ausgehend von den Funktionen $a_1(f)$ und $b_1(f)$ für den Tiefpass erster Ordnung – der Dämpfungs– und Phasenverlauf eines Tiefpasses höherer Ordnung analysiert werden. Allgemein gilt: $$H(f) = {\rm e}^{-a(f) - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Systembeschreibung im Frequenzbereich.

• Zwischen dem Np– und dem dB–Wert eines Amplitudenwertes $|H| = 1/x$ besteht folgender Zusammenhang:

$$a_{\rm Np} = \ln (x) = \ln (10) \cdot \lg (x) = \frac{\ln (10)}{20} \cdot a_{\rm dB} \approx 0.11513 \cdot a_{\rm dB}.$$

• Berücksichtigen Sie weiter, dass für zwei komplexe Größen $z_1$ und $z_2$ folgende Gleichungen gelten:

$$|z_1 \cdot z_2| = |z_1| \cdot |z_2|, \hspace{0.5 cm}{\rm arc}\hspace{0.05 cm}(z_1 \cdot z_2) = {\rm arc}\hspace{0.05 cm}(z_1) + {\rm arc}\hspace{0.05 cm}(z_2).$$

Fragebogen

1

Berechnen Sie den Dämpfungsverlauf $a_1(f)$ eines Tiefpasses erster Ordnung in dB. Welche dB–Werte ergeben sich bei $f = f_0$ und $f = 2f_0$?

$a_1(f = f_0)\ = \ $  $\text{dB}$

$a_1(f = 2f_0)\ = \ $  $\text{dB}$

2

Berechnen Sie den Phasenverlauf $b_1(f)$. Welche Werte in Radian (rad) erhält man bei $f = f_0$ und $f = 2f_0$?

$b_1(f = f_0)\ = \ $  $\text{rad}$

$b_1(f = 2f_0)\ = \ $  $\text{rad}$

3

Welchen Dämpfungsverlauf $a_n(f)$ hat ein Tiefpass $n$–ter Ordnung? Welche dB–Werte erhält man mit $n = 2$ für $f = f_0$ bzw. $f = \: –2f_0$?

$a_2(f = f_0)\ = \ $  $\text{dB}$

$a_2(f = -2f_0)\ = \ $  $\text{dB}$

4

Berechnen Sie die Phasenfunktion $b_2(f)$ eines Tiefpasses zweiter Ordnung. Welche Werte (in Radian) erhält man für $f = f_0$ und $f = \: –2f_0$?

$b_2(f = f_0)\ = \ $  $\text{rad}$

$b_2(f = -2f_0)\ = \ $  $\text{rad}$

Musterlösung

Musterlösung

(1)  Der Amplitudengang des Tiefpasses erster Ordnung lautet:

$$|H_{\rm 1}(f)| = \frac{1}{\sqrt{1+ (f/f_0)^2}}.$$

Damit erhält man den Dämpfungsverlauf in Neper (Np):

$$a_1(f) = \ln \frac{1}{|H_1(f)|} = {1}/{2} \cdot \ln \left[1 + ({f}/{f_0})^2 \right] \Rightarrow a_1(f = f_0) = 0.34657 \hspace{0.1 cm}{\rm Np},\hspace{0.5 cm}a_1(f = 2 f_0) = 0.804719 \hspace{0.1 cm}{\rm Np}.$$

Die entsprechenden dB–Werte erhält man durch Multiplikation mit $1/0.11513 = 8.68589$ und führt zu den Ergebnissen $ \underline{3.01 \: {\rm dB} ≈ 3 \: {\rm dB}}$ für $ f = f_0$ und $ \underline{6.99 \: {\rm dB}}$ für $ f = 2f_0$. Beim Tiefpass erster Ordnung beträgt somit die 3dB–Grenzfrequenz $f_{\rm G} = f_0$.

(2)  Der Frequenzgang $H_1(f)$ kann auch nach Real– und Imaginärteil getrennt dargestellt werden:

$$H_{\rm 1}(f) = \frac{1}{ {1+ (f/f_0)^2} } - {\rm j} \cdot \frac{f/f_0}{ {1+ (f/f_0)^2} }.$$

Damit ergibt sich für den Phasengang:

$$b_1(f) = - \arctan \hspace{0.1cm} ( {\rm Im} /{\rm Re} ) = \arctan \hspace{0.1cm} ({f}/{f_0}).$$

Für $f = f_0$ erhält man $\arctan(1) = π/4 \rm \underline{\: = 0.786 \: rad}$, für $f = 2f_0$ den Wert $\arctan(2) \rm \underline{\: = 1.108 \: rad}$.

(3)  Für den Amplitudengang eines Tiefpasses $n$–ter Ordnung gilt:

$$|H_n(f)| = |H_{\rm 1}(f)|^n.$$

Bezüglich der (logarithmischen) Dämpfungsfunktion wird aus der $n$–fachen Multiplikation die $n$–fache Summe:

$$a_n(f) = n \cdot a_1(f)= {n}/{2} \cdot \ln \left[ 1 + ({f}/{f_0})^2 \right].$$

Für den Tiefpass zweiter Ordnung ergibt sich daraus als Sonderfall:

$$a_2(f) = \ln \left[ 1 + ({f}/{f_0})^2 \right]= 2 \cdot a_1(f).$$

Die dB–Werte lauten nun:

• $ \underline{6.02 \: {\rm dB} ≈ 6 \: {\rm dB}}$ für $f = ±f_0$,
• $\rm \underline{13.98 \: {\rm dB} ≈ 14 \: {\rm dB}}$ für $f = ±2f_0$.

Damit ist offensichtlich, dass für $n > 1$ der Parameter $f_0$ nicht mehr die 3 dB–Grenzfrequenz $f_{\rm G}$ angibt. Für $n = 2$  ⇒  „Tiefpass zweiter Ordnung” gilt vielmehr der Zusammenhang:   ${f_{\rm G} } = {f_0}/\sqrt{2}$.

(4)  Auch bezüglich der Phasenfunktion gilt:

$$b_n(f) = n \cdot b_1(f), \hspace{0.3 cm} b_2(f) = 2 \cdot b_1(f).$$

Beim Tiefpass zweiter Ordnung sind somit alle Phasenwerte zwischen $±π$ möglich. Insbesondere ist

• $b_2(f = f_0) = π/2 \rm \underline{\: = 1.571 \: rad}$,
• $b_2(f = 2f_0) = \rm 2.216 \: rad$.

Da die Phase eine ungerade Funktion ist, gilt hier:   $b_2(f = \: –2f_0) = \rm \underline{–2.216 \: rad}$.