Aufgaben:Aufgabe 4.6: k-Parameter und Alpha-Parameter

• Zurück zum Buch

Dämpfungsmaß einer 0.5 mm Doppelader mit $k$– und $\alpha$-Parameter

Für symmetrische Kupfer–Doppeladern findet man in [PW95] die folgende empirische Formel, gültig für den Frequenzbereich $0 \le f \le 30 \ \rm MHz$:

$$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3} , \hspace{0.15cm} f_0 = 1\,{\rm MHz} .$$

Dagegen ist das Dämpfungsmaß eines Koaxialkabels meist in der folgenden Form angegeben:

$$\alpha_{\rm II}(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}\hspace{0.05cm}.$$

Insbesondere zur Berechnung von Impulsantwort und Rechteckantwort ist es von Vorteil, auch für die Kupfer–Doppeladern die zweite Darstellungsform mit den Kabelparametern $\alpha_0$, $\alpha_1$ und $\alpha_2$ anstelle der Beschreibung durch $k_1$, $k_2$ und $k_3$ zu wählen.

Für die Umrechnung geht man dabei wie folgt vor:

• Aus obigen Gleichungen ist offensichtlich, dass der die Gleichsignaldämpfung charakterisierende Koeffizient $\alpha_0 = k_1$ ist.
• Zur Bestimmung von $\alpha_1$ und $\alpha_2$ wird davon ausgegangen, dass der mittlere quadratische Fehler im Bereich einer vorgegebenen Bandbreite $B$ minimal sein soll:

$${\rm E}[\varepsilon^2(f)] = \int_{0}^{ B} \left [ \alpha_{\rm II} (f) - \alpha_{\rm I} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$

• Die Differenz $\varepsilon^2(f)$ und der mittlere quadratische Fehler ${\rm E}[\varepsilon^2(f)]$ ergeben sich dabei wie folgt:

$$\varepsilon^2(f) = \left [ \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f} - k_2 \cdot (f/f_0)^{k_3}\right ]^2 =\alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm} f^2 + 2 \alpha_1 \alpha_2 \hspace{0.05cm}\cdot\hspace{0.05cm} f^{1.5} + \alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm} f + k_2^2\hspace{0.05cm}\cdot\hspace{0.05cm} \frac{f^{2k_3}}{f_0^{2k_3}} - 2 k_2 \alpha_1 \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{f^{k_3+1}} {f_0^{k_3}}-{2 k_2 \alpha_2} \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{f^{k_3+0.5}}{f_0^{k_3}}$$

$$\Rightarrow \hspace{0.3cm}{\rm E}[\varepsilon^2(f)] = \alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm}\frac{B^3}{3} + \frac{4}{5} \hspace{0.05cm}\cdot\hspace{0.05cm}\alpha_1 \alpha_2 \hspace{0.05cm}\cdot\hspace{0.05cm}B^{2.5} + \alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{B^2}{2} + \frac{k_2^2}{2k_3 +1} \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{B^{2k_3+1}}{f_0^{2k_3}} - \hspace{0.15cm} \frac{2 k_2 \alpha_1}{k_3 + 2} \hspace{0.05cm}\cdot\hspace{0.05cm} $$

Diese Gleichung beinhaltet die zu verrechnenden Kabelparameter $\alpha_1$, $\alpha_2$, $k_2$ und $k_3$ sowie die Bandbreite $B$, innerhalb derer die Approximation gültig sein soll.

• Durch Nullsetzen der Ableitungen von ${\rm E}[\varepsilon^2(f)]$ nach $\alpha_1$ bzw. $\alpha_2$ erhält man zwei Gleichungen für die bestmöglichen Koeffizienten $\alpha_1$ und $\alpha_2$, die den mittleren quadratischen Fehler minimieren. Diese lassen sich in folgender Form darstellen:

$$\frac{{\rm d}\,{\rm E}[\varepsilon^2(f)]}{{\rm d}\,{\alpha_1}} = 0 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \alpha_1 + C_1 \cdot \alpha_2 + C_2 = 0 \hspace{0.05cm} ,$$

$$\frac{{\rm d}\,{\rm E}[\varepsilon^2(f)]}{{\rm d}\,{\alpha_2}} = 0 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \alpha_1 + D_1 \cdot \alpha_2 + D_2 = 0 \hspace{0.05cm} . $$

• Aus der Gleichung $C_1 \cdot \alpha_2 + C_2 = D_1 \cdot \alpha_2 + D_2$ lässt sich daraus der Koeffizient $\alpha_2$ berechnen und anschließend aus jeder der beiden oberen Gleichungen der Koeffizient $\alpha_1$.

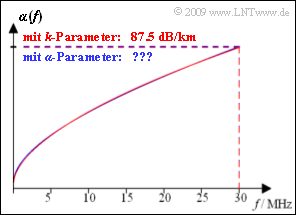
Die Grafik zeigt das Dämpfungsmaß für eine Kupferdoppelader mit 0.5 mm Durchmesser, deren $k$–Parameter lauten:

$$k_1 = 4.4\, {\rm dB}/{\rm km} \hspace{0.05cm}, \hspace{0.2cm} k_2 = 10.8\, {\rm dB}/{\rm km}\hspace{0.05cm}, \hspace{0.2cm}k_3 = 0.60\hspace{0.05cm} \hspace{0.05cm}.$$

• Die rote Kurve zeigt die damit berechnete Funktion $\alpha(f)$. Für $f = 30 \ \rm MHz$ ergibt sich das Dämpfungsmaß $\alpha(f) 87.5 \ \rm dB/km$.
• Die blaue Kurve gibt die Approximation mit den $\alpha$ndash;Koeffizienten an. Diese ist von der roten Kurve innerhalb der Zeichengenauigkeit fast nicht zu unterscheiden.

Hinweise:

• Die Aufgabe gehört zum Kapitel Eigenschaften von Kupfer–Doppeladern.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Sie können zur Überprüfung Ihrer Ergebnisse das Interaktionsmodul Dämpfung von Kupferkabeln benutzen.
• [PW95] kennzeichnet folgenden Literaturhinweis:

Pollakowski, P.; Wellhausen, H.-W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Deutsche Telekom AG, Forschungs- und Technologiezentrum Darmstadt, 1995.

Fragebogen

1

Berechnen Sie die Parameter $C_1$ und $C_2$ der Gleichung $\alpha_1 + C_1 \cdot \alpha_2 + C_2 = 0$, die sich aus der Ableitung ${\rm dE[\text{...}]/d}\alpha_1$ ergeben.
Welche Ergebnisse sind zutreffend?

	$C_1 = 6/5 \cdot B^{-0.5}$,
	$C_1 = 5/4 \cdot B^{-0.5}$,
	$C_1 = 4/3 \cdot B^{2}$,
	$C_2 = -4/3 \cdot B^{-2$}$,
	$C_2 = -5/2 \cdot k_2/(k_3 +1.5) \cdot B^{k_3 -1} \cdot f_0^{-k_3}$,
	$C_2 = -3 \cdot k_2/(k_3 +2) \cdot B^{k_3 -1} \cdot f_0^{-k_3}$.

2

Berechnen Sie die Parameter $D_1$ und $D_2$ der Gleichung $ \alpha_1 + D_1 \cdot \alpha_2 + D_2 = 0$, die sich aus der Ableitung ${\rm dE[text{...}]/d}\alpha_2$ ergeben.
Welche Ergebnisse sind zutreffend?

	$D_1 = 6/5 \cdot B^{-0.5}$,
	$D_1 = 5/4 \cdot B^{-0.5}$,
	$D_1 = 4/3 \cdot B^{2}$,
	$D_2 = -4/3 \cdot B^{-2}$,
	$D_2 = -5/2 \cdot k_2/(k_3 +1.5) \cdot B^{k_3 -1} \cdot f_0^{-k_3}$,
	$D_2 = -3 \cdot k_2/(k_3 +2) \cdot B^{k_3 -1} \cdot f_0^{-k_3}$.

3

Berechnen Sie die Koeffizienten $\alpha_1$ und $\alpha_2$ für die vorgegebenen $k_2$ und $k_3$.
Welche der folgenden Aussagen sind zutreffend?

	Für $k_3=1.0$ gilt $\alpha_1 = k_2/f_0$ und $\alpha_2 = 0$.
	Für $k_3=0.5$ gilt $\alpha_1 = 0$, und $\alpha_2 = k_2/f_0^{0.5}$.

4

Ermitteln Sie die Koeffizienten $\alpha_1$ und $\alpha_2$ zahlenmäßig für die Approximationsbandbreite $B = 30 \ \rm MHz$.

$\alpha_1 \ = \ $ $\ \rm dB/(km\ \cdot \ MHz)$

$\alpha_2 \ =\ $ $\ \rm dB/(km\ \cdot \ \sqrt{\rm MHz})$

5

Berechnen Sie mit den $\alpha$ndash;Parametern das Dämpfungsmaß bei $f = 30\ \rm MHz$.

$\alpha_{\rm II}(f = 30\ \rm MHz) \ = \ $ $\ \rm dB/km$

Musterlösung

Musterlösung

(1)  Richtig sind die Lösungsvorschläge 1 und 6:

• Die Ableitung des angegebenen Erwartungswertes nach $\alpha_1$ ergibt:

$$\frac{{\rm d}\,{\rm E}[\varepsilon^2(f)]}{{\rm d}\,{\alpha_1}} = \frac{2}{3}\cdot B^3 \cdot \alpha_1 + \frac{4}{5}\cdot B^{2.5} \cdot \alpha_2 - \frac{2 k_2 }{k_3 + 2} \cdot \frac{B^{k_3+2}}{f_0^{k_3}}= 0 \hspace{0.05cm} .$$

• Durch Nullsetzen und Division durch $2B^2/3$ erhält man daraus:

$$\alpha_1 + \frac{6}{5}\cdot B^{-0.5} \cdot \alpha_2 - \frac{3 k_2 }{k_3 +2} \cdot \frac{B^{k_3-1}}{f_0^{k_3}}= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} C_1 = \frac{6}{5}\cdot B^{-0.5} \hspace{0.05cm} , \hspace{0.5cm} C_2 = - \frac{3 k_2 }{k_3 +2} \cdot \frac{B^{k_3-1}}{f_0^{k_3}} \hspace{0.05cm} .$$

(2)  Richtig sind die Lösungsvorschläge 2 und 5:

• Bei gleicher Vorgehensweise wie in der Teilaufgabe (1) erhält man:

$$\frac{{\rm d}\,{\rm E}[\varepsilon^2(f)]}{{\rm d}\,{\alpha_2}} = \frac{4}{5}\cdot B^{2.5} \cdot \alpha_1 + B^{2} \cdot \alpha_2 - \frac{2 k_2 }{k_3 + 1.5} \cdot \frac{B^{k_3+1.5}}{f_0^{k_3}}= 0$$

$$\Rightarrow \hspace{0.3cm} \alpha_1 + \frac{5}{4}\cdot B^{-0.5} \cdot \alpha_2 - \frac{2.5 \cdot k_2 }{k_3 +1.5} \cdot \frac{B^{k_3-1}}{f_0^{k_3}}= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_1 = \frac{5}{4}\cdot B^{-0.5} \hspace{0.05cm} , \hspace{0.3cm}D_2 = - \frac{2.5 \cdot k_2 }{k_3 +1.5} \cdot \frac{B^{k_3-1}}{f_0^{k_3}} \hspace{0.05cm} .$$

(3)  Aus $C_1 \cdot \alpha_2 + C_2 = D_1 \cdot \alpha_2 + D_2$ ergibt sich eine lineare Gleichung für $\alpha_2$. Mit dem Ergebnis aus (2) kann hierfür geschrieben werden:

$$\alpha_2 = \frac{D_2 - C_2}{C_1 - D_1} = \frac{- \frac{2.5 \cdot k_2 }{k_3 +1.5} \cdot \frac{B^{k_3-1}}{f_0^{k_3}} + \frac{3 k_2 }{k_3 +2} \cdot \frac{B^{k_3-1}}{f_0^{k_3}}}{{6}/{5}\cdot B^{-0.5} - {5}/{4}\cdot B^{-0.5}} = \frac{- {2.5 \cdot k_2 }\cdot(k_3 +2) + {3 k_2 }\cdot (k_3 +1.5) }{({6}/{5} - {5}/{4})(k_3 +1.5)(k_3 +2)} \cdot \frac{B^{k_3-0.5}}{f_0^{k_3}}$$

$$ \Rightarrow \hspace{0.3cm}\alpha_2 = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}} \hspace{0.05cm} .$$

Für den Parameter $\alpha_1$ gilt dann:

$$\alpha_1 = - C_1 \cdot \alpha_2 - C_2 = -\frac{6}{5}\cdot B^{-0.5} \cdot 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}} +\frac{3 k_2 }{k_3 +2} \cdot \frac{B^{k_3-1}}{f_0^{k_3}}$$

$$ \Rightarrow \hspace{0.3cm}\alpha_1 = (B/f_0)^{k_3 -1}\cdot \frac{-12 \cdot (1-k_3) + 3 \cdot (k_3 + 1.5)}{(k_3 + 1.5)(k_3 + 2)} \cdot \frac {k_2}{f_0} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\alpha_1 =15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{f_0}\hspace{0.05cm} .$$

Die beiden Lösungsvorschläge sind richtig. Unabhängig von der Bandbreite erhält man für $k_3 = 1$:

$$\alpha_1 = (B/f_0)^{k_3 -1}\cdot \frac{15 \cdot (k_3 -0.5)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{f_0} = \frac{15 \cdot 0.5}{2.5 \cdot 3}\cdot \frac {k_2}{f_0} \hspace{0.15cm}\underline{ = {k_2}/{f_0}}\hspace{0.05cm} ,$$

$$ \alpha_2 = (B/f_0)^{k_3 -0.5}\cdot \frac{10 \cdot (1-k_3)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}}\hspace{0.15cm}\underline{= 0} \hspace{0.05cm} .$$

Dagegen ergibt sich für $k_3 = 0.5$:

$$\alpha_1 = (B/f_0)^{k_3 -1}\cdot \frac{15 \cdot (k_3 -0.5)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{f_0} \hspace{0.15cm}\underline{= 0}\hspace{0.05cm} ,$$

$$ \alpha_2 = (B/f_0)^{k_3 -0.5}\cdot \frac{10 \cdot (1-k_3)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}}= \frac{10 \cdot 0.5}{2 \cdot 2.5}\cdot \frac {k_2}{\sqrt{f_0}} = \hspace{0.15cm}\underline{ {k_2}/{\sqrt{f_0}}} \hspace{0.05cm} .$$

(4)  Für die beiden Koeffizienten gilt mit $k_2 = 10.8 \ \rm dB/km$, $k_3 = 0.6 \ \rm dB/km$ und $B/f_0 = 30$:

$$\alpha_1 = (B/f_0)^{k_3 -1}\cdot \frac{15 \cdot (k_3 -0.5)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{f_0} = 30^{-0.4}\cdot \frac{15 \cdot 0.1}{2.1 \cdot 2.6}\cdot \frac {10.8 \, {\rm dB/km} }{1 \, {\rm MHz}} \hspace{0.15cm}\underline{ \approx 0.761\, {{\rm dB} }/{({\rm km \cdot MHz})}} \hspace{0.05cm} ,$$

$$ \alpha_2 = (B/f_0)^{k_3 -0.5}\cdot \frac{10 \cdot (1-k_3)}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0}}= \frac {k_2}{\sqrt{f_0}} = 30^{0.1}\cdot \frac{10 \cdot 0.4}{2.1 \cdot 2.6}\cdot \frac {10.8 \, {\rm dB/km} }{1 \, {\rm MHz^{0.5}}} \hspace{0.15cm}\underline{ \approx 11.1\, {{\rm dB} }/{({\rm km \cdot \sqrt{MHz}}})}\hspace{0.05cm} .$$

(5)  Entsprechend der angegebenen Gleichung $\alpha_{\rm II}(f$) gilt damit auch:

$$\alpha_{\rm II}(f = 30 \, {\rm MHz}) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f} = \left [ \hspace{0.05cm} 4.4 + 0.761 \cdot 30 + 11.1 \cdot \sqrt {30}\hspace{0.05cm} \right ]\frac {\rm dB}{\rm km } \hspace{0.15cm}\underline{\approx 88.1\, {\rm dB}/{\rm km }} \hspace{0.05cm}.$$