Aufgaben:Aufgabe 1.2Z: 3D–Darstellung von Codes: Unterschied zwischen den Versionen
Aus LNTwww
K (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Zeile 2: | Zeile 2: | ||
}} | }} | ||
| − | [[Datei:P_ID2400__KC_Z_1_2.png|right|frame|Raum $\rm GF(2^3)$ und Code der Länge $n = 3$]] | + | [[Datei:P_ID2400__KC_Z_1_2.png|right|frame|Raum $\rm GF(2^3)$ und <br>Code der Länge $n = 3$]] |
| − | Codes zur Fehlererkennung bzw. Fehlererkorrektur lassen sich sehr anschaulich im $n$–dimensionalen Raum darstellen. Wir beschränken uns hier auf binäre Codes der Länge $n = 3$: | + | Codes zur Fehlererkennung bzw. Fehlererkorrektur lassen sich sehr anschaulich im $n$–dimensionalen Raum darstellen. Wir beschränken uns hier auf binäre Codes der Länge $n = 3$: |
:$$\underline{x} = (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\hspace{0.5cm} x_i = \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$ | :$$\underline{x} = (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\hspace{0.5cm} x_i = \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$ | ||
Allgemein gilt bei der Blockcodierung: | Allgemein gilt bei der Blockcodierung: | ||
| − | *Das Informationswort $\underline{u} = (u_{1}, u_{2}, \ \text{...} , \ u_{k})$ wird eindeutig in das Codewort $\underline{x} =(x_{1}, x_{2}, \ \text{...} , \ , x_{n})$ überführt. | + | *Das Informationswort $\underline{u} = (u_{1}, u_{2}, \ \text{...} , \ u_{k})$ wird eindeutig in das Codewort $\underline{x} =(x_{1}, x_{2}, \ \text{...} , \ , x_{n})$ überführt. |
| − | *Die Coderate beträgt $R = k/n$. | + | *Die Coderate beträgt $R = k/n$. |
| − | *Die Hamming–Distanz $d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')$ zwischen zwei Codeworten $x ∈ \mathcal{C}$ und $x\hspace{0.05cm}' ∈ \mathcal{C}$ gibt die Anzahl der Bitpositionen an, in denen sich $x$ und $x\hspace{0.05cm}'$ unterscheiden. | + | *Die Hamming–Distanz $d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')$ zwischen zwei Codeworten $x ∈ \mathcal{C}$ und $x\hspace{0.05cm}' ∈ \mathcal{C}$ gibt die Anzahl der Bitpositionen an, in denen sich $x$ und $x\hspace{0.05cm}'$ unterscheiden. |
| − | *Die Minimaldistanz $d_{\rm min} = {\rm min}[d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')]$ ist ein Maß für die Korrekturfähigkeit eines Codes. | + | *Die Minimaldistanz $d_{\rm min} = {\rm min}\big[d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')\big]$ ist ein Maß für die Korrekturfähigkeit eines Codes. |
| − | *Es können $e =d_{\rm min} – 1$ Fehler erkannt und $t =(d_{\rm min} – 1)/2$ Fehler korrigiert werden. Die letzte Aussage gilt allerdings nur für ungerades $d_{\rm min}$. | + | *Es können $e =d_{\rm min} – 1$ Fehler erkannt und $t =(d_{\rm min} – 1)/2$ Fehler korrigiert werden. |
| + | *Die letzte Aussage gilt allerdings nur für ungerades $d_{\rm min}$. | ||
| + | |||
| + | |||
| + | |||
''Hinweise'': | ''Hinweise'': | ||
| − | *Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Zielsetzung_der_Kanalcodierung|Zielsetzung der Kanalcodierung]]. | + | *Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Zielsetzung_der_Kanalcodierung|Zielsetzung der Kanalcodierung]]. |
| − | *Zusätzlich werden einige einfache Fragen zum Kapitel [[Kanalcodierung/Beispiele_binärer_Blockcodes|Beispiele binärer Blockcodes]] vorweg genommen. | + | *Zusätzlich werden einige einfache Fragen zum Kapitel [[Kanalcodierung/Beispiele_binärer_Blockcodes|Beispiele binärer Blockcodes]] vorweg genommen. |
| Zeile 26: | Zeile 30: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Aussagen gelten, wenn alle Punkte in $\rm GF(2^3)$ belegt sind? | + | {Welche Aussagen gelten, wenn alle Punkte in $\rm GF(2^3)$ belegt sind? |
|type="[]"} | |type="[]"} | ||
| − | + Es gilt die Zuordnung $\underline{u} = (u_{1}, u_{2}, u_{3})$ → $\underline{ | + | + Es gilt die Zuordnung $\underline{u} = (u_{1}, u_{2}, u_{3})$ → $\underline{x} = (x_{1}, x_{2},x_{3})$. |
| − | - Es gilt die Identität $\underline{x} = \underline{u}$. | + | - Es gilt die Identität $\underline{x} = \underline{u}$. |
| − | + Die Coderate ist $R = 1$. | + | + Die Coderate ist $R = 1$. |
| − | -Die Minimaldistanz zwischen zwei Codeworten ist $d_{\rm min} = 2$. | + | -Die Minimaldistanz zwischen zwei Codeworten ist $d_{\rm min} = 2$. |
{Welche Aussagen gelten für einen (3, 2, 2)–Blockcode? | {Welche Aussagen gelten für einen (3, 2, 2)–Blockcode? | ||
|type="[]"} | |type="[]"} | ||
| − | + Code $\mathcal{C}_{1} = \{(0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0)\}$ ist möglich. | + | + Code $\mathcal{C}_{1} = \{(0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0)\}$ ist möglich. |
| − | - Code $\mathcal{C}_{2} = \{(0, 0, 1), (0, 1, 0), (1, 0, 0), (1, 1, 1)\}$ ist möglich. | + | - Code $\mathcal{C}_{2} = \{(0, 0, 1), (0, 1, 0), (1, 0, 0), (1, 1, 1)\}$ ist möglich. |
| − | + Code $\mathcal{C}_{3} = \{(0, 0, 0), (0, 1, 1), (1, 0, 0), (1, 1, 1)\}$ ist möglich. | + | + Code $\mathcal{C}_{3} = \{(0, 0, 0), (0, 1, 1), (1, 0, 0), (1, 1, 1)\}$ ist möglich. |
| − | {Welche Eigenschaften zeigt der in Teilaufgabe (2) definierte Code $\mathcal{C}_{1}$? | + | {Welche Eigenschaften zeigt der in Teilaufgabe '''(2)''' definierte Code $\mathcal{C}_{1}$? |
|type="[]"} | |type="[]"} | ||
+ Ein Bitfehler lässt sich erkennen. | + Ein Bitfehler lässt sich erkennen. | ||
- Ein Bitfehler kann korrigiert werden. | - Ein Bitfehler kann korrigiert werden. | ||
| − | {Welche Eigenschaften zeigt der Code $\mathcal{C}_{4}= \{(0, 0, 0), (1, 1, 1)\}$? | + | {Welche Eigenschaften zeigt der Code $\mathcal{C}_{4}= \{(0, 0, 0), (1, 1, 1)\}$? |
|type="[]"} | |type="[]"} | ||
| − | - Die Coderate beträgt $R = 1/4$. | + | - Die Coderate beträgt $R = 1/4$. |
| − | + Die Coderate beträgt $R = 1/3$. | + | + Die Coderate beträgt $R = 1/3$. |
+ Ein Bitfehler lässt sich erkennen. | + Ein Bitfehler lässt sich erkennen. | ||
+ Ein Bitfehler kann korrigiert werden. | + Ein Bitfehler kann korrigiert werden. | ||
Version vom 2. Mai 2019, 16:19 Uhr
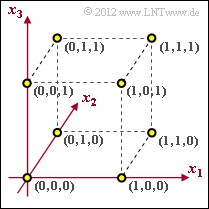
Codes zur Fehlererkennung bzw. Fehlererkorrektur lassen sich sehr anschaulich im $n$–dimensionalen Raum darstellen. Wir beschränken uns hier auf binäre Codes der Länge $n = 3$:
- $$\underline{x} = (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\hspace{0.5cm} x_i = \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$
Allgemein gilt bei der Blockcodierung:
- Das Informationswort $\underline{u} = (u_{1}, u_{2}, \ \text{...} , \ u_{k})$ wird eindeutig in das Codewort $\underline{x} =(x_{1}, x_{2}, \ \text{...} , \ , x_{n})$ überführt.
- Die Coderate beträgt $R = k/n$.
- Die Hamming–Distanz $d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')$ zwischen zwei Codeworten $x ∈ \mathcal{C}$ und $x\hspace{0.05cm}' ∈ \mathcal{C}$ gibt die Anzahl der Bitpositionen an, in denen sich $x$ und $x\hspace{0.05cm}'$ unterscheiden.
- Die Minimaldistanz $d_{\rm min} = {\rm min}\big[d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')\big]$ ist ein Maß für die Korrekturfähigkeit eines Codes.
- Es können $e =d_{\rm min} – 1$ Fehler erkannt und $t =(d_{\rm min} – 1)/2$ Fehler korrigiert werden.
- Die letzte Aussage gilt allerdings nur für ungerades $d_{\rm min}$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zielsetzung der Kanalcodierung.
- Zusätzlich werden einige einfache Fragen zum Kapitel Beispiele binärer Blockcodes vorweg genommen.
Fragebogen
Musterlösung
(1) Richtig sind die Aussagen 1 und 3:
- Bei dieser Belegung werden $k = 3$ Informationsbits auf $n = 3$ Codebits abgebildet ⇒ $R = k/n = 1$.
- Die Aussage $\underline{x} = \underline{u} $ würde nur bei systematischer Codierung gelten.
- Prinzipiell möglich wäre zum Beispiel auch $(0, 0, 0)$ → $(0, 1, 1)$.
- Die letzte Aussage ist mit Sicherheit falsch: Aus der Grafik erkennt man die Minimaldistanz $d_{\rm min} = 1$.
(2) Richtig sind die Aussagen 1 und 3:
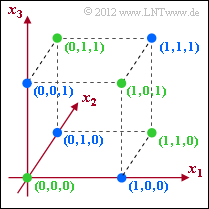
- $\mathcal{C}_{1}$ und $\mathcal{C}_{2}$ beschreiben tatsächlich Codes mit der Rate $R = 2/3$ und der Minimaldistanz $d_{\rm min} = 2$.
- In der Grafik markieren die grünen Punkte den Code $\mathcal{C}_{1}$ und die blauen Punkte den Code $\mathcal{C}_{2}$.
- Beim Code $\mathcal{C}_{3}$ – ebenfalls mit Rate $R = 2/3$ – ist die minimale Distanz zwischen zwei Codeworten $d_{\rm min} = 1$, zum Beispiel zwischen $(0, 0, 0)$ und $(1, 0, 0)$ oder zwischen $(0, 1, 1)$ und $(1, 1, 1)$.
(3) Richtig ist nur die Aussage 1:
- Mit der Minimaldistanz $d_{\rm min} = 2$ kann lediglich ein Bitfehler erkannt werden.
- In der oberen Grafik kennzeichnen die grünen Punkte zulässige Codeworte von $\mathcal{C}_{1}$. Wird ein blauer Punkt empfangen, so weist dies auf einen Übertragungsfehler hin.
- Eine Fehlerkorrektur ist mit $d_{\rm min} = 2$ dagegen nicht möglich.
- Der Code $\mathcal{C}_{1}$ entspricht dem Single Parity–check Code (3, 2, 2).
(4) Richtig sind die Antworten 2, 3 und 4:
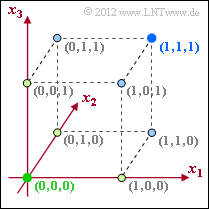
- $C_{4}$ beschreibt den (3, 1, 3)–Wiederholungscode.
- Bei diesem Code sind zwar zwei der insgesamt acht möglichen Punkte belegt, woraus man fälschlicherweise auf die Coderate $R = 1/4$ schließen könnte. Die Coderate berechnet sich aber gemäß $R = k/n = 1/3$.
- Aus der unteren Grafik erkennt man, dass wegen $d_{\rm min} = 3$ nun auch ein Bitfehler korrigiert werden kann.
- Bei der Decodierung werden alle hellgrünen Punkte (mit schwarzer Umrahmung) in den grünen Punkt $(0, 0, 0)$ überführt und alle hellblauen in den blauen Punkt $(1, 1, 1)$.
- Gleichzeitig können bis zu zwei Bitfehler erkannt werden (einer natürlich auch).