Aufgaben:Aufgabe 1.4: Zeigerdiagramm und Ortskurve: Unterschied zwischen den Versionen
K (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| Zeile 1: | Zeile 1: | ||
{{quiz-Header|Buchseite=Modulationsverfahren/Allgemeines_Modell_der_Modulation}} | {{quiz-Header|Buchseite=Modulationsverfahren/Allgemeines_Modell_der_Modulation}} | ||
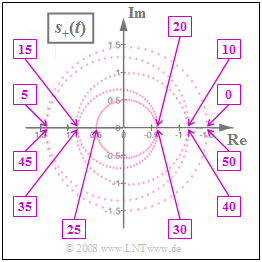
| − | [[Datei:P_ID966__Mod_A_1_4_neu.png|right|frame| | + | [[Datei:P_ID966__Mod_A_1_4_neu.png|right|frame|Vorgegebenes nalytisches Signal in der komplexen Ebene]] |
| − | Die beiliegende Grafik zeigt das analytische Signal $s_+(t)$ in der komplexen Ebene. Die in den Rechtecken angegebenen | + | Die beiliegende Grafik zeigt das analytische Signal $s_+(t)$ in der komplexen Ebene. |
| − | :$$s_+(t = 0) =s_+(t = 50\;{\rm | + | *Die in den Rechtecken angegebenen Zahlen geben die Zeitpunkte in Mikrosekunden an. |
| − | :$$s_+(t = 5\;{\rm | + | *Bei allen Vielfachen von $5 \ \rm µ s$ ist $s_+(t)$ stets reell und hat dabei folgende Werte: |
| − | :$$s_+(t = 10\;{\rm | + | :$$s_+(t = 0) =s_+(t = 50\;{\rm µ s})= 1.500\hspace{0.05cm},$$ |
| + | :$$s_+(t = 5\;{\rm µ s}) = s_+(t = 45\;{\rm µ s})= -1.405\hspace{0.05cm},$$ | ||
| + | :$$s_+(t = 10\;{\rm µ s}) = s_+(t = 40\;{\rm µ s})= 1.155\hspace{0.05cm},$$ | ||
:$$\text{.....................................} $$ | :$$\text{.....................................} $$ | ||
| − | :$$s_+(t = 25\;{\rm | + | :$$s_+(t = 25\;{\rm µ s}) = -0.500\hspace{0.05cm}.$$ |
| − | Als bekannt vorausgesetzt | + | Als bekannt vorausgesetzt wird, dass das dazugehörige physikalische Signal folgende Form hat: |
:$$s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T}\cdot t\right) + {A_0}/{2}\cdot \cos\left(\left(\omega_{\rm T} + \omega_{\rm 0}\right)\cdot t \right) + {A_0}/{2}\cdot \cos\left(\left(\omega_{\rm T} - \omega_{\rm 0}\right)\cdot t \right)\hspace{0.05cm}.$$ | :$$s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T}\cdot t\right) + {A_0}/{2}\cdot \cos\left(\left(\omega_{\rm T} + \omega_{\rm 0}\right)\cdot t \right) + {A_0}/{2}\cdot \cos\left(\left(\omega_{\rm T} - \omega_{\rm 0}\right)\cdot t \right)\hspace{0.05cm}.$$ | ||
| − | Gegeben ist | + | Gegeben ist die Frequenz des Trägersignals zu $f_{\rm T} = 100\text{ kHz}$. Ermittelt werden sollen die drei weiteren Parameter $f_0$, $A_{\rm T}$ und $A_0$. |
| − | Bezug genommen wird auch auf das [[Modulationsverfahren/Allgemeines_Modell_der_Modulation#Beschreibung_von_s.28t.29_mit_Hilfe_des_analytischen_Signals|äquivalente TP–Signal]] $s_{\rm TP}(t)$, wobei folgender Zusammenhang mit dem analytischen Signal besteht: | + | Bezug genommen wird auch auf das [[Modulationsverfahren/Allgemeines_Modell_der_Modulation#Beschreibung_von_s.28t.29_mit_Hilfe_des_analytischen_Signals|äquivalente TP–Signal]] $s_{\rm TP}(t)$, wobei folgender Zusammenhang mit dem analytischen Signal besteht: |
:$$s_{\rm TP}(t) = s_+(t) \cdot {\rm e}^{-{\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} \hspace{0.05cm}.$$ | :$$s_{\rm TP}(t) = s_+(t) \cdot {\rm e}^{-{\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Allgemeines_Modell_der_Modulation|Allgemeines Modell der Modulation]]. | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Allgemeines_Modell_der_Modulation|Allgemeines Modell der Modulation]]. |
| − | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Allgemeines_Modell_der_Modulation#Beschreibung_von_s.28t.29_mit_Hilfe_des_.C3.A4quivalenten_TP-Signals|Beschreibung von ''s''(''t'') mit Hilfe des äquivalenten_TP-Signals]]. | + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Allgemeines_Modell_der_Modulation#Beschreibung_von_s.28t.29_mit_Hilfe_des_.C3.A4quivalenten_TP-Signals|Beschreibung von ''s''(''t'') mit Hilfe des äquivalenten_TP-Signals]]. |
| − | *Weitere Informationen zu dieser Thematik finden Sie in den Kapiteln [[Signaldarstellung/Harmonische_Schwingung|Harmonische Schwingung]], [[Signaldarstellung/Analytisches_Signal_und_zugeh%C3%B6rige_Spektralfunktion|Analytisches Signal und zugehörige Spektralfunktion]] und [[Signaldarstellung/%C3%84quivalentes_Tiefpass-Signal_und_zugeh%C3%B6rige_Spektralfunktion| Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion]] | + | *Weitere Informationen zu dieser Thematik finden Sie in den Kapiteln des Buches „Signaldarstellung”: |
| + | ::(1) [[Signaldarstellung/Harmonische_Schwingung|Harmonische Schwingung]], | ||
| + | ::(2) [[Signaldarstellung/Analytisches_Signal_und_zugeh%C3%B6rige_Spektralfunktion|Analytisches Signal und zugehörige Spektralfunktion]] und | ||
| + | ::(3) [[Signaldarstellung/%C3%84quivalentes_Tiefpass-Signal_und_zugeh%C3%B6rige_Spektralfunktion| Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion]]. | ||
| − | *In unserem Tutorial LNTwww wird die Darstellung des analytischen Signals $s_+(t)$ in der komplexen Ebene teilweise auch als „Zeigerdiagramm” bezeichnet, während die „Ortskurve” den zeitlichen Verlauf des äquivalenten TP–Signals $s_{\rm TP}(t)$ angibt. Wir verweisen auf die entsprechenden | + | *In unserem Tutorial $\rm LNTwww$ wird die Darstellung des analytischen Signals $s_+(t)$ in der komplexen Ebene teilweise auch als „Zeigerdiagramm” bezeichnet, während die „Ortskurve” den zeitlichen Verlauf des äquivalenten TP–Signals $s_{\rm TP}(t)$ angibt. Wir verweisen auf die entsprechenden interaktiven Applets |
| + | ::(1) [[Applets:Physikalisches_Signal_%26_Analytisches_Signal|Physikalisches Signal & analytisches Signal ]], | ||
| + | ::(2) [[Applets:Physikalisches_Signal_%26_Äquivalentes_TP-Signal|Physikalisches Signal & äquivalentes TP-Signal]]. | ||
| Zeile 30: | Zeile 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie ausgehend von $s(t)$ die Gleichung für $s_+(t)$ an und vereinfachen Sie diese. Welche Gleichung gilt für das äquivalente Tiefpass–Signal? | + | {Geben Sie ausgehend von $s(t)$ die Gleichung für $s_+(t)$ an und vereinfachen Sie diese. <br>Welche Gleichung gilt für das äquivalente Tiefpass–Signal? |
|type="[]"} | |type="[]"} | ||
- Es gilt $s_{\rm TP}(t) = A_0 · {\rm e}^{–{\rm j}ω_0t}.$ | - Es gilt $s_{\rm TP}(t) = A_0 · {\rm e}^{–{\rm j}ω_0t}.$ | ||
| Zeile 36: | Zeile 45: | ||
+ Es gilt $s_{\rm TP}(t) = A_{\rm T} + A_0 · \cos(ω_0t).$ | + Es gilt $s_{\rm TP}(t) = A_{\rm T} + A_0 · \cos(ω_0t).$ | ||
| − | {Bestimmen Sie den Signalparameter $f_0$. | + | {Bestimmen Sie den Signalparameter $f_0$. |
|type="{}"} | |type="{}"} | ||
$f_0 \ = \ $ { 20 3% } $\ \text{kHz}$ | $f_0 \ = \ $ { 20 3% } $\ \text{kHz}$ | ||
| − | {Bestimmen Sie die weiteren Signalparameter $A_{\rm T}$ und $A_0$. | + | {Bestimmen Sie die weiteren Signalparameter $A_{\rm T}$ und $A_0$. |
|type="{}"} | |type="{}"} | ||
$A_{\rm T} \ = \ $ { 1 3% } | $A_{\rm T} \ = \ $ { 1 3% } | ||
| Zeile 46: | Zeile 55: | ||
| − | {Berechnen Sie die Werte des analytischen Signals $s_+(t)$ zu den Zeiten $t = 15$ | + | {Berechnen Sie die Werte des analytischen Signals $s_+(t)$ zu den Zeiten $t = 15 \;{\rm µ s}$ und $t = 20\;{\rm µ s}$. |
|type="{}"} | |type="{}"} | ||
$s_+(t = 15 \ \rm μs) \ = \ $ { -0.865--0.825 } | $s_+(t = 15 \ \rm μs) \ = \ $ { -0.865--0.825 } | ||
Version vom 4. Dezember 2018, 12:04 Uhr
Die beiliegende Grafik zeigt das analytische Signal $s_+(t)$ in der komplexen Ebene.
- Die in den Rechtecken angegebenen Zahlen geben die Zeitpunkte in Mikrosekunden an.
- Bei allen Vielfachen von $5 \ \rm µ s$ ist $s_+(t)$ stets reell und hat dabei folgende Werte:
- $$s_+(t = 0) =s_+(t = 50\;{\rm µ s})= 1.500\hspace{0.05cm},$$
- $$s_+(t = 5\;{\rm µ s}) = s_+(t = 45\;{\rm µ s})= -1.405\hspace{0.05cm},$$
- $$s_+(t = 10\;{\rm µ s}) = s_+(t = 40\;{\rm µ s})= 1.155\hspace{0.05cm},$$
- $$\text{.....................................} $$
- $$s_+(t = 25\;{\rm µ s}) = -0.500\hspace{0.05cm}.$$
Als bekannt vorausgesetzt wird, dass das dazugehörige physikalische Signal folgende Form hat:
- $$s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T}\cdot t\right) + {A_0}/{2}\cdot \cos\left(\left(\omega_{\rm T} + \omega_{\rm 0}\right)\cdot t \right) + {A_0}/{2}\cdot \cos\left(\left(\omega_{\rm T} - \omega_{\rm 0}\right)\cdot t \right)\hspace{0.05cm}.$$
Gegeben ist die Frequenz des Trägersignals zu $f_{\rm T} = 100\text{ kHz}$. Ermittelt werden sollen die drei weiteren Parameter $f_0$, $A_{\rm T}$ und $A_0$.
Bezug genommen wird auch auf das äquivalente TP–Signal $s_{\rm TP}(t)$, wobei folgender Zusammenhang mit dem analytischen Signal besteht:
- $$s_{\rm TP}(t) = s_+(t) \cdot {\rm e}^{-{\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Allgemeines Modell der Modulation.
- Bezug genommen wird insbesondere auf die Seite Beschreibung von s(t) mit Hilfe des äquivalenten_TP-Signals.
- Weitere Informationen zu dieser Thematik finden Sie in den Kapiteln des Buches „Signaldarstellung”:
- In unserem Tutorial $\rm LNTwww$ wird die Darstellung des analytischen Signals $s_+(t)$ in der komplexen Ebene teilweise auch als „Zeigerdiagramm” bezeichnet, während die „Ortskurve” den zeitlichen Verlauf des äquivalenten TP–Signals $s_{\rm TP}(t)$ angibt. Wir verweisen auf die entsprechenden interaktiven Applets
Fragebogen
Musterlösung
- $$s_+(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.03cm}t} + \frac{A_0}{2}\cdot {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}(\omega_{\rm T} + \omega_{\rm 0})\hspace{0.03cm}\cdot \hspace{0.05cm}t} + \frac{A_0}{2}\cdot {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}(\omega_{\rm T} - \omega_{\rm 0})\hspace{0.03cm}\cdot \hspace{0.03cm}t} = {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.03cm}t} \cdot \left[ A_{\rm T}+ \frac{A_0}{2} \cdot \left( {\rm e}^{\hspace{0.03cm}{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 0}\cdot \hspace{0.05cm}t} + {\rm e}^{\hspace{0.03cm}-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 0}\cdot \hspace{0.05cm}t}\right)\right]\hspace{0.05cm}.$$
Mit der Gleichung ${\rm e}^{{\rm j} · α} + {\rm e}^{-{\rm j} · α} = 2 · \cos(α)$ folgt weiter:
- $$s_+(t) = {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.03cm}t} \cdot \left[ A_{\rm T}+ {A_0} \cdot \cos (\omega_{\rm 0}\cdot t) \right] \hspace{0.05cm}.$$
Damit erhält man für das äquivalente Tiefpass–Signal:
- $$s_{\rm TP}(t) = s_+(t) \cdot {\rm e}^{-{\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} = A_{\rm T}+ {A_0} \cdot \cos (\omega_{\rm 0}\cdot t) \hspace{0.05cm}.$$
Richtig ist also derletzte Lösungsvorschlag. Im Kapitel „Hüllkurvendemodulation” des vorliegenden Buches werden wir sehen, dass es sich dabei um die Zweiseitenband–Amplitudenmodulation eines Cosinussignals mit cosinusförmigem Träger handelt.
(2) Die Periodendauer des analytischen Signals $s_+(t)$ beträgt $T_0 = 50$ μs. Das physikalische Signal $s(t)$ hat die gleiche Periodendauer.
Unter der Voraussetzung, dass $f_{\rm T}$ ein ganzzahliges Vielfaches von $f_0$ ist (was zu überprüfen ist, aber für dieses Beispiel zutrifft), ergibt sich $f_0 = 1/T_0 \hspace{0.15cm}\underline{ = 20 \ \rm kHz}$.
(3) Bei den gegebenen Zeitpunkten (Vielfache von $5$ μs) gilt für den komplexen Drehzeiger des Trägers:
- $${\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \cdot \hspace{0.05cm} {100\,{\rm kHz}}\cdot \hspace{0.05cm}(k \hspace{0.05cm}\cdot \hspace{0.05cm} 5\,{\rm \mu s})} = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}k \hspace{0.03cm} \cdot \hspace{0.05cm} \pi } = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right. \begin{array}{*{10}c} {\rm{falls}} \\ {\rm{falls}} \\ \end{array}\begin{array}{*{20}c} k \hspace{0.1cm}{\rm gerade} , \\ k \hspace{0.1cm}{\rm ungerade} . \\ \end{array}$$
Deshalb folgt aus der in der Teilaufgabe (1) berechneten Gleichung:
- $$k = 0 \Rightarrow \hspace{0.2cm} s_{\rm +}(t = 0) = A_{\rm T}+ {A_0} \cdot \cos (\omega_{\rm 0}\cdot 0) = A_{\rm T}+ {A_0} \hspace{0.05cm},$$
- $$k = 5 \Rightarrow \hspace{0.2cm} s_{\rm +}(t = 25\;{\rm \mu s}) = - \left[ A_{\rm T}+ {A_0} \cdot \cos (\omega_{\rm 0}\cdot {T_0}/{2}) \right] = -A_{\rm T}+ {A_0} \hspace{0.05cm}.$$
Ein Vergleich mit der ersten und letzten Gleichung auf dem Angabenblatt zeigt:
- $$ s_{\rm +}(t = 0) = A_{\rm T}+ {A_0}=1.5 \hspace{0.05cm}, $$
- $$ s_{\rm +}(t = 25\;{\rm \mu s}) = -A_{\rm T}+ {A_0} = -0.5 \hspace{0.05cm}.$$
Daraus erhält man $A_{\rm T} \hspace{0.15cm}\underline{ = 1}$ und $A_0 \hspace{0.15cm}\underline{ = 0.5}$.
(4) Zum Zeitpunkt $t = 15$ μs ($k = 3$, ungerade) gilt:
- $$ s_{\rm +}(t = 15\;{\rm \mu s}) = - \left[ 1+ 0.5 \cdot \cos (2 \pi \cdot 20\,{\rm kHz} \cdot 0.015\,{\rm ms}) \right] \hspace{0.05cm}, = -1- 0.5 \cdot \cos (108^{\circ})\hspace{0.15cm}\underline {= -0.845} \hspace{0.05cm}.$$
Dagegen ergibt sich für den Zeitpunkt $t = 20$ μs ($k = 4$, gerade):
- $$ s_{\rm +}(t = 20\;{\rm \mu s}) = 1 + 0.5 \cdot \cos (144^{\circ})\hspace{0.15cm}\underline {= 0.595} \hspace{0.05cm}.$$
Bei allen diesen betrachteten Zeitpunkten ist das physikalische Signal $s(t) = {\rm Re}[s_+(t)]$ genau so groß.