Aufgaben:Aufgabe 3.7: Winkelmodulation einer harmonischen Schwingung: Unterschied zwischen den Versionen
K (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| Zeile 5: | Zeile 5: | ||
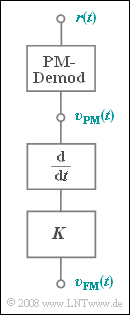
[[Datei:P_ID1103__Mod_Z_3_6.png|right|frame|Möglicher FM–Demodulator]] | [[Datei:P_ID1103__Mod_Z_3_6.png|right|frame|Möglicher FM–Demodulator]] | ||
Das an einem Empfänger ankommende Signal lautet: | Das an einem Empfänger ankommende Signal lautet: | ||
| − | :$$ r(t) = 3\,{\rm V} \cdot \cos\ | + | :$$ r(t) = 3\,{\rm V} \cdot \cos \hspace{-0.05cm} \big[2 \pi \cdot 1\,{\rm MHz} \cdot t + 3 \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\big]\hspace{0.05cm}.$$ |
| − | Bei $r(t)$ handelt es sich um ein winkelmoduliertes Signal, das bei der Übertragung weder verzerrt noch durch Rauschen beaufschlagt wurde. Die Signale $v_{\rm PM}(t)$ und $v_{\rm FM}(t)$ ergeben sich nach idealer Demodulation mittels | + | Bei $r(t)$ handelt es sich um ein winkelmoduliertes Signal, das bei der Übertragung weder verzerrt noch durch Rauschen beaufschlagt wurde. Die Signale $v_{\rm PM}(t)$ und $v_{\rm FM}(t)$ ergeben sich nach idealer Demodulation mittels |
* Phasendemodulator, gegeben durch die Gleichung | * Phasendemodulator, gegeben durch die Gleichung | ||
:$$ v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) \hspace{0.05cm},\hspace{0.3cm} {K_{\rm PM}} = 2\,{\rm V}^{-1}\hspace{0.05cm},$$ | :$$ v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) \hspace{0.05cm},\hspace{0.3cm} {K_{\rm PM}} = 2\,{\rm V}^{-1}\hspace{0.05cm},$$ | ||
| − | * Frequenzdemodulator, bestehend aus PM–Demodulator, Differenzierer und einer Konstanten $K$. Damit alle Signale gleiche Einheiten besitzen, ist diese Konstante $K$ dimensionsbehaftet. | + | * Frequenzdemodulator, bestehend aus PM–Demodulator, Differenzierer und einer Konstanten $K$. |
| + | |||
| + | |||
| + | Damit alle Signale gleiche Einheiten besitzen, ist diese Konstante $K$ dimensionsbehaftet. | ||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Frequenzmodulation_(FM)|Frequenzmodulation]]. | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Frequenzmodulation_(FM)|Frequenzmodulation]]. |
| − | *Bezug genommen wird aber auch auf das Kapitel [[Modulationsverfahren/Phasenmodulation_(PM)|Phasenmodulation]] und | + | *Bezug genommen wird aber auch auf das Kapitel [[Modulationsverfahren/Phasenmodulation_(PM)|Phasenmodulation]] und auf den Abschnitt [[Modulationsverfahren/Frequenzmodulation_(FM)#Signalverl.C3.A4ufe_bei_Frequenzmodulation|Signalverläufe bei Frequenzmodulation]]. |
| Zeile 26: | Zeile 32: | ||
+ Es könnte eine PM–Modulation vorliegen. | + Es könnte eine PM–Modulation vorliegen. | ||
+ Es könnte eine FM–Modulation vorliegen. | + Es könnte eine FM–Modulation vorliegen. | ||
| − | - Die Nachrichtenphase ist sicher $ϕ_{\rm N} = 0$. | + | - Die Nachrichtenphase ist sicher $ϕ_{\rm N} = 0$. |
| − | + Die Nachrichtenfrequenz ist sicher $f_{\rm N} = 10 \ \rm kHz$. | + | + Die Nachrichtenfrequenz ist sicher $f_{\rm N} = 10 \ \rm kHz$. |
| − | {Berechnen Sie das Signal $v_{\rm PM}(t)$ nach dem Phasendemodulator. Wie groß ist der Signalwert zum Zeitpunkt $t = 0$? | + | {Berechnen Sie das Signal $v_{\rm PM}(t)$ nach dem Phasendemodulator. Wie groß ist der Signalwert zum Zeitpunkt $t = 0$? |
|type="{}"} | |type="{}"} | ||
$v_{\rm PM}(t = 0) \ = \ $ { 1.5 3% } $\ \rm V$ | $v_{\rm PM}(t = 0) \ = \ $ { 1.5 3% } $\ \rm V$ | ||
| − | {Berechnen Sie das Signal $v_{\rm FM}(t)$. Wie groß ist die Nachrichtenphase $ϕ_{\rm N}$? | + | {Berechnen Sie das Signal $v_{\rm FM}(t)$. Wie groß ist die Nachrichtenphase $ϕ_{\rm N}$? |
|type="{}"} | |type="{}"} | ||
$ϕ_{\rm N} \ = \ $ { 90 3% } $\ \rm Grad$ | $ϕ_{\rm N} \ = \ $ { 90 3% } $\ \rm Grad$ | ||
| − | {Wie groß ist $K$ zu wählen, damit die Amplitude von $v_{\rm FM}(t)$ gleich $1.5 \ \rm V$ ist? | + | {Wie groß ist $K$ zu wählen, damit die Amplitude von $v_{\rm FM}(t)$ gleich $1.5 \ \rm V$ ist? |
|type="{}"} | |type="{}"} | ||
$K\ = \ $ { 6.28 3% } $\ \rm \cdot 10^4 \ 1/s$ | $K\ = \ $ { 6.28 3% } $\ \rm \cdot 10^4 \ 1/s$ | ||
| Zeile 44: | Zeile 50: | ||
{Welche der folgenden Aussagen treffen für das FM–modulierte Signal zu? | {Welche der folgenden Aussagen treffen für das FM–modulierte Signal zu? | ||
|type="[]"} | |type="[]"} | ||
| − | + Der Phasenhub beträgt $ϕ_{\rm max} = 3$. | + | + Der Phasenhub beträgt $ϕ_{\rm max} = 3$. |
| − | + Der Frequenzhub beträgt $Δf_{\rm A} = 30 \ \rm kHz$. | + | + Der Frequenzhub beträgt $Δf_{\rm A} = 30 \ \rm kHz$. |
| − | + Es treten Augenblicksfrequenzen zwischen $0.97\ \rm MHz$ und $1.03 \ \rm MHz$ auf. | + | + Es treten Augenblicksfrequenzen zwischen $0.97\ \rm MHz$ und $1.03 \ \rm MHz$ auf. |
| − | - Mit $f_{\rm N} = 5 \ \rm kHz$ würde sich am Phasenhub nichts ändern. | + | - Mit $f_{\rm N} = 5 \ \rm kHz$ würde sich am Phasenhub nichts ändern. |
| − | + Mit $f_{\rm N} = 5 \ \rm kHz$ würde sich am Frequenzhub nichts ändern. | + | + Mit $f_{\rm N} = 5 \ \rm kHz$ würde sich am Frequenzhub nichts ändern. |
</quiz> | </quiz> | ||
Version vom 20. Dezember 2018, 13:53 Uhr
Das an einem Empfänger ankommende Signal lautet:
- $$ r(t) = 3\,{\rm V} \cdot \cos \hspace{-0.05cm} \big[2 \pi \cdot 1\,{\rm MHz} \cdot t + 3 \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\big]\hspace{0.05cm}.$$
Bei $r(t)$ handelt es sich um ein winkelmoduliertes Signal, das bei der Übertragung weder verzerrt noch durch Rauschen beaufschlagt wurde. Die Signale $v_{\rm PM}(t)$ und $v_{\rm FM}(t)$ ergeben sich nach idealer Demodulation mittels
- Phasendemodulator, gegeben durch die Gleichung
- $$ v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) \hspace{0.05cm},\hspace{0.3cm} {K_{\rm PM}} = 2\,{\rm V}^{-1}\hspace{0.05cm},$$
- Frequenzdemodulator, bestehend aus PM–Demodulator, Differenzierer und einer Konstanten $K$.
Damit alle Signale gleiche Einheiten besitzen, ist diese Konstante $K$ dimensionsbehaftet.
Hinweise:
- Die Aufgabe gehört zum Kapitel Frequenzmodulation.
- Bezug genommen wird aber auch auf das Kapitel Phasenmodulation und auf den Abschnitt Signalverläufe bei Frequenzmodulation.
Fragebogen
Musterlösung
- Aus der Gleichung für $r(t)$ kann lediglich abgelesen werden, dass es sich um eine Winkelmodulation handelt, nicht jedoch, ob eine Phasenmodulation (PM) oder eine Frequenzmodulation (FM) vorliegt.
- Aufgrund der Gleichung steht fest, dass die Nachrichtenfrequenz $f_{\rm N} = 10 \ \rm kHz$ beträgt.
- Die Phase $ϕ_{\rm N} = 0$ des Quellensignals würde dagegen nur zutreffen, wenn eine Phasenmodulation vorläge.
(2) Mit der Modulatorkonstanten $K_{\rm PM} = 2 \ \rm V^{–1}$ erhält man hierfür:
- $$v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) = \frac{3}{2\,{\rm V}^{-1}} \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$
Für den Zeitpunkt $t = 0$ gilt deshalb:
- $$v_{\rm PM}(t = 0) = {A_{\rm N}} \hspace{0.15cm}\underline {= 1.5\,{\rm V}}\hspace{0.05cm}.$$
(3) Für das Ausgangssignal $v_{\rm FM}(t)$ des FM–Demodulators – bestehend aus PM–Demodulator und Differenzierer – kann man schreiben:
- $$v_{\rm FM}(t) = \frac{{\rm d}v_{\rm PM}(t)}{{\rm d}t} \cdot K = \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot (- \sin(2 \pi \cdot {f_{\rm N}} \cdot t))= \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot \cos(2 \pi \cdot {f_{\rm N}} \cdot t + 90^\circ)\hspace{0.05cm}.$$
Die Nachrichtenphase ist somit $ϕ_{\rm N} \hspace{0.15cm}\underline {= 90^\circ}$.
(4) In diesem Fall muss gelten: $ K ={2 \pi \cdot f_{\rm N}} \hspace{0.15cm}\underline { = 6.28 \cdot 10^{4} \,\,{1}/{ s}} \hspace{0.05cm}.$
(5) Richtig sind die Lösungsvorschläge 1, 2, 3 und 5:
- Der Phasenhub ist identisch mit dem Modulationsindex, der aus der angegebenen Gleichung abgelesen werden kann:
- $$\phi_{\rm max} = \eta = 3 = \frac{\Delta f_{\rm A}}{ f_{\rm N}} \hspace{0.05cm}.$$
- Damit erhält man den Frequenzhub $Δf_{\rm A} = 3 · f_{\rm N} = 30 \ \rm kHz$.
- Mit der Trägerfrequenz $f_{\rm T} = 1 \ \rm MHz$ kann somit die Augenblicksfrequenz $f_{\rm T}(t)$ nur Werte zwischen $1±0.03 MHz$ annehmen.
Es gilt also auch folgende Aussage:
Bei halber Nachrichtenfrequenz verdoppelt sich der Phasenhub $η$, während der Frequenzhub $Δf_{\rm A}$ davon nicht beeinflusst wird:
- $$\eta = \frac{K_{\rm PM} \cdot A_{\rm N}}{ f_{\rm N}} = 6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} = \eta \cdot f_{\rm N} = 6 \cdot 5\,{\rm kHz} = 30\,{\rm kHz}\hspace{0.05cm}.$$