Aufgaben:Aufgabe 2.4Z: Tiefpass-Einfluss bei Synchrondemodulation

• Zurück zum Buch

Signale bei ZSB–AM und Synchrondemodulation

Wir betrachten das gleiche Übertragungssystem wie in  Aufgabe 2.4. Es wird nun allerdings stets eine perfekte Frequenz– und Phasensynchronisation des Synchrondemodulators $\rm (SD)$ vorausgesetzt.

Das Quellensignal  $q(t)$, das Sendesignal  $s(t)$  sowie das Signal  $b(t)$  vor dem Tiefpassfilter innerhalb des Synchrondemodulators sind wie folgt gegeben:

$$q(t) = q_1(t) + q_2(t)\hspace{0.2cm}{\rm mit }$$

$$q_1(t) = 2\,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

$$q_2(t) = 1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

$$s(t) = q(t) \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

$$b(t) = s(t) \cdot 2 \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$

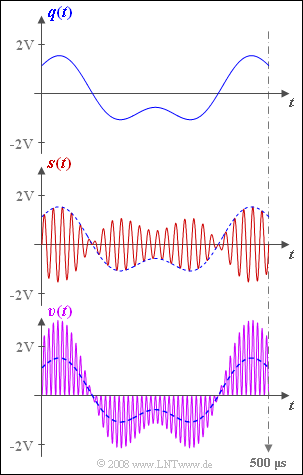
Die Grafik zeigt oben das Quellensignal  $q(t)$  und in der Mitte das Sendesignal  $s(t)$.

In der letzten Skizze ist das Sinkensignal  $v(t)$  dargestellt (violetter Kurvenverlauf).

• Dieses stimmt offensichtlich nicht mit dem Quellensignal (blau-gestrichelte Kurve) überein.
• Der Grund für das unerwünschte Ergebnis  $v(t) ≠ q(t)$  könnte zum Beispiel ein fehlender oder falsch dimensionierter Tiefpass sein.

In den Teilaufgaben (3) und (4) wird der so genannte  Trapeztiefpass  verwendet, dessen Frequenzgang wie folgt lautet:

$$H_{\rm E}(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 -|f|}{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_1,} \\ {f_1 \le \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\hspace{0.94cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > f_2.} \\ \end{array}$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Synchrondemodulation.
• Bezug genommen wird insbesondere auf die Seite  Blockschaltbild und Zeitbereichsdarstellung.
• Im Gegensatz zur  Aufgabe 2.4  beschreiben hier  $f_1$  und  $f_2$  nicht Signalfrequenzen, sondern beziehen sich auf das Tiefpassfilter.

Fragebogen

1

Welche Aussagen sind über das Filter  $H_{\rm E}(f)$  möglich, das zur Gewinnung des auf der Angabenseite dargestellten Sinkensignals benutzt wurde?

	Die obere Grenzfrequenz ist zu hoch.
	Die obere Grenzfrequenz ist zu niedrig.
	Die untere Grenzfrequenz ist ungleich Null.

2

Mit welchen der nachfolgend aufgeführten Tiefpassfunktionen ist eine ideale Demodulation – das heißt $v(t) = q(t)$ – prinzipiell möglich?

	Rechtecktiefpass,
	Gaußtiefpass,
	Trapeztiefpass,
	Spalttiefpass.

3

Wie ist die untere Eckfrequenz  $f_1$  eines Trapeztiefpasses mindestens zu wählen, damit keine Verzerrungen entstehen?

$f_{\text{1, min}} \ = \ $ $\ \text{kHz}$

4

Wie groß darf die obere Eckfrequenz  $f_2$  des Trapeztiefpasses höchstens sein, damit keine Verzerrungen entstehen?

$f_{\text{2, max}} \ = \ $ $\ \text{kHz}$

5

Welche Grenzfrequenz  $f_{\rm G}$  eines idealen, rechteckförmigen Tiefpasses würden Sie wählen, wenn Rauschstörungen nicht zu vernachlässigen sind?

	$f_{\rm G} = 4 \ \rm kHz$,
	$f_{\rm G} = 6 \ \rm kHz$,
	$f_{\rm G} = 10 \ \rm kHz$.

Musterlösung

Musterlösung

(1)  Richtig ist die erste Aussage:

• Das dargestellte Sinkensignal $v(t)$ stimmt exakt mit dem als Gleichung gegebenen Signal $b(t)$ überein und enthält somit auch Anteile um die doppelte Trägerfrequenz.
• Das Filter $H_{\rm E}(f)$ fehlt entweder ganz oder dessen obere Grenzfrequenz $f_2$ ist zu hoch.
• Bezüglich der unteren Grenzfrequenz $f_1$ ist nur die Aussage möglich, dass diese kleiner ist als die kleinste im Signal $b(t)$ vorkommende Frequenz (2 kHz).
• Ob ein Gleichanteil durch das Filter entfernt wird oder nicht, ist unklar, da ein solcher im Signal $b(t)$ nicht enthalten ist.

(2)  Richtig sind die Aussagen 1 und 3:

• Voraussetzung für eine verzerrungsfreie Demodulation ist, dass bis zu einer bestimmten Frequenz $f_1$ alle Spektralanteile gleich und möglichst ungedämpft übertragen werden und alle Anteile bei Frequenzen $f > f_2$ vollständig unterdrückt werden.
• Der Rechteck– und der Trapeztiefpass erfüllen diese Bedingung.

(3)  Sichergestellt werden muss, dass der 5 kHz–Anteil noch im Durchlassbereich liegt: $f_{\text{1, min}}\hspace{0.15cm}\underline{ =5 \ \rm kHz}$.

(4)  Alle Spektralanteile in der Umgebung der doppelten Trägerfrequenz – genauer gesagt zwischen 95 kHz und 105 kHz – müssen vollständig unterdrückt werden: $f_{\text{2, max}}\hspace{0.15cm}\underline{ =95 \ \rm kHz}$. Ansonsten würde es zu nichtlinearen Verzerrungen kommen.

(5)  Richtig ist der Lösungsvorschlag 2:

• Die Grenzfrequenz $f_{\rm G} = 4$ kHz hätte (lineare) Verzerrungen zur Folge, da dann der 5 kHz–Anteil abgeschnitten würde.
• Zu bevorzugen ist der Tiefpass mit der Grenzfrequenz $f_{\rm G} = 6$ kHz, da mit $f_{\rm G} = 10$ kHz dem Nutzsignal $v(t)$ mehr Rauschanteile überlagert wären.