Applets:Entropie und Näherungen binärer Nachrichtenquellen: Unterschied zwischen den Versionen
| Zeile 206: | Zeile 206: | ||
| − | + | == Zusammenfassung und Schlussfolgerungen == | |
| + | <br> | ||
| + | === Unbekannte Binärquelle === | ||
| + | * Ist von der Nachrichtenquelle nicht mehr bekannt als der Symbolunfang $M=2$, so müssen die Entropienäherungen $H_k$ numerisch aus der Quellensymbolfolge $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν–1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} ,\hspace{0.05cm}\text{ ...}\hspace{0.05cm},\hspace{0.05cm}q_{N} \hspace{0.05cm}〉$ ermittelt werden. Die Entropie $H$ ergibt sich als der Grenzwert der $H_k$ für $k \to \infty$, wobei gilt: | ||
| + | :$$ H <\text{...} < H_k <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.05cm}.$$ | ||
| + | * Bei der numerischen Ermittlung werden alle Wahrscheinlichkeiten $(p_{\rm A}, \text{...})$ und bedingten Wahrscheinlichkeiten $(p_{\rm A|B}, \text{...})$ durch entsprechende relative Häufigkeiten $(h_{\rm A}, \text{...})$ und bedingten Wahrscheinlichkeiten $(h_{\rm A|B}, \text{...})$ angenähert. | ||
| + | * Die Genauigkeit der numerischen Ermittlung nimmt bei gleichem $N$ mit steigendem $k$ ab. Das heißt: Die Folgenlänge $N$ der Simulation muss den den größten $k$–Wert angepasst werden. | ||
| + | |||
| + | |||
| + | === Gedächtnislose Binärquelle === | ||
| + | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Fazit:}$ | $\text{Fazit:}$ | ||
Version vom 8. Dezember 2018, 17:57 Uhr
Inhaltsverzeichnis
Programmbeschreibung
Dieses Applet soll den Begriff „Entropie” am Beispiel einer binären Nachrichtenquelle verdeutlichen. Die Quellensymbolfolge lautet somit $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν–1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} ,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}〉$ mit $q_i \in \{A, B\}$ für $i \ge 1$. Betrachtet werden sowohl eine gedächtnisfreie Quelle als auch eine Markovquelle erster Ordnung (also mit Gedächtnis „1”), deren Entropien $H$ jeweils in geschlossener Form angegeben werden können. Implizit vorausgesetzt ist hierbei die Folgenlänge $N \to \infty$.
Die Entropie $H$ lässt sich aber auch aus einer begrenzten Quellensymbolfolge $〈 q_1 \hspace{0.05cm}〉 =〈 q_1 , \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{N}\hspace{0.05cm}〉$ annähern, also auch dann, wenn die statistischen Eigenschaften der Binärquelle unbekannt sind. Auch hierauf wird in der folgenden Beschreibung eingegangen mit dem Fazit:
- Die Näherung ist natürlich um so genauer, je größer $N$ ist.
- Ist über die Quelle nichts weiter bekannt als die beispielhafte Folge, so ist der Rechenaufwand enorm.
Theoretischer Hintergrund
Die Entropie spielt in vielen naturwissenschaftlichen Fachgebieten eine große Rolle. Beschränken wir uns auf unser Fachgebiet der Statistik und der Informationstechnik, so ist die Entropie nach der Definition von Claude E. Shannon unter anderem ein Maß für die mittlere Unsicherheit über den Ausgang eines statistischen Ereignisses, für die „Zufälligkeit” dieses Ereignisses und für den mittleren Informationsgehalt einer Zufallsgröße.
Entropie einer gedächtnislosen Binärquelle
Wir setzen zunächst voraus, dass die Auftrittwahrscheinlichkeiten der beiden Symbole $\rm A$ und $\rm B$ unabhängig von den vorherigen Symbolen innerhalb der Folg gleich $p_{\rm A} = p$ und $p_{\rm B} = 1 – p$ seien.
Für die Entropie dieser „gedächtnislosen” Binärquelle gilt:
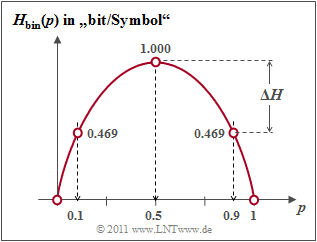
- $$H = H_{\rm bin} (p) = p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1-p} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
Man bezeichnet die Funktion $H_\text{bin}(p)$ als die binäre Entropiefunktion. Aus der Grafik erkennt man:
- Der Maximalwert $H_\text{0} = 1\; \rm bit$ ergibt sich für $p = 0.5$, also für gleichwahrscheinliche Binärsymbole. Dann liefern $\rm A$ und $\rm B$ jeweils den gleichen Beitrag zur Entropie. $H_\text{0}$ nennt man auch den Informationsgehalt.
- $H_\text{bin}(p)$ ist symmetrisch um $p = 0.5$. Eine Quelle mit $p_{\rm A} = 0.1$ und $p_{\rm B} = 0.9$ hat die gleiche Entropie $H = 0.469 \; \rm bit$ wie eine Quelle mit $p_{\rm A} = 0.9$ und $p_{\rm B} = 0.1$.
- Die Differenz $ΔH = H_\text{0} - H$ gibt die Redundanz der Quelle an und $r = ΔH/H_\text{0}$ die relative Redundanz. Im Beispiel ergeben sich $ΔH = 0.531\; \rm bit$ bzw. $r = 53.1 \rm \%$.
- Für $p = 0$ ergibt sich $H = 0$, da hier die Symbolfolge $\rm B \ B \ B \text{...}$ mit Sicherheit vorhergesagt werden kann. Eigentlich ist nun der Symbolumfang nur noch $M = 1$. Gleiches gilt für $p = 1$, also für die Symbolfolge $\rm A A A \text{...}$
Entropie hinsichtlich Zweiertupel
Wir teilen nun die Quellensymbolfolge $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν–1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} ,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}〉$ in Zweiertupel auf (siehe Grafik) auf und betrachten dadurch die Entropie zweier aufeinanderfolgender Quellensymbole.
Die Binärquelle wird weiterhin wie im letzten Abschnitt als gedächtnislos bzw. redundanzfrei vorausgesetzt. Für die Kombination $(q_ν, \hspace{0.05cm}q_{ν+1})$ gibt es in diesem Fall $2^2 = 4$ mögliche Symbolpaare (farblich markiert) mit folgenden Verbundwahrscheinlichkeiten:
- $${\rm Pr}(q_{\nu}\cap q_{\nu+1})\le {\rm Pr}(q_{\nu}) \cdot {\rm Pr}( q_{\nu+1}) \hspace{0.05cm}.$$
Daraus ist die Verbundentropie eines Zweier–Tupels berechenbar (der Index „2” symbolisiert, dass sich die so berechnete Entropie auf Zweiertupel bezieht):
- $$H_2\hspace{0.05cm}' = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} \sum_{q_{\nu+1}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm} q_{\mu}\hspace{0.01cm} \}}\hspace{-0.1cm}{\rm Pr}(q_{\nu}\cap q_{\nu+1}) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu}\cap q_{\nu+1})} \hspace{0.4cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Zweiertupel}) \hspace{0.05cm}.$$
Um den mittleren Informationsgehalt pro Symbol zu erhalten, muss $H_2\hspace{0.05cm}'$ noch halbiert werden:
- $$H_2 = {H_2\hspace{0.05cm}'}/{2} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol}) \hspace{0.05cm}.$$
Um eine konsistente Nomenklatur zu erreichen, benennen wir nun die im letzten Abschnitt definierte Entropie mit $H_1$:
- $$H_1 = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} {\rm Pr}(q_{\nu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu})} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol}) \hspace{0.05cm}.$$
Der Index „1” soll darauf hinweisen, dass $H_1$ ausschließlich die Symbolwahrscheinlichkeiten berücksichtigt und nicht statistischen Bindungen zwischen Symbolen innerhalb der Folge. Mit dem Entscheidungsgehalt $H_0 = \log_2 2 = 1\text{ (bit)}$ ergibt sich dann folgende Größenbeziehung:
- $$H_0 \ge H_1 \ge H_2 \hspace{0.05cm}.$$
Verdeutlichen wir uns nun die Berechnung der Entropienäherungen $H_1$ und $H_2$ an zwei Beispielen.
$\text{Beispiel 1:}$ Wir betrachten zunächst eine gedächtnislose Binärquelle mit gleichwahrscheinlichen Symbolen, das heißt es gelte $p_{\rm A} = p_{\rm B} = 1/2$. Die ersten zwanzig Folgenelemente lauten: $〈 q_ν 〉 =\rm BBAAABAABBBBBAAAABAB$ ...
- Aufgrund der gleichwahrscheinlichen Binärsymbole ist $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/Symbol$.
- Die Verbundwahrscheinlichkeit $p_{\rm AB}$ der Kombination $\rm AB$ ist gleich $p_{\rm A} · p_{\rm B} = 1/4$. Ebenso gilt $p_{\rm AA} = p_{\rm BB} = p_{\rm BA} = 1/4$.
- Damit erhält man für die zweite Entropienäherung
- $$H_2 = {1}/{2} \cdot \big [ {1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 + {1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 +{1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 +{1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 \big ] = 1 \,{\rm bit/Symbol} = H_1 = H_0 \hspace{0.05cm}.$$
$\text{Beispiel 2:}$ Die zweite hier betrachtete Folge ergibt sich aus der Folge von $\text{Beispiel 1}$ durch Anwendung eines einfachen Wiederholungscodes:
- $$〈 q_ν 〉 =\rm BbBbAaAaAaBbAaAaBbBb \text{...} $$
- Die wiederholten Symbole sind durch entsprechende Kleinbuchstaben dargestellt. Es handelt sich trotzdem um eine Binärquelle.
- Aufgrund der gleichwahrscheinlichen Binärsymbole ergibt sich auch hier $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/Symbol$.
- Für die Verbundwahrscheinlichkeiten gilt nun $p_{\rm AA}=p_{\rm BB} = 3/8$ und $p_{\rm ABA}=p_{\rm BAB} = 1/8$. Daraus folgt:
- $$\begin{align*}H_2 ={1}/{2} \cdot \big [ 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm} {8}/{3} + 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8\big ] = {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 - {3}/{8} \cdot{\rm log}_2\hspace{0.1cm}3 + {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 \approx 0.906 \,{\rm bit/Symbol} < H_1 = H_0 \hspace{0.05cm}.\end{align*}$$
Betrachtet man sich die Aufgabenstellung genauer, so kommt man zu folgendem Schluss:
- Die Entropie müsste eigentlich $H = 0.5 \hspace{0.05cm} \rm bit/Symbol$ sein (jedes zweite Symbol liefert keine neue Information).
- Die zweite Entropienäherung $H_2 = 0.906 \hspace{0.05cm} \rm bit/Symbol$ ist aber deutlich größer als die Entropie $H$.
- Zur Entropiebestimmung dieser redundanten Symbolfolge reicht die Näherung zweiter Ordnung nicht aus.
- Vielmehr muss man größere zusammenhängende Blöcke mit $k > 2$ Symbolen betrachten. Einen solchen Block bezeichnen wir im Folgenden als $k$–Tupel.
Verallgemeinerung auf $k$–Tupel und Grenzübergang
Wir schreiben zur Abkürzung mit der Verbundwahrscheinlichkeit $p_i^{(k)}$ eines $k$–Tupels allgemein:
- $$H_k = \frac{1}{k} \cdot \sum_{i=1}^{M^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{p_i^{(k)}} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol}) \hspace{0.05cm}.$$
- Die Laufvariable $i$ steht jeweils für eines der $M^k$ Tupel. Bei den hier betrachteten Binärquellen gilt $M=2$.
- Die vorher berechnete Näherung $H_2$ ergibt sich mit $k = 2$.
- Für die Entropienäherungen $H_k$ gelten folgende Größenrelationen; $H_0 = 1\text{ (bit/Symbol)}$ ist wieder der Entscheidungsgehalt:
- $$H \le \text{...} \le H_k \le \text{...} \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$
- Die Entropie einer Nachrichtenquelle mit Gedächtnis ist der folgende Grenzwert:
- $$H = \lim_{k \rightarrow \infty }H_k \hspace{0.05cm}.$$
Der Rechenaufwand wird bis auf wenige Sonderfälle $($siehe nachfolgendes $\text{Beispiel 3)}$ mit zunehmendem $k$ immer größer:
- Zur Berechnung von $H_{10}$ einer Binärquelle ist über $2^{10} = 1024$ Terme zu mitteln.
- Mit jeder weiteren Erhöhung von $k$ um $1$ verdoppelt sich die Anzahl der Summenterme.
$\text{Beispiel 3:}$ Wir betrachten eine alternierende Binärfolge ⇒ $〈 q_ν 〉 =\rm ABABABAB$ ... . Entsprechend gilt $H_0 = H_1 = 1 \hspace{0.15cm} \rm bit/Symbol$.
In diesem Sonderfall muss zur Bestimmung der $H_k$–Näherung unabhängig von $k$ stets nur über zwei Verbundwahrscheinlichkeiten gemittelt werden:
- $k = 2$: $p_{\rm AB} = p_{\rm BA} = 1/2$ ⇒ $H_2 = 1/2 \hspace{0.15cm} \rm bit/Symbol$,
- $k = 3$: $p_{\rm ABA} = p_{\rm BAB} = 1/2$ ⇒ $H_3 = 1/3 \hspace{0.15cm} \rm bit/Symbol$,
- $k = 4$: $p_{\rm ABAB} = p_{\rm BABA} = 1/2$ ⇒ $H_4 = 1/4 \hspace{0.15cm} \rm bit/Symbol$.
Die (tatsächliche) Entropie dieser alternierenden Binärfolge ist demzufolge
- $$H = \lim_{k \rightarrow \infty }{1}/{k} = 0 \hspace{0.05cm}.$$
Dieses Ergebnis war zu erwarten, da die betrachtete Folge nur minimale Information besitzt, die sich allerdings im Entropie–Endwert $H$ nicht auswirkt, nämlich die Information: „Tritt $\rm A$ zu den geraden oder ungeraden Zeitpunkten auf?”
Man erkennt, dass $H_k$ dem Endwert $H = 0$ nur sehr langsam näher kommt: Die zwanzigste Entropienäherung liefert immer noch $H_{20} = 0.05 \hspace{0.15cm} \rm bit/Symbol$.
Binärquellen mit Markoveigenschaften
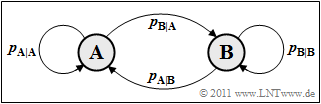
Folgen mit statistischen Bindungen zwischen den Folgenelementen (Symbolen) werden oft durch Markovprozesse modelliert, wobei wir uns hier auf binäre Markovprozesse erster Ordnung mit den Zuständen (Symbolen) $\rm A$ und $\rm B$ beschränken.
Rechts sehen Sie das Übergangsdiagramm für einen binären Markovprozess erster Ordnung. Von den vier angegebenen Übertragungswahrscheinlichkeiten sind allerdings nur zwei frei wählbar, zum Beispiel
- $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = \rm Pr(A\hspace{0.01cm}|\hspace{0.01cm}B)$ ⇒ bedingte Wahrscheinlichkeit, dass $\rm A$ auf $\rm B$ folgt.
- $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} = \rm Pr(B\hspace{0.01cm}|\hspace{0.01cm}A)$ ⇒ bedingte Wahrscheinlichkeit, dass $\rm B$ auf $\rm A$ folgt.
Für die beiden weiteren Übergangswahrscheinlichkeiten gilt dann $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1- p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$ und $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} = 1- p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}
\hspace{0.05cm}.$
Aufgrund der vorausgesetzten Eigenschaften Stationarität und Ergodizität gilt für die Zustands– bzw. Symbolwahrscheinlichkeiten:
- $$p_{\rm A} = {\rm Pr}({\rm A}) = \frac{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B} = {\rm Pr}({\rm B}) = \frac{p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$
Diese Gleichungen erlauben erste informationstheoretische Aussagen über Markovprozesse:
- Für $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$ sind die Symbole gleichwahrscheinlich ⇒ $p_{\text{A}} = p_{\text{B}}= 0.5$. Die erste Entropienäherung liefert demzufolge $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/Symbol$, und zwar unabhängig von den tatsächlichen Werten der (bedingten) Übergangswahrscheinlichkeiten $p_{\text{A|B}}$ bzw. $p_{\text{B|A}}$.
- Die Quellenentropie $H$ als der Grenzwert $($für $k \to \infty)$ der Entropienäherung $k$–ter Ordnung ⇒ $H_k$ hängt aber sehr wohl von den tatsächlichen Werten von $p_{\text{A|B}}$ und $p_{\text{B|A}}$ ab und nicht nur von ihrem Quotienten. Dies zeigt das folgende Beispiel.
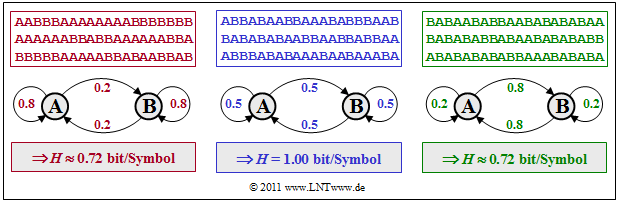
$\text{Beispiel 4:}$ Wir betrachten drei Markovquellen, die sich durch die Zahlenwerte der symmetrischen Übergangswahrscheinlichkeiten $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} }$ unterscheiden.
- Für die Symbolwahrscheinlichkeiten gilt somit $p_{\rm A} = p_{\rm B}= 0.5$.
- Die anderen Übergangswahrscheinlichkeiten haben dann die Werte $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 1 - p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}B} }.$
- Die mittlere (blaue) Symbolfolge mit $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.5$ besitzt die Entropie $H ≈ 1 \hspace{0.05cm} \rm bit/Symbol$. Das heißt: In diesem Sonderfall gibt es keine statistischen Bindungen innerhalb der Folge.
- Die linke (rote) Folge mit $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.25$ weist weniger Wechsel zwischen $\rm A$ und $\rm B$ auf. Aufgrund von statistischen Abhängigkeiten zwischen benachbarten Symbolen ist nun $H ≈ 0.72 \hspace{0.05cm} \rm bit/Symbol$ kleiner.
- Die rechte (grüne) Symbolfolge mit $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.8$ hat die genau gleiche Entropie $H ≈ 0.72 \hspace{0.05cm} \rm bit/Symbol$ wie die rote Folge. Hier erkennt man viele Bereiche mit sich stets abwechselnden Symbolen (... $\rm ABABAB$ ... ).
Für den allgemeineren Fall $p_{\text{A}} \ne p_{\text{B}}$ ist die Entropieberechnung der Zweiertupel etwas komplizierter:
- Mit den Verbundwahrscheinlichkeiten, zum Beispiel $p_{\text{AB}} = p_{\text{A}} · p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, kann geschrieben werden:
- $$H_2\hspace{0.05cm}' = p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
- Ersetzt man nun die Logarithmen der Produkte durch entsprechende Summen von Logarithmen, so erhält man das Ergebnis $H_2\hspace{0.05cm}' = H_1 + H_{\text{M}}$ mit
- $$H_1 = p_{\rm A} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} = H_{\rm bin} (p_{\rm A})= H_{\rm bin} (p_{\rm B}) \hspace{0.05cm},$$
- $$H_{\rm M}= p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
- Damit lautet die zweite Entropienäherung (mit der Einheit „bit/Symbol”):
- $$H_2 = {1}/{2} \cdot {H_2\hspace{0.05cm}'} = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big] \hspace{0.05cm}.$$
- Erweitert man dieses Ergebnis für $H_2$ auf die $k$–te Entropienäherung, so erhält man:
- $$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ].$$
- Die Entropie einer Markovquelle ergibt sich als der folgende Grenzwert und ist demzufolge einfach zu berechnen:
- $$H = \lim_{k \rightarrow \infty }H_k \hspace{0.5cm}\Rightarrow \hspace{0.5cm} H = H_{\rm M} = 2 \cdot H_2 - H_1 \hspace{0.05cm}.$$
Zusammenfassung und Schlussfolgerungen
Unbekannte Binärquelle
- Ist von der Nachrichtenquelle nicht mehr bekannt als der Symbolunfang $M=2$, so müssen die Entropienäherungen $H_k$ numerisch aus der Quellensymbolfolge $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν–1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} ,\hspace{0.05cm}\text{ ...}\hspace{0.05cm},\hspace{0.05cm}q_{N} \hspace{0.05cm}〉$ ermittelt werden. Die Entropie $H$ ergibt sich als der Grenzwert der $H_k$ für $k \to \infty$, wobei gilt:
- $$ H <\text{...} < H_k <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.05cm}.$$
- Bei der numerischen Ermittlung werden alle Wahrscheinlichkeiten $(p_{\rm A}, \text{...})$ und bedingten Wahrscheinlichkeiten $(p_{\rm A|B}, \text{...})$ durch entsprechende relative Häufigkeiten $(h_{\rm A}, \text{...})$ und bedingten Wahrscheinlichkeiten $(h_{\rm A|B}, \text{...})$ angenähert.
- Die Genauigkeit der numerischen Ermittlung nimmt bei gleichem $N$ mit steigendem $k$ ab. Das heißt: Die Folgenlänge $N$ der Simulation muss den den größten $k$–Wert angepasst werden.
Gedächtnislose Binärquelle
$\text{Fazit:}$
- Bei statistischer Unabhängigkeit der Folgenelemente ist $H = H_2 = H_1 \le H_0$.
- Bei statistischer Abhängigkeit der Folgenelemente gilt dagegen $H < H_2 < H_1 \le H_0$.
$\text{Zusammenfassung der Ergebnisse der letzten Seiten:}$
- Allgemein gilt für die Entropie einer Nachrichtenquelle:
- $$H \le \text{...} \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$
- Eine redundanzfreie Quelle liegt vor, falls alle $M$ Symbole gleichwahrscheinlich sind und es keine statistischen Bindungen innerhalb der Folge gibt.
Für diese gilt ( $r$ bezeichnet hierbei die relative Redundanz ):
- $$H = H_0 = H_1 = H_2 = H_3 = \text{...}\hspace{0.5cm} \Rightarrow \hspace{0.5cm} r = \frac{H - H_0}{H_0}= 0 \hspace{0.05cm}.$$
- Eine gedächtnislose Quelle kann durchaus redundant sein $(r> 0)$. Diese Redundanz geht dann allein auf die Abweichung der Symbolwahrscheinlichkeiten von der Gleichverteilung zurück. Hier gelten folgende Relationen:
- $$H = H_1 = H_2 = H_3 = \text{...} \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}0 \le r = \frac{H_1 - H_0}{H_0}< 1 \hspace{0.05cm}.$$
- Die entsprechende Bedingung für eine gedächtnisbehaftete Quelle lautet:
- $$ H <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 0 < r = \frac{H_1 - H_0}{H_0}\le1 \hspace{0.05cm}.$$
- Ist $H_2 < H_1$, dann gilt auch $H_3 < H_2$, $H_4 < H_3$, usw. ⇒ In der allgemeinen Gleichung ist also das „≤”–Zeichen durch das „<”–Zeichen zu ersetzen.
- Sind die Symbole gleichwahrscheinlich, so gilt wieder $H_1 = H_0$, während bei nicht gleichwahrscheinlichen Symbolen $H_1 < H_0$ zutrifft.
$\text{Fazit:}$ Bildet man den Grenzübergang für $k \to \infty$, so erhält man für die tatsächliche Quellenentropie:
- $$H = \lim_{k \rightarrow \infty } H_k = H_{\rm M} \hspace{0.05cm}.$$
Aus diesem einfachen Ergebnis folgen wichtige Erkenntnisse für die Entropieberechnung:
- Bei Markovquellen genügt die Bestimmung der Entropienäherungen $H_1$ und $H_2$. Damit lautet die Entropie einer Markovquelle:
- $$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm}.$$
- Durch $H_1$ und $H_2$ liegen auch alle weiteren Entropienäherungen $H_k$ für $k \ge 3$ fest:
- $$H_k = \frac{2-k}{k} \cdot H_{\rm 1} + \frac{2\cdot (k-1)}{k} \cdot H_{\rm 2} \hspace{0.05cm}.$$
Diese Näherungen haben allerdings keine große Bedeutung. Wichtig ist meist nur der Grenzwert $H$. Bei Quellen ohne Markoveigenschaften berechnet man die Näherungen $H_k$ nur deshalb, um den Grenzwert, also die tatsächliche Entropie, abschätzen zu können.
Hierbei wird der Vorteil von Markovquellen gegenüber anderen Quellen ausgenutzt, dass sich die Entropieberechnung für $k$–Tupel sehr einfach gestaltet.
- $$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_2 = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big ]\hspace{0.05cm}, \hspace{0.3cm} H_3 ={1}/{3} \cdot \big [ H_{\rm 1} + 2 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.3cm} H_4 = {1}/{4} \cdot \big [ H_{\rm 1} + 3 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.15cm}{\rm usw.}$$
Zu diesem Beispiel ist noch anzumerken:
- Hätte man nicht die Markoveigenschaften der roten und der grünen Folge ausgenutzt, so hätte man das Ergebnis $H ≈ 0.72 \hspace{0.05cm} \rm bit/Symbol$ erst nach langwierigen Berechnungen erhalten.
- Auf den nächsten Seiten wird gezeigt, dass bei einer Quelle mit Markoveigenschaften der Endwert $H$ allein aus den Entropienäherungen $H_1$ und $H_2$ ermittelt werden kann. Ebenso lassen sich aus $H_1$ und $H_2$ alle Entropienäherungen $H_k$ für $k$–Tupel in einfacher Weise berechnen ⇒ $H_3$, $H_4$, $H_5$, ... , $H_{100}$, ...
Anzumerken ist:
- Der erste Summand $H_1$ ⇒ erste Entropienäherung ist allein abhängig von den Symbolwahrscheinlichkeiten.
- Bei einem symmetrischen Markovprozess ⇒ $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} $ ⇒ $p_{\text{A}} = p_{\text{B}} = 1/2$ ergibt sich für diesen ersten Summanden $H_1 = 1 \hspace{0.05cm} \rm bit/Symbol$.
- Der zweite Summand $H_{\text{M}}$ muss gemäß der zweiten der oberen Gleichungen berechnet werden.
- Bei einem symmetrischen Markovprozess erhält man $H_{\text{M}} = H_{\text{bin}}(p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}})$.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2007 von Thomas Großer im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018 wurde das Programm von Marwen Ben Ammar und Xiaohan Liu (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.