Aufgaben:Aufgabe 4.12: Wurzel–Nyquist–Systeme

• Zurück zum Buch

Spektren von Sendegrundimpuls und Detektionsgrundimpuls

Bei Quadraturamplitudenmodulationssystemen wird häufig anstelle eines rechteckförmigen Sendegrundimpulses die  Wurzel–Nyquist–Variante  gewählt, wobei dieser Name aus dem Spektralbereich abgeleitet ist. Der Grund hierfür ist die signifikant kleinere Bandbreite.

• In diesem Fall erfüllt der Detektionsgrundimpuls  $g_d(t)$  die  erste Nyquistbedingung, da  $G_d(f)$  punktsymmetrisch um die so genannte Nyquistfrequenz  $f_{\rm Nyq} = 1/T$ ist.
• Die Spektralfunktion $G_d(f)$  ist ein  Cosinus–Rolloff–Spektrum, wobei der Rolloff–Faktor  $r$  Werte zwischen  $0$  und  $1$  (einschließlich dieser Grenzen) annehmen kann.

Weiterhin gilt für den Nyquist–Frequenzgang:

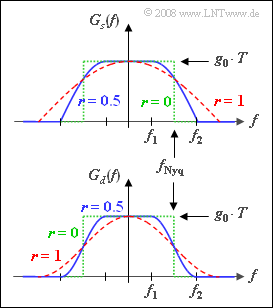
• Für  $|f| < f_1 = f_{\rm Nyq} · (1 – r)$  ist  $G_d(f)$  konstant gleich  $g_0 · T$.
• Bei Frequenzen größer als  $f_2 = f_{\rm Nyq} · (1 + r)$  hat  $G_d(f)$  keine Anteile.
• Dazwischen verläuft die Flanke cosinusförmig.

Die Optimierung digitaler Nachrichtenübertragungssysteme ergibt, dass der Empfängerfrequenzgang  $H_{\rm E}(f)$  formgleich mit dem Sendespektrum  $G_s(f)$  sein sollte.

Um dimensionsrichtige Spektralfunktionen zu erhalten, wird für diese Aufgabe und die Grafik vorausgesetzt:

$$G_s(f) = \sqrt{g_0 \cdot T \cdot G_d(f)},\hspace{0.4cm} H_{\rm E}(f) = \frac{1}{g_0 \cdot T}\cdot G_s(f)\hspace{0.05cm}.$$

Die obere Grafik zeigt das Sendespektrum  $G_s(f)$  für die Rolloff–Faktoren

• $r = 0$  (grün punktiertes Rechteck),
• $r = 0.5$  (blaue durchgezogene Kurve),
• $r = 1$  (rote gestrichelte Kurve).

Unten ist das Spektrum $G_d(f)$ vor dem Entscheider in gleichen Farben dargestellt.

• Der dazugehörige Impuls $g_d(t)$ ist für alle gültigen Rolloff–Faktoren ($0 ≤ r ≤ 1$) ein Nyquistimpuls im Gegensatz zum Sendegrundimpuls $g_s(t)$.
• Für diesen wird in der Literatur – zum Beispiel in [Kam04] – folgende Gleichung angegeben:

$$g_s(t) = g_0 \cdot \frac{4 r t/T \cdot \cos \left [\pi \cdot (1+r) \cdot t/T \right ]+ \sin \left [\pi \cdot (1-r) \cdot t/T \right ]}{\left [1- (4 r t/T)^2 \right ] \cdot \pi \cdot t/T}\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Quadratur–Amplitudenmodulation.
• Bezug genommen wird insbesondere auf die Seite  Nyquist- und Wurzel-Nyquist-Systeme  in diesem Kapitel.
• Weitere hilfreiche Informationen erfahren Sie im Kapitel  Eigenschaften von Nyquistsystemen  des Buches „Digitalsignalübertragung”.
• [Kam04] verweist auf das Fachbuch „Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004”.
• Energien sind in  $\rm V^2s$  anzugeben; sie beziehen sich somit auf den Bezugswiderstand  $R = 1 \ \rm \Omega$.

Fragebogen

1

Wie lautet der Sendegrundimpuls  $g_s(t)$  für den Rolloff–Faktor  $r = 0$? Welcher Signalwert ergibt sich zum Zeitpunkt  $t = 0$?

$g_s(t = 0) \ = \ $ $\ \cdot g_0$

2

Wie lautet der Sendegrundimpuls  $g_s(t)$  für den Rolloff–Faktor  $r = 1$? Welcher Signalwert ergibt sich zum Zeitpunkt  $t = 0$?

$g_s(t = 0) \ = \ $ $\ \cdot g_0$

3

Es gelte weiter  $r = 1$. Zu welchen Zeiten hat  $g_s(t)$  Nulldurchgänge?

	Bei allen Vielfachen der Symboldauer  $T$.
	Bei  $t = ±0.25 T, \ ±0.75 T, \ ±1.25 T, \ ±1.75 T$, ...
	Bei  $t = ±0.75 T, \ ±1.25 T,\ ±1.75 T$, ...

4

Wie lautet der Sendegrundimpuls  $g_s(t)$  für den Rolloff–Faktor  $r = 0.5$? Welcher Signalwert ergibt sich zum Zeitpunkt  $t = 0$?

$g_s(t = 0) \ = \ $ $\ \cdot g_0$

5

Welche Aussagen sind für die Signalamplitude unabhängig von  $r$  gültig? Lösen Sie diese Teilaufgabe im Frequenzbereich.

	Die Sendeimpulsamplitude kann alle Werte im Bereich  $0 ≤ g_s(t = 0) ≤ g_0$  annehmen.
	Die Sendeimpulsamplitude kann alle Werte im Bereich  $g_0 ≤ g_s(t = 0) ≤ 2 g_0$  annehmen.
	Die Sendeimpulsamplitude kann alle Werte im Bereich  $g_0 ≤ g_s(t = 0) ≤ 4 g_0/π$  annehmen.

6

Wie groß ist die Energie  $E_{g_s}$  des Sendegrundimpulses  $g_s(t)$  für  $r = 0$  und  $r = 1$?

$r = 0\text{:} \ \ \ \ E_{g_s} \ = \ $ $\ \cdot g_0^2 \cdot T$

$r = 1\text{:} \ \ \ \ E_{g_s} \ = \ $ $\ \cdot g_0^2 \cdot T$

Musterlösung

Musterlösung

(1)  Setzt man in die gegebene Gleichung $r = 0$ ein, so verschwinden im Zähler und Nenner die jeweils ersten Terme und man erhält:

$$g_s(t) = g_0 \cdot \frac{\sin \left (\pi \cdot t/T \right )}{\pi \cdot t/T} = g_0 \cdot {\rm si} \left (\pi \cdot {t}/{T} \right )\hspace{0.05cm}.$$

Zum Zeitpunkt $t = 0$ ist der si–Impuls gleich $g_0$:   $ g_s(t) \hspace{0.15cm}\underline { = 1.0 } \cdot g_0 \hspace{0.05cm}.$

(2)  Für $r = 1$ lässt sich die angegebene Gleichung wie folgt vereinfachen:

$$g_s(t) = \frac{4 \cdot g_0}{\pi} \cdot \frac{ \cos \left (2 \pi \cdot t/T \right )}{\left [1- (4 t/T)^2 \right ] }\hspace{0.3cm}\Rightarrow \hspace{0.3cm} g_s(t = 0) = \frac{4 \cdot g_0}{\pi} \hspace{0.15cm}\underline {= 1.273 }\cdot g_0 \hspace{0.05cm}.$$

(3)  Richtig ist der letzte Lösungsvorschlag:

• Nulldurchgänge sind für $r = 1$ nur möglich, wenn die Cosinusfunktion im Zähler Null ist, also für alle ganzzahligen Werte von $k$:

$$2 \pi \cdot t/T = {\pi}/{2} + k \cdot \pi \hspace{0.3cm}\Rightarrow \hspace{0.3cm} t = \pm 0.25T, \hspace{0.15cm} \pm 0.75T, \hspace{0.15cm}\pm 1.25T, \hspace{0.15cm} ...$$

• Richtig ist aber nur der letzte Lösungsvorschlag, da die Nullstellen bei $±0.25T$ durch die Nullstelle im Nenner aufgehoben werden.
• Die Anwendung der Regel von de l'Hospital liefert $g_s(t = ± 0.25T) = g_0$.

(4)  Mit $r = 0.5$ und der Abkürzung $x = t/T$ erhält man:

$$g_s(x) = \frac{g_0}{\pi} \cdot \frac{2 \cdot x \cdot \cos \left (1.5\pi \cdot x \right )+ \sin \left (0.5\pi \cdot x \right )}{\left (1- 4 \cdot x^2 \right ) \cdot x}\hspace{0.05cm}.$$

• Für die Berechnung zum Zeitpunkt $t = 0$ muss die Regel von de l'Hospital angewandt werden.
• Die Ableitungen von Zähler und Nenner ergeben:

$$Z'(x) = 2 \cdot \cos \left (1.5\pi \cdot x \right ) - 3 \pi \cdot x \cdot \sin \left (1.5\pi \cdot x \right ) + 0.5 \pi \cdot \cos \left (0.5\pi \cdot x \right ),$$

$$N'(x) = \left (1- 4 \cdot x^2 \right ) - 8 \cdot x^2 \hspace{0.05cm}.$$

• Die beiden Grenzübergänge für $x → 0$ liefern:

$$\lim_{x \rightarrow 0} Z'(x) = 2 +{\pi }/{2},\hspace{0.2cm} \lim_{x \rightarrow 0} N'(x) = 1 \hspace{0.05cm}.$$

• Damit gilt für die Signalamplitude zum Zeitpunkt $t = 0$:

$$g_s(t=0) = \frac{g_0}{\pi} \cdot \left ( 2 +{\pi }/{2} \right ) = {g_0} \cdot \left ( 0.5 + {2}/{\pi } \right )\hspace{0.15cm}\underline {= 1.137} \cdot g_0 \hspace{0.05cm}.$$

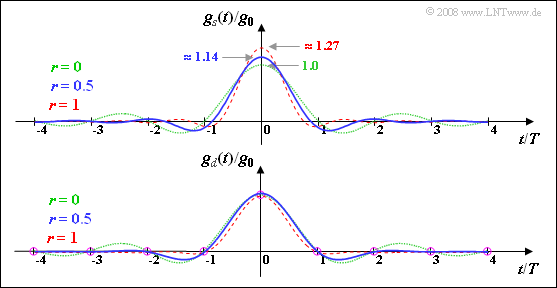
Die Grafik verdeutlicht nochmals die hier berechneten Ergebnisse:

• Der Impuls $g_d(t)$ ist ein Nyquistimpuls, das heißt, dass er besitzt zumindest bei allen Vielfachen der Symboldauer $T$ Nulldurchgänge (je nach Rolloff–Faktor noch andere Nullstellen).
• Der Sendegrundimpuls $g_s(t)$ erfüllt dagegen die Nyquistbedingung nicht.
• Außerdem erkennt man aus dieser Darstellung nochmals, dass für $r ≠ 0$ die Impulsamplitude $g_s(t = 0)$ stets größer als $g_0$ ist.

Sendegrundimpuls (Wurzel–Nyquist) und Detektionsgrundimpuls (Nyquist)

(5)  Richtig ist der letzte Lösungsvorschlag:

• Der erste Lösungsvorschlag scheidet bereits nach den Ergebnissen der Teilaufgaben (2) und (4) aus.

Die Gültigkeit der unteren Schranke $g_0$ und der oberen Schranke $4g_0/π$ lässt sich wie folgt nachweisen:

• Die Impulsamplitude $g_s(t = 0)$ ist grundsätzlich gleich der Fläche unter der Spektralfunktion $G_s(f)$.
• Die kleinste Fläche ergibt sich für $r = 0$. Hier ist $G_s(f) = g_0 · T$ im Bereich $|f| < ±1/(2T)$. Die Fläche ist somit gleich $g_0$.
• Die größte Fläche ergibt sich für $r = 1$. Hier ist $G_s(f)$ auf den Bereich $±1/T$ ausgedehnt und hat einen cosinusförmigen Verlauf.
• Das Ergebnis $g_s(t = 0) = 4g_0/π$ wurde bereits in Teilaufgabe (3) berechnet. Es gilt aber auch:

$$g_s(t=0) = 2 \cdot {g_0} \cdot \int_{ 0 }^{1/T} {\cos\left(\frac{\pi }{2}\cdot f \cdot T \right)}\hspace{0.1cm} {\rm d}f = \frac{4 g_0}{\pi} \cdot \int_{ 0 }^{\pi/2} {\cos\left(x \right)}\hspace{0.1cm} {\rm d}x = {4 g_0}/{\pi} \cdot \big[\sin(\pi/2) - \sin(0) \big] = {4 g_0}/{\pi}\hspace{0.05cm}.$$

(6)  Die Energie des Sendegrundimpulses $g_s(t)$ kann man nach dem Satz von Parseval im Zeit– oder auch im Frequenzbereich ermitteln:

$$E_{g_s} = \int_{ -\infty }^{+\infty} {[g_s(t)]^2}\hspace{0.1cm} {\rm d}t = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$

• Aus den Gleichungen und der Grafik auf der Angabenseite erkennt man, dass $|G_s(f)|^2$ formgleich mit $G_d(f)$ ist, mit dem Unterschied, dass die Höhe nun $(g_0 · T)^2$ anstelle von $g_0 · T$ ist:

$$E_{g_s} = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f = \frac{g_0^2 \cdot T^2}{g_0 \cdot T} \cdot \int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$

• Aufgrund der Nyquistform von $G_d(f)$ gilt aber unabhängig von $r$:

$$\int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f = g_0 \hspace{0.05cm}.$$

• Damit ist auch die Impulsenergie unabhängig von $r$, also auch gültig für $r = 0$ und $r = 1$. In beiden Fällen ist

$$E_ {g_s}\hspace{0.15cm}\underline { = 1.0} · g_0^2 · T.$$