Aufgaben:Aufgabe 4.10: Union Bound

• Zurück zum Buch

Signalraumkonstellationen mit $N=2$  und  $M=3$

Die  „Union Bound”  ist eine obere Schranke für die Fehlerwahrscheinlichkeit eines nichtbinären Übertragungssystems  $(M > 2)$.

• Die tatsächliche  (mittlere)  Fehlerwahrscheinlichkeit ist allgemein wie folgt gegeben:

$${\rm Pr}({ \cal E}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sum\limits_{i = 0 }^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.05cm},$$

$$ {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] \hspace{0.05cm},\hspace{0.2cm}{ \rm wobei}\hspace{0.2cm} { \cal E}_{ik}\text{:} \ \ \boldsymbol{ r }{\rm \hspace{0.15cm}liegt \hspace{0.15cm}n\ddot{a}her \hspace{0.15cm}bei \hspace{0.15cm}}\boldsymbol{ s }_k {\rm \hspace{0.15cm}als \hspace{0.15cm}beim \hspace{0.15cm}Sollwert \hspace{0.15cm}}\boldsymbol{ s }_i \hspace{0.05cm}.$$

• Die einfachere  "Union Bound"  liefert eine obere Schranke für die Verfälschungswahrscheinlichkeit unter der Voraussetzung,  dass die Nachricht  $m_i$  $($bzw. das Signal  $\boldsymbol{s}_i)$  gesendet wurde:

$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ \ge \ \hspace{-0.1cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s }_i ) = {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i )\hspace{0.05cm},\ $$

$$ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \hspace{-0.1cm} \ = \ \hspace{-0.2cm}\sum\limits_{k = 0 ,\hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm} {\rm Pr}({ \cal E}_{ik}) = \hspace{-0.1cm}\sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}\hspace{-0.1cm}{\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right )\hspace{0.05cm}. $$

Dabei sind folgende Abkürzungen verwendet:

• ${\rm Q}(x)$  ist die komplementäre Gaußsche Fehlerfunktion;

• $d_{ik}$  bezeichnet den Abstand der Signalpunkte  $\boldsymbol{s}_i$  und  $\boldsymbol{s}_k$;

• $\sigma_n$  ist der Effektivwert  (⇒ Wurzel aus der Varianz)  des additiven weißen Gaußschen Rauschens.

⇒   Durch Mittelung über alle möglichen Signale  $\boldsymbol{s}_i$  kommt man dann zur eigentlichen  "Union Bound" :

$$p_{\rm UB} = \sum\limits_{i = 0 }^{M-1} {\rm Pr}(\boldsymbol{ s }_i) \cdot p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_i} \ge {\rm Pr}({ \cal E}) \hspace{0.05cm}.$$

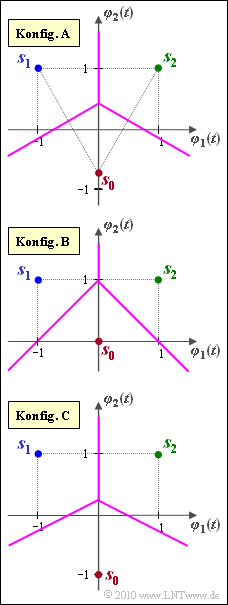
Die Grafik zeigt drei verschiedene Signalraumkonstellationen mit jeweils  $M = 3$  Signalraumpunkten  $\boldsymbol{s}_0$,  $\boldsymbol{s}_1$  und  $\boldsymbol{s}_2$  im zweidimensionalen Raum  $(N = 2)$.

• Die Basisfunktionen  $\varphi_1(t)$  und  $\varphi_2(t)$  sind geeignet normiert.

• Somit sind auch die Signalraumkoordinaten reine Zahlenwerte ohne Einheit:

$$\boldsymbol{ s }_1 = (-1, \hspace{0.1cm}+1)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_2 = (+1, \hspace{0.1cm}+1)\hspace{0.05cm}.$$

• Der Signalraumpunkt  $\boldsymbol{s}_0$  in der Konfiguration  $\rm A$  liegt so, dass  $\boldsymbol{s}_0$,  $\boldsymbol{s}_1$,  $\boldsymbol{s}_2$  ein gleichseitiges Dreieck beschreiben.

• Bei den Konfigurationen  $\rm B$  und  $\rm C$  gilt dagegen  $\boldsymbol{s}_0 = (0,\ 0)$  bzw.  $\boldsymbol{s}_0 = (0, \ –1)$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  "Approximation der Fehlerwahrscheinlichkeit".

• Verwenden Sie für alle Berechnungen den AWGN–Effektivwert  $\sigma_n = 0.5$.

• Gegeben sind folgende Werte der komplementären Gaußschen Fehlerfunktion:

$${\rm Q}(1) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.159\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(\sqrt{2}) \approx 0.079\hspace{0.05cm}, \hspace{0.23cm}{\rm Q}(\sqrt{3}) \approx 0.042\hspace{0.05cm},$$

$${\rm Q}(2) \hspace{-0.1cm} \ \approx \ \hspace{-0.1cm} 0.023\hspace{0.05cm}, \hspace{0.2cm}{\rm Q}(2.14) \approx 0.016\hspace{0.05cm}, \hspace{0.1cm}{\rm Q}(\sqrt{5}) \approx 0.013 \hspace{0.05cm}.$$

Fragebogen

1

Welche der drei Konfigurationen führt zur kleinsten Fehlerwahrscheinlichkeit  $($zumindest nach der  "Union Bound"–Näherung)?

	Konfiguration  $\rm A$,
	Konfiguration  $\rm B$,
	Konfiguration  $\rm C$.

2

Berechnen Sie die  „gemittelte Union Bound”   $(p_{\rm UB})$  für die Konfiguration  $\rm A$.

$p_{\rm UB} \ = \ $ $\ \%$

3

Berechnen Sie die  „gemittelte Union Bound”  für die Konfiguration  $\rm B$.

$p_{\rm UB} \ = \ $ $\ \%$

4

Berechnen Sie die  „gemittelte Union Bound”  für die Konfiguration  $\rm C$.

$p_{\rm UB} \ = \ $ $\ \%$

5

Wie müsste der Rauscheffektivwert  $\sigma_n$  bei Konfiguration  $\rm A$  verändert werden,  damit sich die gleiche  "Union Bound"  wie in Aufgabe  (4)  ergibt?

$\sigma_n \ = \ $

Musterlösung

Musterlösung

(1)  Die Punkte $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ sind für alle Konfigurationen gleich.

• Die kleinste Fehlerwahrscheinlichkeit ergibt sich, wenn $\boldsymbol{s}_0$ von $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ am weitesten entfernt liegt.
• Dies ist bei der Konfiguration C der Fall   ⇒   Lösungsvorschlag 3.

(2)  Bei der Konfiguration A ist der Abstand zwischen allen Punkten gleich: $d_{01} = d_{02} = d_{12} = 2$.

• Deshalb muss zur Berechnung der Union Bound nicht über alle Symbole gemittelt werden, und es gilt, da zum Beispiel $\boldsymbol{s}_0$ mit gleicher Wahrscheinlichkeit in das Symbol $\boldsymbol{s}_1$ bzw. $\boldsymbol{s}_2$ verfälscht wird:

$${\rm Pr}({ \cal E}) \le p_{\rm UB} = 2 \cdot {\rm Q} \left ( \frac{d_{ik}/2}{\sigma_n} \right ) = 2 \cdot {\rm Q}(2) \approx 2 \cdot 0.023 \hspace{0.1cm}\hspace{0.15cm}\underline {= 4.6\%} \hspace{0.05cm}. $$

(3)  Hier unterscheiden sich die Verfälschungswahrscheinlichkeiten für die einzelnen Symbole.

• Wurde $\boldsymbol{s}_0$ gesendet, so gilt mit $d_{01} = d_{02} = 2^{0.5}$ und $\sigma = 0.5$:

$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_0} = 2 \cdot {\rm Q} \left ( \frac{\sqrt{2}/2}{0.5} \right ) = 2 \cdot {\rm Q}(\sqrt{2}) = 2 \cdot 0.079 = 0.158 \hspace{0.05cm}. $$

• Dagegen sind die beiden anderen bedingten Wahrscheinlichkeiten kleiner:

$$p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_1} = p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Q} \left ( \frac{{2}/2}{0.5} \right )+{\rm Q} \left ( \frac{\sqrt{2}/2}{0.5} \right )= {\rm Q}(2) +{\rm Q}(\sqrt{2}) = 0.023 + 0.079 = 0.102 \hspace{0.05cm}.$$

Durch Mittelung erhält man für die Union Bound unter Berücksichtigung der unterschiedlichen Abstände:

$$p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{3} \cdot \left [ p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_0} + p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_1} +p_{{\rm UB}\hspace{0.05cm}| \hspace{0.05cm}\boldsymbol{ s }_2}\right ]= {1}/{3} \cdot \left [ 2 \cdot {\rm Q}(\sqrt{2})+ 2 \cdot ({\rm Q}({2}) + {\rm Q}(\sqrt{2})) \right ] = {1}/{3} \cdot \left [ 4 \cdot {\rm Q}(\sqrt{2})+ 2 \cdot {\rm Q}({2}) \right ] $$

$$ \Rightarrow \hspace{0.3cm} p_{\rm UB} = {1}/{3} \cdot \left [ 4 \cdot 0.079+ 2 \cdot 0.023 \right ] \hspace{0.1cm}\hspace{0.12cm}\underline {\approx 12.1\% } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm UB}\ge {\rm Pr}({ \cal E})\hspace{0.05cm}.$$

(4)  Diese Konfiguration wird durch folgende Gleichungen beschrieben:

$$d_{01} = d_{02} = \sqrt{2^2 + 1^2}= \sqrt{5} \approx 2.24\hspace{0.2cm}, d_{12} = 2$$

$$\Rightarrow \hspace{0.3cm} p_{\rm UB} = {1}/{3} \cdot \left [ 4 \cdot {\rm Q}(\sqrt{5})+ 2 \cdot {\rm Q}({2}) \right ] = {1}/{3} \cdot \left [ 4 \cdot 0.013+ 2 \cdot 0.023 \right ]\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 3.2\%} \hspace{0.05cm}. $$

(5)  Es soll gelten:

$$p_{\rm UB} = 2 \cdot {\rm Q}\left ( {1}/{\sigma_n} \right ) = 0.032 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q}\left ( {1}/{\sigma_n} \right ) = 0.016\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {1}/{\sigma_n} \approx 2.14 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.1cm}\hspace{0.15cm}\sigma_n \hspace{0.15cm}\underline {\approx 0.467}\hspace{0.05cm}. $$