Applets:WDF, VTF und Momente spezieller Verteilungen (Applet): Unterschied zwischen den Versionen
| Zeile 28: | Zeile 28: | ||
In diesem Applet betrachten wir ausschließlich ''(wert–)kontinuierliche Zufallsgrößen'', also solche, deren mögliche Zahlenwerte nicht abzählbar sind. Zumindest in gewissen Intervallen ... '''???''' | In diesem Applet betrachten wir ausschließlich ''(wert–)kontinuierliche Zufallsgrößen'', also solche, deren mögliche Zahlenwerte nicht abzählbar sind. Zumindest in gewissen Intervallen ... '''???''' | ||
Alle Beispiele Gauß | Alle Beispiele Gauß | ||
| + | <br><br> | ||
| + | |||
===Wahrscheinlichkeitsdichtefunktion (WDF)=== | ===Wahrscheinlichkeitsdichtefunktion (WDF)=== | ||
Bei einer kontinuierlichen Zufallsgröße $X$ sind die Wahrscheinlichkeiten, dass $X$ ganz bestimmte Werte $x$ annimmt, identisch Null: ${\rm Pr}(X= x) \equiv 0$. Deshalb muss zur Beschreibung einer kontinuierlichen Zufallsgröße stets auf die ''Wahrscheinlichkeitsdichtefunktion'' – abgekürzt $\rm WDF$ – übergegangen werden. | Bei einer kontinuierlichen Zufallsgröße $X$ sind die Wahrscheinlichkeiten, dass $X$ ganz bestimmte Werte $x$ annimmt, identisch Null: ${\rm Pr}(X= x) \equiv 0$. Deshalb muss zur Beschreibung einer kontinuierlichen Zufallsgröße stets auf die ''Wahrscheinlichkeitsdichtefunktion'' – abgekürzt $\rm WDF$ – übergegangen werden. | ||
| Zeile 45: | Zeile 47: | ||
*Als wichtige Normierungseigenschaft ergibt sich daraus für die Fläche unter der WDF mit den Grenzübergängen $x_{\rm u} → \hspace{0.1cm} – \hspace{0.05cm} ∞$ und $x_{\rm o} → +∞$: | *Als wichtige Normierungseigenschaft ergibt sich daraus für die Fläche unter der WDF mit den Grenzübergängen $x_{\rm u} → \hspace{0.1cm} – \hspace{0.05cm} ∞$ und $x_{\rm o} → +∞$: | ||
:$$\int_{-\infty}^{+\infty} f_{X}(x) \ {\rm d}x = 1.$$ | :$$\int_{-\infty}^{+\infty} f_{X}(x) \ {\rm d}x = 1.$$ | ||
| + | <br> | ||
| + | |||
| + | ===Verteilungsfunktion (VTF)=== | ||
| + | |||
| + | Die ''Verteilungsfunktion'' – abgekürzt $\rm VTF$ – liefert die gleiche Information über die Zufallsgröße $X$ wie die Wahrscheinlichkeitsdichtefunktion. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ Die '''Verteilungsfunktion''' $F_{X}(x)$ entspricht der Wahrscheinlichkeit, dass die Zufallsgröße $X$ kleiner oder gleich einem reellen Zahlenwert $x$ ist: | ||
| + | :$$F_{X}(x) = {\rm Pr}( X \le x).$$ | ||
| + | |||
| + | Die englische Bezeichnung für die Verteilungsfunktion (VTF) ist ''Cumulative Distribution Function'' (CDF). }} | ||
| + | |||
| + | |||
| + | Die VTF weist folgende Eigenschaften auf: | ||
| + | |||
| + | *Die Verteilungsfunktion ist aus der Wahrscheinlichkeitsdichtefunktion $f_{X}(x)$ durch Integration berechenbar. Es gilt: | ||
| + | :$$F_{X}(x) = \int_{-\infty}^{x}f_X(\xi)\,{\rm d}\xi.$$ | ||
| + | *Da die WDF nie negativ ist, steigt $F_{X}(x)$ zumindest schwach monoton an, und liegt stets zwischen den folgenden Grenzwerten | ||
| + | :$$F_{X}(x → \hspace{0.1cm} – \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{X}(x → +∞) = 1.$$ | ||
| + | *Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch Differentiation bestimmen: | ||
| + | :$$f_{X}(x)=\frac{{\rm d} F_{X}(\xi)}{{\rm d}\xi}\Bigg |_{\hspace{0.1cm}x=\xi}.$$ | ||
| + | *Für die Wahrscheinlichkeit, dass die Zufallsgröße $X$ im Bereich zwischen $x_{\rm u}$ und $x_{\rm o} > x_{\rm u}$ liegt, gilt: | ||
| + | :$${\rm Pr}(x_{\rm u} \le X \le x_{\rm o}) = F_{X}(x_{\rm o}) - F_{X}(x_{\rm u}).$$ | ||
| + | <br> | ||
| + | |||
| + | ===Erwartungswerte und Momente=== | ||
| + | Die Wahrscheinlichkeitsdichtefunktion bietet ebenso wie die Verteilungsfunktion sehr weitreichende Informationen über die betrachtete Zufallsgröße. Weniger, aber dafür kompaktere Informationen liefern die so genannten ''Erwartungswerte'' und ''Momente.'' | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ Der '''Erwartungswert''' bezüglich einer beliebigen Gewichtungsfunktion $g(x)$ kann mit der WDF $f_{\rm X}(x)$ in folgender Weise berechnet werden: | ||
| + | :$${\rm E}\big[g (X ) \big] = \int_{-\infty}^{+\infty} g(x)\cdot f_{X}(x) \,{\rm d}x.$$ | ||
| + | Setzt man in diese Gleichung für $g(X) = x^k$ ein, so erhält man das '''Moment $k$-ter Ordnung''': | ||
| + | :$$m_k = {\rm E}\big[x^k \big] = \int_{-\infty}^{+\infty} x^k\cdot f_{X} (x ) \, {\rm d}x.$$}} | ||
| + | |||
| + | |||
| + | Aus dieser Gleichung erhält man | ||
| + | *mit $k = 1$ für den '''linearen Mittelwert''': | ||
| + | :$$m_1 = {\rm E}\big[X \big] = \int_{-\infty}^{ \rm +\infty} x\cdot f_{X} (x ) \,{\rm d}x,$$ | ||
| + | *mit $k = 2$ für den '''quadratischen Mittelwert''': | ||
| + | :$$m_2 = {\rm E}\big[X^{\rm 2} \big] = \int_{-\infty}^{ \rm +\infty} x^{ 2}\cdot f_{ X} (x) \,{\rm d}x.$$ | ||
| + | |||
| + | In Zusammenhang mit Signalen sind auch folgende Bezeichnungen üblich: | ||
| + | * $m_1$ gibt den ''Gleichanteil'' an, | ||
| + | * $m_2$ entspricht der (auf den Einheitswiderstand $1 \ Ω$ bezogenen) ''Signalleistung''. | ||
| + | |||
| + | |||
| + | Bezeichnet $X$ beispielsweise eine Spannung, so hat nach diesen Gleichungen $m_1$ die Einheit ${\rm V}$ und $m_2$ die Einheit ${\rm V}^2.$ Will man die Leistung in „Watt” $\rm (W)$ angeben, so muss $m_2$ noch durch den Widerstandswert $R$ dividiert werden. | ||
| + | <br><br> | ||
| + | |||
| + | ===Zentralmomente=== | ||
| + | <br> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ Besonders große Bedeutung haben in der Statistik die '''Zentralmomente''', die im Gegensatz zu den herkömmlichen Momenten jeweils auf den Mittelwert $m_1$ bezogen sind: | ||
| + | |||
| + | :$$\mu_k = {\rm E}\big[(x-m_{\rm 1})^k\big] = \int_{-\infty}^{+\infty} (x-m_{\rm 1})^k\cdot f_x(x) \,\rm d \it x.$$}} | ||
| + | |||
| + | |||
| + | |||
| + | Die nichtzentrierten Momente $m_k$ kann man direkt in die zentrierten Momente $\mu_k$ umrechnen: | ||
| + | :$$\mu_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot m_\kappa \cdot (-m_1)^{k-\kappa}.$$ | ||
| + | |||
| + | Nach den allgemein gültigen Gleichungen der [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Momentenberechnung_als_Scharmittelwert|letzten Seite]] ergeben sich die formalen Größen $m_0 = 1$ und $\mu_0 = 1$. Für das Zentralmoment erster Ordnung gilt nach obiger Definition stets $\mu_1 = 0$. | ||
| + | |||
| + | In der Gegenrichtung gelten folgende Gleichungen für $k = 1$, $k = 2$, usw.: | ||
| + | :$$m_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot \mu_\kappa \cdot {m_1}^{k-\kappa}.$$ | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Alle Momente einer binären Zufallsgröße mit den Wahrscheinlichkeiten ${\rm Pr}(0) = 1 – p$ und ${\rm Pr}(1) = p$ sind gleich groß: | ||
| + | :$$m_1 = m_2 = m_3 = m_4 = \hspace{0.05cm}\text{...} \hspace{0.05cm}= p.$$ | ||
| + | Mit obigen Gleichungen erhält man dann für die ersten drei Zentralmomente: | ||
| + | :$$\mu_2 = m_2 - m_1^2 = p -p^2, $$ | ||
| + | :$$\mu_3 = m_3 - 3 \cdot m_2 \cdot m_1 + 2 \cdot m_1^3 = p - 3 \cdot p^2 + 2 \cdot p^3, $$ | ||
| + | :$$ \mu_4 = m_4 - 4 \cdot m_3 \cdot m_1 + 6 \cdot m_2 \cdot m_1^2 - 3 \cdot m_1^4 = p - 4 \cdot p^2 + 6 \cdot p^3- 3 \cdot p^4. $$}} | ||
| + | |||
| + | |||
| + | |||
| + | <br> | ||
| + | Die im letzten Abschnitt angegebenen Gleichungen gelten nur für wertkontinuierliche Zufallsgrößen und sollen hier durch ein Beispiel verdeutlicht werden. Im nächsten Abschnitt wird gezeigt, dass für [[Stochastische_Signaltheorie/Verteilungsfunktion#Verteilungsfunktion_bei_diskreten_Zufallsgr.C3.B6.C3.9Fen|diskrete Zufallsgrößen]] die Gleichungen etwas modifiziert werden müssen. | ||
Version vom 21. August 2019, 17:00 Uhr
Inhaltsverzeichnis
Programmbeschreibung
WDF, VTF und Momente spezieller Verteilungen
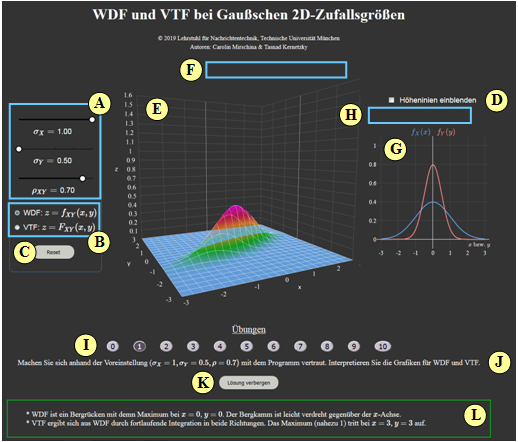
Das Applet verdeutlicht die Eigenschaften zweidimensionaler Gaußscher Zufallsgrößen $XY\hspace{-0.1cm}$, gekennzeichnet durch die Standardabweichungen (Streuungen) $\sigma_X$ und $\sigma_Y$ ihrer beiden Komponenten sowie den Korrelationskoeffizienten $\rho_{XY}$ zwischen diesen. Die Komponenten werden als mittelwertfrei vorausgesetzt: $m_X = m_Y = 0$.
Das Applet zeigt
- die zweidimensionale Wahrscheinlichkeitsdichtefunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{XY}(x, \hspace{0.1cm}y)$ in dreidimensionaler Darstellung sowie in Form von Höhenlinien,
- die zugehörigen Randwahrscheinlichkeitsdichtefunktionen $f_{X}(x)$ und $f_{Y}(y)$ ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}WDFs$,
- die zweidimensionale Verteilungsfunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{XY}(x, \hspace{0.1cm}y)$ als 3D-Plot.
Das Applet verwendet das Framework Plot.ly
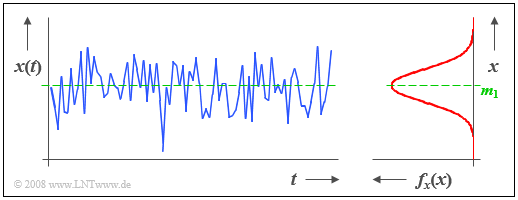
$\text{Beispiel 1:}$ Die Grafik zeigt einen Ausschnitt eines stochastischen Rauschsignals $x(t)$, dessen Momentanwert als eine kontinuierliche Zufallsgröße $x$ aufgefasst werden kann.
- Aus der rechts dargestellten Wahrscheinlichkeitsdichtefunktion (WDF) erkennt man, dass bei diesem Beispielsignal Momentanwerte um den Mittelwert $m_1$ am häufigsten auftreten.
- Da zwischen den Abtastwerten $x_ν$ keine statistischen Bindungen bestehen, bezeichnet man ein solches Signal auch als „Weißes Rauschen”.
Definition und Eigenschaften der dargestellten Beschreibungsgrößen
In diesem Applet betrachten wir ausschließlich (wert–)kontinuierliche Zufallsgrößen, also solche, deren mögliche Zahlenwerte nicht abzählbar sind. Zumindest in gewissen Intervallen ... ???
Alle Beispiele Gauß
Wahrscheinlichkeitsdichtefunktion (WDF)
Bei einer kontinuierlichen Zufallsgröße $X$ sind die Wahrscheinlichkeiten, dass $X$ ganz bestimmte Werte $x$ annimmt, identisch Null: ${\rm Pr}(X= x) \equiv 0$. Deshalb muss zur Beschreibung einer kontinuierlichen Zufallsgröße stets auf die Wahrscheinlichkeitsdichtefunktion – abgekürzt $\rm WDF$ – übergegangen werden.
$\text{Definition:}$ Der Wert der Wahrscheinlichkeitsdichtefunktion $f_{X}(x)$ an der Stelle $x$ ist gleich der Wahrscheinlichkeit, dass der Momentanwert der Zufallsgröße $X$ in einem (unendlich kleinen) Intervall der Breite $Δx$ um $x$ liegt, dividiert durch $Δx$:
- $$f_X(x) = \lim_{ {\rm \Delta} x \hspace{0.05cm}\to \hspace{0.05cm} 0} \frac{ {\rm Pr} \big [x - {\rm \Delta} x/2 \le X \le x +{\rm \Delta} x/2 \big ] }{ {\rm \Delta} x}.$$
Die englische Bezeichnung für die Wahrscheinlichkeitsdichtefunktion (WDF) ist Probability Density Function (PDF).
Die WDF weist folgende Eigenschaften auf:
- Für die Wahrscheinlichkeit, dass die Zufallsgröße $X$ im Bereich zwischen $x_{\rm u}$ und $x_{\rm o} > x_{\rm u}$ liegt, gilt:
- $${\rm Pr}(x_{\rm u} \le X \le x_{\rm o}) = \int_{x_{\rm u}}^{x_{\rm o}} f_{X}(x) \ {\rm d}x.$$
- Als wichtige Normierungseigenschaft ergibt sich daraus für die Fläche unter der WDF mit den Grenzübergängen $x_{\rm u} → \hspace{0.1cm} – \hspace{0.05cm} ∞$ und $x_{\rm o} → +∞$:
- $$\int_{-\infty}^{+\infty} f_{X}(x) \ {\rm d}x = 1.$$
Verteilungsfunktion (VTF)
Die Verteilungsfunktion – abgekürzt $\rm VTF$ – liefert die gleiche Information über die Zufallsgröße $X$ wie die Wahrscheinlichkeitsdichtefunktion.
$\text{Definition:}$ Die Verteilungsfunktion $F_{X}(x)$ entspricht der Wahrscheinlichkeit, dass die Zufallsgröße $X$ kleiner oder gleich einem reellen Zahlenwert $x$ ist:
- $$F_{X}(x) = {\rm Pr}( X \le x).$$
Die englische Bezeichnung für die Verteilungsfunktion (VTF) ist Cumulative Distribution Function (CDF).
Die VTF weist folgende Eigenschaften auf:
- Die Verteilungsfunktion ist aus der Wahrscheinlichkeitsdichtefunktion $f_{X}(x)$ durch Integration berechenbar. Es gilt:
- $$F_{X}(x) = \int_{-\infty}^{x}f_X(\xi)\,{\rm d}\xi.$$
- Da die WDF nie negativ ist, steigt $F_{X}(x)$ zumindest schwach monoton an, und liegt stets zwischen den folgenden Grenzwerten
- $$F_{X}(x → \hspace{0.1cm} – \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{X}(x → +∞) = 1.$$
- Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch Differentiation bestimmen:
- $$f_{X}(x)=\frac{{\rm d} F_{X}(\xi)}{{\rm d}\xi}\Bigg |_{\hspace{0.1cm}x=\xi}.$$
- Für die Wahrscheinlichkeit, dass die Zufallsgröße $X$ im Bereich zwischen $x_{\rm u}$ und $x_{\rm o} > x_{\rm u}$ liegt, gilt:
- $${\rm Pr}(x_{\rm u} \le X \le x_{\rm o}) = F_{X}(x_{\rm o}) - F_{X}(x_{\rm u}).$$
Erwartungswerte und Momente
Die Wahrscheinlichkeitsdichtefunktion bietet ebenso wie die Verteilungsfunktion sehr weitreichende Informationen über die betrachtete Zufallsgröße. Weniger, aber dafür kompaktere Informationen liefern die so genannten Erwartungswerte und Momente.
$\text{Definition:}$ Der Erwartungswert bezüglich einer beliebigen Gewichtungsfunktion $g(x)$ kann mit der WDF $f_{\rm X}(x)$ in folgender Weise berechnet werden:
- $${\rm E}\big[g (X ) \big] = \int_{-\infty}^{+\infty} g(x)\cdot f_{X}(x) \,{\rm d}x.$$
Setzt man in diese Gleichung für $g(X) = x^k$ ein, so erhält man das Moment $k$-ter Ordnung:
- $$m_k = {\rm E}\big[x^k \big] = \int_{-\infty}^{+\infty} x^k\cdot f_{X} (x ) \, {\rm d}x.$$
Aus dieser Gleichung erhält man
- mit $k = 1$ für den linearen Mittelwert:
- $$m_1 = {\rm E}\big[X \big] = \int_{-\infty}^{ \rm +\infty} x\cdot f_{X} (x ) \,{\rm d}x,$$
- mit $k = 2$ für den quadratischen Mittelwert:
- $$m_2 = {\rm E}\big[X^{\rm 2} \big] = \int_{-\infty}^{ \rm +\infty} x^{ 2}\cdot f_{ X} (x) \,{\rm d}x.$$
In Zusammenhang mit Signalen sind auch folgende Bezeichnungen üblich:
- $m_1$ gibt den Gleichanteil an,
- $m_2$ entspricht der (auf den Einheitswiderstand $1 \ Ω$ bezogenen) Signalleistung.
Bezeichnet $X$ beispielsweise eine Spannung, so hat nach diesen Gleichungen $m_1$ die Einheit ${\rm V}$ und $m_2$ die Einheit ${\rm V}^2.$ Will man die Leistung in „Watt” $\rm (W)$ angeben, so muss $m_2$ noch durch den Widerstandswert $R$ dividiert werden.
Zentralmomente
$\text{Definition:}$ Besonders große Bedeutung haben in der Statistik die Zentralmomente, die im Gegensatz zu den herkömmlichen Momenten jeweils auf den Mittelwert $m_1$ bezogen sind:
- $$\mu_k = {\rm E}\big[(x-m_{\rm 1})^k\big] = \int_{-\infty}^{+\infty} (x-m_{\rm 1})^k\cdot f_x(x) \,\rm d \it x.$$
Die nichtzentrierten Momente $m_k$ kann man direkt in die zentrierten Momente $\mu_k$ umrechnen:
- $$\mu_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot m_\kappa \cdot (-m_1)^{k-\kappa}.$$
Nach den allgemein gültigen Gleichungen der letzten Seite ergeben sich die formalen Größen $m_0 = 1$ und $\mu_0 = 1$. Für das Zentralmoment erster Ordnung gilt nach obiger Definition stets $\mu_1 = 0$.
In der Gegenrichtung gelten folgende Gleichungen für $k = 1$, $k = 2$, usw.:
- $$m_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot \mu_\kappa \cdot {m_1}^{k-\kappa}.$$
$\text{Beispiel 1:}$ Alle Momente einer binären Zufallsgröße mit den Wahrscheinlichkeiten ${\rm Pr}(0) = 1 – p$ und ${\rm Pr}(1) = p$ sind gleich groß:
- $$m_1 = m_2 = m_3 = m_4 = \hspace{0.05cm}\text{...} \hspace{0.05cm}= p.$$
Mit obigen Gleichungen erhält man dann für die ersten drei Zentralmomente:
- $$\mu_2 = m_2 - m_1^2 = p -p^2, $$
- $$\mu_3 = m_3 - 3 \cdot m_2 \cdot m_1 + 2 \cdot m_1^3 = p - 3 \cdot p^2 + 2 \cdot p^3, $$
- $$ \mu_4 = m_4 - 4 \cdot m_3 \cdot m_1 + 6 \cdot m_2 \cdot m_1^2 - 3 \cdot m_1^4 = p - 4 \cdot p^2 + 6 \cdot p^3- 3 \cdot p^4. $$
Die im letzten Abschnitt angegebenen Gleichungen gelten nur für wertkontinuierliche Zufallsgrößen und sollen hier durch ein Beispiel verdeutlicht werden. Im nächsten Abschnitt wird gezeigt, dass für diskrete Zufallsgrößen die Gleichungen etwas modifiziert werden müssen.
Theoretischer Hintergrund
Wahrscheinlichkeitsdichtefunktion (WDF)
Bei einer kontinuierlichen Zufallsgröße $X$ sind die Wahrscheinlichkeiten, dass diese ganz bestimmte Werte annimmt, identisch Null. Deshalb muss zur Beschreibung einer kontinuierlichen Zufallsgröße stets auf die Wahrscheinlichkeitsdichtefunktion – abgekürzt WDF – übergegangen werden.
Die englische Bezeichnung für die Wahrscheinlichkeitsdichtefunktion (WDF) ist Probability Density Function (PDF). }} Wir betrachten zwei wertkontinuierliche Zufallsgrößen $X$ und $Y\hspace{-0.1cm}$, zwischen denen statistische Abhängigkeiten bestehen können. Zur Beschreibung der Wechselbeziehungen zwischen diesen Größen ist es zweckmäßig, die beiden Komponenten zu einer zweidimensionalen Zufallsgröße $XY =(X, Y)$ zusammenzufassen. Dann gilt:
$\text{Definition:}$ Die Verbundwahrscheinlichkeitsdichtefunktion ist die Wahrscheinlichkeitsdichtefunktion (WDF, englisch: Probability Density Function, kurz: PDF) der zweidimensionalen Zufallsgröße $XY$ an der Stelle $(x, y)$:
- $$f_{XY}(x, \hspace{0.1cm}y) = \lim_{\left.{\Delta x\rightarrow 0 \atop {\Delta y\rightarrow 0} }\right.}\frac{ {\rm Pr}\big [ (x - {\rm \Delta} x/{\rm 2} \le X \le x + {\rm \Delta} x/{\rm 2}) \cap (y - {\rm \Delta} y/{\rm 2} \le Y \le y +{\rm \Delta}y/{\rm 2}) \big] }{ {\rm \Delta} \ x\cdot{\rm \Delta} y}.$$
- Die Verbundwahrscheinlichkeitsdichtefunktion oder kurz $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ ist eine Erweiterung der eindimensionalen WDF.
- $∩$ kennzeichnet die logische UND-Verknüpfung.
- $X$ und $Y$ bezeichnen die beiden Zufallsgrößen, und $x \in X$ sowie $y \in Y$ geben Realisierungen hiervon an.
- Die für dieses Applet verwendete Nomenklatur unterscheidet sich also geringfügig gegenüber der Beschreibung im Theorieteil.
Anhand dieser 2D–WDF $f_{XY}(x, y)$ werden auch statistische Abhängigkeiten innerhalb der zweidimensionalen Zufallsgröße $XY$ vollständig erfasst im Gegensatz zu den beiden eindimensionalen Dichtefunktionen ⇒ Randwahrscheinlichkeitsdichtefunktionen:
- $$f_{X}(x) = \int _{-\infty}^{+\infty} f_{XY}(x,y) \,\,{\rm d}y ,$$
- $$f_{Y}(y) = \int_{-\infty}^{+\infty} f_{XY}(x,y) \,\,{\rm d}x .$$
Diese beiden Randdichtefunktionen $f_X(x)$ und $f_Y(y)$
- liefern lediglich statistische Aussagen über die Einzelkomponenten $X$ bzw. $Y$,
- nicht jedoch über die Bindungen zwischen diesen.
Als quantitatives Maß für die linearen statistischen Bindungen ⇒ Korrelation verwendet man
- die Kovarianz $\mu_{XY}$, die bei mittelwertfreien Komponenten gleich dem gemeinsamen linearen Moment erster Ordnung ist:
- $$\mu_{XY} = {\rm E}\big[X \cdot Y\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} X \cdot Y \cdot f_{XY}(x,y) \,{\rm d}x \, {\rm d}y ,$$
- den Korrelationskoeffizienten nach Normierung auf die beiden Effektivwerte $σ_X$ und $σ_Y$ der beiden Komponenten:
- $$\rho_{XY}=\frac{\mu_{XY} }{\sigma_X \cdot \sigma_Y}.$$
$\text{Eigenschaften des Korrelationskoeffizienten:}$
- Aufgrund der Normierung gilt stets $-1 \le ρ_{XY} ≤ +1$.
- Sind die beiden Zufallsgrößen $X$ und $Y$ unkorreliert, so ist $ρ_{XY} = 0$.
- Bei strenger linearer Abhängigkeit zwischen $X$ und $Y$ ist $ρ_{XY}= ±1$ ⇒ vollständige Korrelation.
- Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $X$–Wert im statistischen Mittel auch $Y$ größer ist als bei kleinerem $X$.
- Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $Y$ mit steigendem $X$ im Mittel kleiner wird.
Höhenlinien bei unkorrelierten Zufallsgrößen
Aus der Bedingungsgleichung $f_{XY}(x, y) = {\rm const.}$ können die Höhenlinien der WDF berechnet werden.
Sind die Komponenten $X$ und $Y$ unkorreliert $(ρ_{XY} = 0)$, so erhält man als Gleichung für die Höhenlinien:
- $$\frac{x^{\rm 2}}{\sigma_{X}^{\rm 2}}+\frac{y^{\rm 2}}{\sigma_{Y}^{\rm 2}} =\rm const.$$
Die Höhenlinien beschreiben in diesem Fall folgende Figuren:
- Kreise (falls $σ_X = σ_Y$, grüne Kurve), oder
- Ellipsen (für $σ_X ≠ σ_Y$, blaue Kurve) in Ausrichtung der beiden Achsen.
Korrelationsgerade
Als Korrelationsgerade bezeichnet man die Gerade $y = K(x)$ in der $(x, y)$–Ebene durch den „Mittelpunkt” $(m_X, m_Y)$. Diese besitzt folgende Eigenschaften:
- Die mittlere quadratische Abweichung von dieser Geraden – in $y$–Richtung betrachtet und über alle $N$ Messpunkte gemittelt – ist minimal:
- $$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$
- Die Korrelationsgerade kann als eine Art „statistische Symmetrieachse“ interpretiert werden. Die Geradengleichung lautet im allgemeinen Fall:
- $$y=K(x)=\frac{\sigma_Y}{\sigma_X}\cdot\rho_{XY}\cdot(x - m_X)+m_Y.$$
- Der Winkel, den die Korrelationsgerade zur $x$–Achse einnimmt, beträgt:
- $$\theta={\rm arctan}(\frac{\sigma_{Y} }{\sigma_{X} }\cdot \rho_{XY}).$$
Höhenlinien bei korrelierten Zufallsgrößen
Bei korrelierten Komponenten $(ρ_{XY} ≠ 0)$ sind die Höhenlinien der WDF (fast) immer elliptisch, also auch für den Sonderfall $σ_X = σ_Y$.
Ausnahme: $ρ_{XY}=\pm 1$ ⇒ Diracwand; siehe Aufgabe 4.4 im Buch „Stochastische Signaltheorie”, Teilaufgabe (5).
Hier lautet die Bestimmungsgleichung der WDF-Höhenlinien:
- $$f_{XY}(x, y) = {\rm const.} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \frac{x^{\rm 2} }{\sigma_{X}^{\rm 2}}+\frac{y^{\rm 2} }{\sigma_{Y}^{\rm 2} }-{\rm 2}\cdot\rho_{XY}\cdot\frac{x\cdot y}{\sigma_X\cdot \sigma_Y}={\rm const.}$$
Die Grafik zeigt in hellerem Blau für zwei unterschiedliche Parametersätze je eine Höhenlinie.
- Die Ellipsenhauptachse ist dunkelblau gestrichelt.
- Die Korrelationsgerade $K(x)$ ist durchgehend rot eingezeichnet.
Anhand dieser Darstellung sind folgende Aussagen möglich:
- Die Ellipsenform hängt außer vom Korrelationskoeffizienten $ρ_{XY}$ auch vom Verhältnis der beiden Streuungen $σ_X$ und $σ_Y$ ab.
- Der Neigungswinkel $α$ der Ellipsenhauptachse (gestrichelte Gerade) gegenüber der $x$–Achse hängt ebenfalls von $σ_X$, $σ_Y$ und $ρ_{XY}$ ab:
- $$\alpha = {1}/{2} \cdot {\rm arctan } \big ( 2 \cdot \rho_{XY} \cdot \frac {\sigma_X \cdot \sigma_Y}{\sigma_X^2 - \sigma_Y^2} \big ).$$
- Die (rote) Korrelationsgerade $y = K(x)$ einer Gaußschen 2D–Zufallsgröße liegt stets unterhalb der (blau gestrichelten) Ellipsenhauptachse.
- $K(x)$ kann aus dem Schnittpunkt der Höhenlinien und ihrer vertikalen Tangenten geometrisch konstruiert werden, wie in der Skizze in grüner Farbe angedeutet.
Zweidimensionale Verteilungsfunktion ⇒ 2D–VTF
$\text{Definition:}$ Die 2D-Verteilungsfunktion ist ebenso wie die 2D-WDF lediglich eine sinnvolle Erweiterung der eindimensionalen Verteilungsfunktion (VTF):
- $$F_{XY}(x,y) = {\rm Pr}\big [(X \le x) \cap (Y \le y) \big ] .$$
Es ergeben sich folgende Gemeinsamkeiten und Unterschiede zwischen der „1D-VTF” und der„ 2D-VTF”:
- Der Funktionalzusammenhang zwischen „2D–WDF” und „2D–VTF” ist wie im eindimensionalen Fall durch die Integration gegeben, aber nun in zwei Dimensionen. Bei kontinuierlichen Zufallsgrößen gilt:
- $$F_{XY}(x,y)=\int_{-\infty}^{y} \int_{-\infty}^{x} f_{XY}(\xi,\eta) \,\,{\rm d}\xi \,\, {\rm d}\eta .$$
- Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch partielle Differentiation nach $x$ und $y$ angeben:
- $$f_{XY}(x,y)=\frac{{\rm d}^{\rm 2} F_{XY}(\xi,\eta)}{{\rm d} \xi \,\, {\rm d} \eta}\Bigg|_{\left.{x=\xi \atop {y=\eta}}\right.}.$$
- Bezüglich der Verteilungsfunktion $F_{XY}(x, y)$ gelten folgende Grenzwerte:
- $$F_{XY}(-\infty,\ -\infty) = 0,\hspace{0.5cm}F_{XY}(x,\ +\infty)=F_{X}(x ),\hspace{0.5cm} F_{XY}(+\infty,\ y)=F_{Y}(y ) ,\hspace{0.5cm}F_{XY}(+\infty,\ +\infty) = 1.$$
- Im Grenzfall $($unendlich große $x$ und $y)$ ergibt sich demnach für die „2D-VTF” der Wert $1$. Daraus erhält man die Normierungsbedingung für die 2D-Wahrscheinlichkeitsdichtefunktion:
- $$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{XY}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$
$\text{Fazit:}$ Beachten Sie den signifikanten Unterschied zwischen eindimensionalen und zweidimensionalen Zufallsgrößen:
- Bei eindimensionalen Zufallsgrößen ergibt die Fläche unter der WDF stets den Wert $1$.
- Bei zweidimensionalen Zufallsgrößen ist das WDF-Volumen immer gleich $1$.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Bei der Aufgabenbeschreibung verwenden wir $\rho$ anstelle von $\rho_{XY}$.
- Für die „1D-WDF” gilt: $f_{X}(x) = \sqrt{1/(2\pi \cdot \sigma_X^2)} \cdot {\rm e}^{-x^2/(2 \hspace{0.05cm}\cdot \hspace{0.05cm} \sigma_X^2)}$.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
(1) Machen Sie sich anhand der Voreinstellung $(\sigma_X=1, \ \sigma_Y=0.5, \ \rho = 0.7)$ mit dem Programm vertraut. Interpretieren Sie die Grafiken für $\rm WDF$ und $\rm VTF$.
- $\rm WDF$ ist ein Bergrücken mit dem Maximum bei $x = 0, \ y = 0$. Der Bergkamm ist leicht verdreht gegenüber der $x$–Achse.
- $\rm VTF$ ergibt sich aus $\rm WDF$ durch fortlaufende Integration in beide Richtungen. Das Maximum $($nahezu $1)$ tritt bei $x=3, \ y=3$ auf.
(2) Nun lautet die Einstellung $\sigma_X= \sigma_Y=1, \ \rho = 0$. Welche Werte ergeben sich für $f_{XY}(0,\ 0)$ und $F_{XY}(0,\ 0)$? Interpretieren Sie die Ergebnisse.
- Das WDF–Maximum ist $f_{XY}(0,\ 0) = 1/(2\pi)= 0.1592$, wegen $\sigma_X= \sigma_Y = 1, \ \rho = 0$. Die Höhenlinien sind Kreise.
- Für den VTF-Wert gilt: $F_{XY}(0,\ 0) = [{\rm Pr}(X \le 0)] \cdot [{\rm Pr}(Y \le 0)] = 0.25$. Geringfügige Abweichung wegen numerischer Integration.
(3) Es gelten weiter die Einstellungen von (2). Welche Werte ergeben sich für $f_{XY}(0,\ 1)$ und $F_{XY}(0,\ 1)$? Interpretieren Sie die Ergebnisse.
- Es gilt $f_{XY}(0,\ 1) = f_{X}(0) \cdot f_{Y}(1) = [ \sqrt{1/(2\pi)}] \cdot [\sqrt{1/(2\pi)} \cdot {\rm e}^{-0.5}] = 1/(2\pi) \cdot {\rm e}^{-0.5} = 0.0965$.
- Das Programm liefert $F_{XY}(0,\ 1) = [{\rm Pr}(X \le 0)] \cdot [{\rm Pr}(Y \le 1)] = 0.4187$, also einen größeren Wert als in (2), da weiter integriert wird.
(4) Die Einstellungen bleiben erhalten. Welche Werte ergeben sich für $f_{XY}(1,\ 0)$ und $F_{XY}(1,\ 0)$? Interpretieren Sie die Ergebnisse.
- Aufgrund der Rotationssysmmetrie gleiche Ergebnisse wie in (3).
(5) Stimmt die Aussage: „Elliptische Höhenlinien gibt es nur für $\rho \ne 0$”. Interpretieren Sie die $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ und $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ für $\sigma_X=1, \ \sigma_Y=0.5$ und $\rho = 0$.
- Nein! Auch für $\ \rho = 0$ sind die Höhenlinien elliptisch (nicht kreisförmig), falls $\sigma_X \ne \sigma_Y$.
- Für $\sigma_X \gg \sigma_Y$ hat die $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ die Form eines langgestreckten Bergkamms parallel zur $x$–Achse, für $\sigma_X \ll \sigma_Y$ parallel zur $y$–Achse.
- Für $\sigma_X \gg \sigma_Y$ ist der Anstieg der $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ in Richtung der $y$–Achse deutlich steiler als in Richtung der $x$–Achse.
(6) Variieren Sie ausgehend von $\sigma_X=\sigma_Y=1, \ \rho = 0.7$ den Korrelationskoeffizienten $\rho$. Wie groß ist der Neigungswinkel $\alpha$ der Ellipsen–Hauptachse?
- Für $\rho > 0$ ist $\alpha = 45^\circ$ und für $\rho < 0$ ist $\alpha = -45^\circ$. Für $\rho = 0$ sind die Höhenlinien kreisfömig und somit gibt es auch keine Ellipsen–Hauptachse.
(7) Variieren Sie ausgehend von $\sigma_X=\sigma_Y=1, \ \rho = 0.7$ den Korrelationskoeffizienten $\rho > 0$. Wie groß ist der Neigungswinkel $\theta$ der Korrelationsgeraden $K(x)$?
- Für $\sigma_X=\sigma_Y$ ist $\theta={\rm arctan}\ (\rho)$. Die Steigung nimmt mit wachsendem $\rho > 0$ zu. In allen Fällen gilt $\theta < \alpha = 45^\circ$. Für $\rho = 0.7$ ergibt sich $\theta = 35^\circ$.
(8) Variieren Sie ausgehend von $\sigma_X=\sigma_Y=0.75, \ \rho = 0.7$ die Parameter $\sigma_Y$ und $\rho \ (>0)$. Welche Aussagen gelten für die Winkel $\alpha$ und $\theta$?
- Für $\sigma_Y<\sigma_X$ ist $\alpha < 45^\circ$ und für $\sigma_Y>\sigma_X$ dagegen $\alpha > 45^\circ$.
- Bei allen Einstellungen gilt: Die Korrelationsgerade liegt unter der Ellipsen–Hauptachse.
(9) Gehen Sie von $\sigma_X= 1, \ \sigma_Y=0.75, \ \rho = 0.7$ aus und variieren Sie $\rho$. Wie könnte man die Korrelationsgerade aus den Höhenlinien konstruieren?
- Die Korrelationsgerade schneidet alle Höhenlinien an den Punkten, an denen die Tangente zu der Höhenlinie senkrecht verläuft.
(10) Nun gelte $\sigma_X= \sigma_Y=1, \ \rho = 0.95$. Interpretieren Sie die $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$. Welche Aussagen würden für den Grenzfall $\rho \to 1$ zutreffen?
- Die $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ hat nur Anteile in der Nähe der Ellipsen–Hauptachse. Die Korrelationsgerade liegt nur knapp darunter: $\alpha = 45^\circ, \ \theta = 43.5^\circ$.
- Im Grenzfall $\rho \to 1$ wäre $\theta = \alpha = 45^\circ$. Außerhalb der Korrelationsgeraden hätte die $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ keine Anteile. Das heißt:
- Längs der Korrelationsgeraden ergäbe sich eine Diracwand ⇒ Alle Werte sind unendlich groß, trotzdem um den Mittelwert gaußisch gewichtet.
Zur Handhabung des Applets
(A) Parametereingabe per Slider: $\sigma_X$, $\sigma_Y$ und $\rho$
(B) Auswahl: Darstellung von WDF oder VTF
(C) Reset: Einstellung wie beim Programmstart
(D) Höhenlinien darstellen anstelle von „1D-WDF”
(E) Darstellungsbereich für „2D-WDF”
(F) Manipulation der 3D-Grafik (Zoom, Drehen, ...)
(G) Darstellungsbereich für „1D-WDF” bzw. „Höhenlinien”
(H) Manipulation der 2D-Grafik („1D-WDF”)
( I ) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(J) Bereich für die Versuchsdurchführung: Aufgabenstellung
( L) Bereich für die Versuchsdurchführung: Musterlösung
Werte–Ausgabe über Maussteuerung (sowohl bei 2D als auch bei 3D)
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.