Aufgaben:Aufgabe 5.1: Gaußsche AKF und Gaußtiefpass

• Zurück zum Buch

Gaußsche AKF am
Eingang und Ausgang

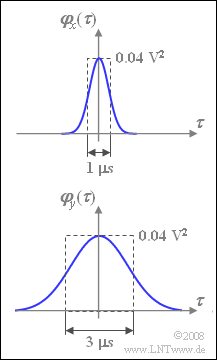
Am Eingang eines Tiefpassfilters mit dem Frequenzgang  $H(f)$  liegt ein gaußverteiltes mittelwertfreies Rauschsignal  $x(t)$  mit folgender Autokorrelationsfunktion (AKF) an:

$${\it \varphi}_{x}(\tau) = \sigma_x^2 \cdot {\rm e}^{- \pi (\tau /{\rm \nabla} \tau_x)^2}.$$

Diese AKF ist in nebenstehender Grafik oben dargestellt.

Das Filter sei gaußförmig mit der Gleichsignalverstärkung  $H_0$  und der äquivalenten Bandbreite  $\Delta f$.  Für den Frequenzgang kann somit geschrieben werden:

$$H(f) = H_{\rm 0} \cdot{\rm e}^{- \pi (f/ {\rm \Delta} f)^2}.$$

Im Verlaufe dieser Aufgabe sollen die beiden Filterparameter  $H_0$  und  $\Delta f$  so dimensioniert werden, dass das Ausgangssignal  $y(t)$  eine AKF entsprechend der unteren Skizze aufweist.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Stochastische Systemtheorie.
• Bezug genommen wird auch auf das Kapitel  Autokorrelationsfunktion.

• Berücksichtigen Sie die folgende Fourierkorrespondenz:

$${\rm e}^{- \pi (f/{\rm \Delta} f)^2} \hspace{0.15cm} \bullet\!\!-\!\!\!-\!\!\!\hspace{0.03cm}\circ \hspace{0.15cm}{\rm \Delta} f \cdot {\rm e}^{- \pi ({\rm \Delta} f \hspace{0.03cm} \cdot \hspace{0.03cm} t)^2}.$$

Fragebogen

1

Wie groß ist der Effektivwert des Filtereingangssignals?

$\sigma_x \ = \ $ $\ \rm V$

2

Bestimmen Sie aus der skizzierten AKF auch die äquivalente AKF-Dauer  $\nabla\tau_x$  des Signals  $x(t)$.  Wie kann diese allgemein ermittelt werden?

$\nabla\tau_x \ = \ $ $\ µ s$

3

Wie lautet das Leistungsdichtespektrum  ${\it Φ}_x(f)$ des Eingangsignals?  Wie groß ist der LDS-Wert bei $f= 0$?

${\it Φ}_x(f=0) \ = \ $ $\ \cdot 10^{-9}\ \rm V^2/Hz$

4

Berechnen Sie das LDS  ${\it Φ}_y(f)$  am Filterausgang allgemein als Funktion von  $\sigma_x$,  $\nabla \tau_x$,  $H_0$  und  $\Delta f$.  Welche Aussagen treffen zu?

	Das LDS  ${\it Φ}_y(f)$  ist ebenfalls gaußförmig.
	Je kleiner  $\Delta f$  ist, um so breiter ist  ${\it Φ}_y(f)$.
	$H_0$  beeinflusst nur die Höhe, aber nicht die Breite von  ${\it Φ}_y(f)$.

5

Wie groß muss die äquivalente Filterbandbreite  $\Delta f$  gewählt werden, damit für die äquivalente AKF-Dauer  $\nabla \tau_y = 3 \ \rm µ s$  gilt?

$\Delta f \ = \ $ $\ \rm MHz$

6

Wie groß muss man den Gleichsignalübertragungsfaktor  $H_0$  wählen, damit die Bedingung  $\sigma_y = \sigma_x$  erfüllt wird?

$H_0 \ = \ $

Musterlösung

Musterlösung

(1)  Die Varianz ist gleich dem AKF-Wert bei  $\tau = 0$, also  $\sigma_x^2 = 0.04 \ \rm V^2$.

• Daraus folgt  $\sigma_x\hspace{0.15cm}\underline {= 0.2 \ \rm V}$ .

(2)  Die äquivalente AKF-Dauer kann man über das flächengleiche Rechteck ermitteln.

• Gemäß der Skizze erhält man  $\nabla \tau_x\hspace{0.15cm}\underline {= 1 \ \rm µ s}$.

(3)  Das LDS ist die Fouriertransformierte der AKF.

• Mit der gegebenen Fourierkorrespondenz gilt:

$${\it \Phi}_{x}(f) = \sigma_x^2 \cdot {\rm \nabla} \tau_x \cdot {\rm e}^{- \pi ({\rm \nabla} \tau_x \hspace{0.03cm}\cdot \hspace{0.03cm}f)^2} .$$

• Bei der Frequenz $f = 0$  erhält man:

$${\it \Phi}_{x}(f = 0) = \sigma_x^2 \cdot {\rm \nabla} \tau_x = \rm 0.04 \hspace{0.1cm} V^2 \cdot 10^{-6} \hspace{0.1cm} s \hspace{0.15cm} \underline{= 40 \cdot 10^{-9} \hspace{0.1cm} V^2 / Hz}.$$

(4)  Richtig sind die Lösungsvorschläge 1 und 3:

• Allgemein gilt  ${\it \Phi}_{y}(f) = {\it \Phi}_{x}(f) \cdot |H(f)|^2$.  Daraus folgt:

$${\it \Phi}_{y}(f) = \sigma_x^2 \cdot {\rm \nabla} \tau_x \cdot {\rm e}^{- \pi ({\rm \nabla} \tau_x \cdot f)^2}\cdot H_{\rm 0}^2 \cdot{\rm e}^{- 2 \pi (f/ {\rm \Delta} f)^2} .$$

• Durch Zusammenfassen der beiden Exponentialfunktionen erhält man:

$${\it \Phi}_{y}(f) = \sigma_x^2 \cdot {\rm \nabla} \tau_x \cdot H_0^2 \cdot {\rm e}^{- \pi\cdot ({\rm \nabla} \tau_x^2 + 2/\Delta f^2 ) \hspace{0.1cm}\cdot f^2}.$$

• Auch ${\it \Phi}_{y}(f)$  ist gaußförmig und nie breiter als  ${\it \Phi}_{x}(f)$.  Für $f \to \infty$  gilt die Näherung  ${\it \Phi}_{y}(f) \approx {\it \Phi}_{x}(f)$.
• Mit kleiner werdendem  $\Delta f$  wird  ${\it \Phi}_{y}(f)$  immer schmäler  (also ist die zweite Aussage falsch).
• $H_0$  beeinflusst tatsächlich nur die LDS-Höhe, aber nicht die Breite des LDS.

(5)  Analog zum Aufgabenteil  (1)  kann für das LDS des Ausgangssignals  $y(t)$  geschrieben werden:

$${\it \Phi}_{y}(f) = \sigma_y^2 \cdot {\rm \nabla} \tau_y \cdot {\rm e}^{- \pi \cdot {\rm \nabla} \tau_y^2 \cdot f^2 }.$$

• Durch Vergleich mit dem Ergebnis aus  (4)  ergibt sich:

$${{\rm \nabla} \tau_y^2} = {{\rm \nabla} \tau_x^2} + \frac {2}{{\rm \Delta} f^2}.$$

• Löst man die Gleichung nach  $\Delta f$  auf und berücksichtigt die Werte  $\nabla \tau_x {= 1 \ \rm µ s}$  sowie  $\nabla \tau_y {= 3 \ \rm µ s}$, so folgt:

$${\rm \Delta} f = \sqrt{\frac{2}{{\rm \nabla} \tau_y^2 - {\rm \nabla} \tau_x^2}} = \sqrt{\frac{2}{9 - 1}} \hspace{0.1cm}\rm MHz \hspace{0.15cm} \underline{= 0.5\hspace{0.1cm} MHz} .$$

(6)  Die Bedingung  $\sigma_y = \sigma_x$  ist gleichbedeutend mit  $\varphi_y(\tau = 0)= \varphi_x(\tau = 0)$.

• Da zudem  $\nabla \tau_y = 3 \cdot \nabla \tau_x$  vorgegeben ist, muss deshalb auch  ${\it \Phi}_{y}(f= 0) = 3 \cdot {\it \Phi}_{x}(f= 0)$  gelten.
• Daraus erhält man:

$$H_{\rm 0} = \sqrt{\frac{\it \Phi_y (f \rm = 0)}{\it \Phi_x (f = \rm 0)}} = \sqrt {3}\hspace{0.15cm} \underline{=1.732}.$$