Aufgaben:Aufgabe 4.8Z: Was sagt die AWGN-Kanalkapazitätskurve aus?

• Zurück zum Buch

AWGN–Kanalkapazität als Funktion von  $10 \cdot \lg (E_{\rm B}/{N_0})$

Wir betrachten wie in  Aufgabe 4.8  die Kanalkapazität des AWGN–Kanals:

$$C_{\rm Gauß}( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) . $$

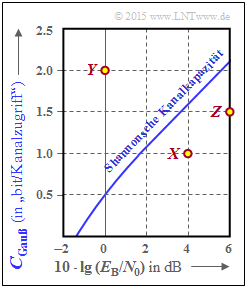
• Die Kurve ist rechts bei logarithmischer Abszisse zwischen  $-2 \ \rm dB$ und $+6 \ \rm dB$  dargestellt.
• Der Zusatz „Gauß” weist darauf hin, dass für diese Kurve am AWGN–Eingang eine Gaußverteilung vorausgesetzt wurde.

Eingezeichnet sind in obiger Grafik durch Punkte drei Systemvarianten:

• System $X$:    mit  $10 \cdot \lg (E_{\rm B}/{N_0}) = 4 \ \rm dB$  und  $R = 1$,
• System $Y$:    mit  $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$  und  $R = 2$,
• System $Z$:    mit  $10 \cdot \lg (E_{\rm B}/{N_0}) = 6 \ \rm dB$  und  $R = 1.5$.

In den Fragen zu dieser Aufgabe verwenden wir noch folgende Begriffe:

• Digitalsystem:   Symbolumfang  $M_X = |X|$  beliebig,
• Binärsystem:   Symbolumfang  $M_X = 2$,
• Quaternärsystem:   Symbolumfang  $M_X = 4$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
• Bezug genommen wird insbesondere auf die Seite  Die Kanalkapazität $C$ als Funktion von $E_{\rm B}/{N_0}$.
• Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log”   ⇒   „log₂” verwendet.

Fragebogen

1

Welche Aussage liefert der Punkt  $X$  für die Digitalsignalübertragung?

	Für  $10 \cdot \lg (E_{\rm B}/{N_0}) = 4 \ \rm dB$  ist ein Digitalsystem mit der Rate  $R = 1$  und der Fehlerwahrscheinlichkeit Null vorstellbar.
	Ein solches System kommt ohne Kanalcodierung aus.
	Ein solches System verwendet einen unendlich langen Code.
	Auch ein Binärsystem kann die Voraussetzungen erfüllen.

2

Welche Aussage liefert der Punkt  $Y$  für die Digitalsignalübertragung?

	Für  $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$  ist ein Digitalsystem mit der Rate  $R = 2$  und der Fehlerwahrscheinlichkeit Null vorstellbar.
	Für  $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$  wäre  $R = 0.5$  ausreichend.
	Für die Rate  $R = 2$  würde  $10 \cdot \lg (E_{\rm B}/{N_0}) = 5 \ \rm dB$  genügen.

3

Welche Aussage liefert der Punkt  $Z$  für die Binärübertragung?

	Ein Binärsystem erfüllt die Anforderungen auf keinen Fall.
	Die Kurve  $C_\text{Gauß}(E_{\rm B}/{N_0})$  reicht für diese Bewertung nicht aus.

4

Welche Aussage liefert der Punkt  $Z$  für die Quaternärübertragung?

	Ein Quaternärsystem erfüllt die Anforderungen auf keinen Fall.
	Die Kurve  $C_\text{Gauß}(E_{\rm B}/{N_0})$  reicht für diese Bewertung nicht aus.

Musterlösung

Musterlösung

(1)  Richtig sind die Lösungsvorschläge 1 und 3:

• Da der Punkt  $X$  rechts von der Kanalkapazitätskurve  $C_\text{Gauß}(E_{\rm B}/{N_0})$  liegt, gibt es (mindestens) ein Nachrichtensystem der Rate  $R = 1$, das mit  $10 \cdot \lg (E_{\rm B}/{N_0}) = 4 \ \rm dB$  eine quasi–fehlerfreie Übertragung ermöglicht.
• Trotz der Coderate  $R = 1$  beinhaltet dieses System eine Kanalcodierung mit einem unendlich langen Code, der aber leider unbekannt ist.
• Ein Binärsystem der Rate  $R = 1$  erlaubt allerdings keine Kanalcodierung.

(2)  Richtig ist nur der Lösungsvorschlag 2. Hier gelten folgende Aussagen:

• Das erforderliche  $E_{\rm B}/{N_0}$  für die Rate  $R = 2$  ergibt sich zu

$$(E_{\rm B}/{N_0})_{\rm min} = \frac{2^{2R} - 1} { 2 \cdot R} = \frac{2^4 - 1} { 4 } = 3.75 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0})_{\rm min} = 15.74\,{\rm dB} \hspace{0.05cm}. $$

• Die maximale Coderate  $R_{\rm max}$  für  $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$    ⇒   $E_{\rm B}/{N_0} = 1$  berechnet sich wie folgt:

$$C = R = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 2^{2R} - 1 \stackrel{!}{=} 2 R \hspace{0.3cm}\Rightarrow \hspace{0.3cm} R_{\rm max} = 0.5 \hspace{0.05cm}. $$

• Beide Berechnungen zeigen, dass der Punkt  $Y$  mit den Kenngrößen  $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$  und  $R = 1$  das Kanalcodierungstheorem nicht erfüllt.

(3)  Mit einem Binärsystem ist die Rate  $R = 1.5$  niemals realisierbar  ⇒   Lösungsvorschlag 1.

(4)  Richtig ist der Lösungsvorschlag 2:

• Der Punkt  $Z$  liegt rechts von der Grenzkurve und für die Coderate eines Quaternärsystems gilt  $R \le 2$. 
• Die Rate  $R =1.5$  wäre also mit  $M_X = 4$  durchaus zu realisieren.
• Der Lösungsvorschlag 1 ist falsch. Richtig ist dagegen der zweite Lösungsvorschlag:

• Die vorgegebene Kurve  $C_\text{Gauß}(E_{\rm B}/{N_0})$  geht stets von einem gaußverteilten Eingang aus.
• Für ein Binärsystem ergibt sich eine andere Grenzkurve, nämlich  $C_\text{BPSK} ≤ 1 \ \rm bit/Kanalzugriff$. $C_\text{Gauß}$  und  $C_\text{BPSK}$  unterscheiden sich signifikant.
• Für das Quaternärsystem  $(M_X = 4)$  müsste man die Kurve  $C_{M=4}$  berechnen und analysieren.  Auch hier gilt  $C_{M=4} ≤ C_\text{Gauß}$ .
• Für kleines  $E_{\rm B}/{N_0}$  gilt  $C_{M=4} \approx C_\text{Gauß}$, danach weicht der Kurvenverlauf deutlich ab und endet in einer Horizontalen bei  $C_{M=4} = 2 \ \rm bit/Kanalzugriff$.

Der Punkt  $Z$    ⇒   $10 \cdot \lg (E_{\rm B}/{N_0}) = 6 \ \rm dB, \ \ R = 1.5$  liegt unterhalb von  $C_{M=4}$.

• Ein solches Quaternärsystem wäre also realisierbar, wie in der  Aufgabe 4.10  noch gezeigt wird.
• Aber allein aus Kenntnis von  $C_\text{Gauß}$  kann die Frage nicht beantwortet werden (Lösungsvorschlag 2).