Aufgaben:Aufgabe 1.3: Systemvergleich beim AWGN–Kanal: Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
[[Datei:P_ID960__Mod_A_1_3.png|right|frame|Systemvergleich beim AWGN–Kanal]] | [[Datei:P_ID960__Mod_A_1_3.png|right|frame|Systemvergleich beim AWGN–Kanal]] | ||
Für den Vergleich verschiedener Modulationsverfahren und Demodulatoren hinsichtlich der Rauschempfindlichkeit gehen wir meist vom so genannten [[Modulationsverfahren/Qualitätskriterien#Einige_Anmerkungen_zum_AWGN.E2.80.93Kanalmodell|AWGN–Kanal]] aus und beschreiben folgendes doppelt–logarithmische Diagramm: | Für den Vergleich verschiedener Modulationsverfahren und Demodulatoren hinsichtlich der Rauschempfindlichkeit gehen wir meist vom so genannten [[Modulationsverfahren/Qualitätskriterien#Einige_Anmerkungen_zum_AWGN.E2.80.93Kanalmodell|AWGN–Kanal]] aus und beschreiben folgendes doppelt–logarithmische Diagramm: | ||
| − | *Die Ordinate gibt den Sinken–Störabstand (SNR logarithmiert) $10 · \lg ρ_v$ in dB an. | + | *Die Ordinate gibt den Sinken–Störabstand $\rm (SNR$, logarithmiert$)$ $10 · \lg ρ_v$ in dB an. |
| − | *Auf der Abszisse ist $10 · \lg ξ$ aufgetragen; für die normierte Leistungskenngröße gilt: | + | *Auf der Abszisse ist $10 · \lg ξ$ aufgetragen; für die normierte Leistungskenngröße gilt: |
:$$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$ | :$$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$ | ||
| − | *In $ξ$ sind also die Sendeleistung $P_{\rm S}$, der Kanaldämpfungsfaktor $α_{\rm K}$, die Rauschleistungsdichte $N_0$ sowie die Bandbreite $B_{\rm NF}$ des Nachrichtensignals in geeigneter Weise zusammengefasst. | + | *In $ξ$ sind also die Sendeleistung $P_{\rm S}$, der Kanaldämpfungsfaktor $α_{\rm K}$, die Rauschleistungsdichte $N_0$ sowie die Bandbreite $B_{\rm NF}$ des Nachrichtensignals in geeigneter Weise zusammengefasst. |
* Wenn nicht ausdrücklich etwas anderes angegeben ist, soll in der Aufgabe von folgenden Werten ausgegangen werden: | * Wenn nicht ausdrücklich etwas anderes angegeben ist, soll in der Aufgabe von folgenden Werten ausgegangen werden: | ||
:$$P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm | :$$P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm | ||
| Zeile 15: | Zeile 15: | ||
B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$ | B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$ | ||
| − | In der Grafik sind zwei Systeme eingezeichnet, deren $(x, y)$–Verlauf wie folgt beschrieben werden kann: | + | In der Grafik sind zwei Systeme eingezeichnet, deren $(x, y)$–Verlauf wie folgt beschrieben werden kann: |
*Das $\text{System A}$ ist gekennzeichnet durch die folgende Gleichung: | *Das $\text{System A}$ ist gekennzeichnet durch die folgende Gleichung: | ||
:$$y = x+1.$$ | :$$y = x+1.$$ | ||
| Zeile 22: | Zeile 22: | ||
Die in der Grafik zusätzlich grün eingezeichneten Achsenbeschriftungen haben folgende Bedeutung: | Die in der Grafik zusätzlich grün eingezeichneten Achsenbeschriftungen haben folgende Bedeutung: | ||
:$$ x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$ | :$$ x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$ | ||
| − | So steht $x = 4$ für $10 · \lg ξ = 40\text{ dB}$ bzw. $ξ = 10^4$ und $y = 5$ steht für $10 · \lg ρ_v= 50\text{ dB}$ , also $ρ_v = 10^5$. | + | So steht $x = 4$ für $10 · \lg ξ = 40\text{ dB}$ bzw. $ξ = 10^4$ und $y = 5$ steht für $10 · \lg ρ_v= 50\text{ dB}$ , also $ρ_v = 10^5$. |
| Zeile 29: | Zeile 29: | ||
| − | + | Hinweise: | |
| − | |||
| − | |||
| − | |||
*Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Qualitätskriterien|Qualitätskriterien]]. | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Qualitätskriterien|Qualitätskriterien]]. | ||
*Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Qualitätskriterien#Untersuchungen_beim_AWGN.E2.80.93Kanal|Untersuchungen beim AWGN-Kanal]]. | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Qualitätskriterien#Untersuchungen_beim_AWGN.E2.80.93Kanal|Untersuchungen beim AWGN-Kanal]]. | ||
| Zeile 47: | Zeile 44: | ||
$10 · \lg \hspace{0.05cm}ρ_v \ = \ $ { 50 3% } $\ \text{dB}$ | $10 · \lg \hspace{0.05cm}ρ_v \ = \ $ { 50 3% } $\ \text{dB}$ | ||
| − | {Es wird nun $10 · \lg \hspace{0.05cm} ρ_v ≥ 60\text{ dB}$ gefordert. Durch welche Maßnahmen (jeweils für sich allein) ist dies zu erreichen? | + | {Es wird nun $10 · \lg \hspace{0.05cm} ρ_v ≥ 60\text{ dB}$ gefordert. Durch welche Maßnahmen (jeweils für sich allein) ist dies zu erreichen? |
|type="[]"} | |type="[]"} | ||
- Erhöhung der Sendeleistung von $P_{\rm S}= 5\text{ kW}$ auf $10\text{ kW}$ . | - Erhöhung der Sendeleistung von $P_{\rm S}= 5\text{ kW}$ auf $10\text{ kW}$ . | ||
+ Erhöhung des Kanalübertragungsfaktors von $α_{\rm K} = 0.001$ auf $0.004$. | + Erhöhung des Kanalübertragungsfaktors von $α_{\rm K} = 0.001$ auf $0.004$. | ||
+ Reduzierung der Rauschleistungsdichte auf $N_0=10^{–11 }\text{ W/Hz}$. | + Reduzierung der Rauschleistungsdichte auf $N_0=10^{–11 }\text{ W/Hz}$. | ||
| − | - Erhöhung der NF–Bandbreite von $B_{\rm NF}= 5\text{ kHz}$ auf $\text{ kHz}$. | + | - Erhöhung der NF–Bandbreite von $B_{\rm NF}= 5\text{ kHz}$ auf $10\text{ kHz}$. |
{Welcher Störabstand ergibt sich bei $\text{System B}$ mit $10 · \lg ξ = 40\text{ dB}$? | {Welcher Störabstand ergibt sich bei $\text{System B}$ mit $10 · \lg ξ = 40\text{ dB}$? | ||
| Zeile 58: | Zeile 55: | ||
$10 · \lg \hspace{0.05cm}ρ_v \ = \ $ { 57 3% } $\ \text{dB}$ | $10 · \lg \hspace{0.05cm}ρ_v \ = \ $ { 57 3% } $\ \text{dB}$ | ||
| − | {Gefordert wird der Störabstand $10 · \lg ρ_v = 50\text{ dB}$. Welche Sendeleistung $P_{\rm S}$ genügt bei $\text{System B}$, um diese Qualität zu erzielen? | + | {Gefordert wird der Störabstand $10 · \lg ρ_v = 50\text{ dB}$. Welche Sendeleistung $P_{\rm S}$ genügt bei $\text{System B}$, um diese Qualität zu erzielen? |
|type="{}"} | |type="{}"} | ||
$P_{\rm S} \ = \ $ { 0.3 3% } $\ \text{ kW }$ | $P_{\rm S} \ = \ $ { 0.3 3% } $\ \text{ kW }$ | ||
Version vom 16. November 2021, 12:21 Uhr
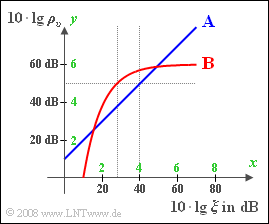
Für den Vergleich verschiedener Modulationsverfahren und Demodulatoren hinsichtlich der Rauschempfindlichkeit gehen wir meist vom so genannten AWGN–Kanal aus und beschreiben folgendes doppelt–logarithmische Diagramm:
- Die Ordinate gibt den Sinken–Störabstand $\rm (SNR$, logarithmiert$)$ $10 · \lg ρ_v$ in dB an.
- Auf der Abszisse ist $10 · \lg ξ$ aufgetragen; für die normierte Leistungskenngröße gilt:
- $$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$
- In $ξ$ sind also die Sendeleistung $P_{\rm S}$, der Kanaldämpfungsfaktor $α_{\rm K}$, die Rauschleistungsdichte $N_0$ sowie die Bandbreite $B_{\rm NF}$ des Nachrichtensignals in geeigneter Weise zusammengefasst.
- Wenn nicht ausdrücklich etwas anderes angegeben ist, soll in der Aufgabe von folgenden Werten ausgegangen werden:
- $$P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm K} = 0.001\hspace{0.05cm}, \hspace{0.2cm} {N_0} = 10^{-10}\;{\rm W}/{\rm Hz}\hspace{0.05cm}, \hspace{0.2cm} B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$
In der Grafik sind zwei Systeme eingezeichnet, deren $(x, y)$–Verlauf wie folgt beschrieben werden kann:
- Das $\text{System A}$ ist gekennzeichnet durch die folgende Gleichung:
- $$y = x+1.$$
- Entsprechend gilt für das $\text{System B}$:
- $$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right)\hspace{0.05cm}.$$
Die in der Grafik zusätzlich grün eingezeichneten Achsenbeschriftungen haben folgende Bedeutung:
- $$ x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$
So steht $x = 4$ für $10 · \lg ξ = 40\text{ dB}$ bzw. $ξ = 10^4$ und $y = 5$ steht für $10 · \lg ρ_v= 50\text{ dB}$ , also $ρ_v = 10^5$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Qualitätskriterien.
- Bezug genommen wird insbesondere auf die Seite Untersuchungen beim AWGN-Kanal.
- Durch die Angabe der Leistungen in $\rm W$att sind diese unabhängig vom Bezugswiderstand $R$.
Fragebogen
Musterlösung
- $$\xi = \frac{5 \cdot 10^3\,{\rm W}\cdot 10^{-6} }{10^{-10}\,{\rm W}/{\rm Hz} \cdot 5 \cdot 10^3\,{\rm Hz}} = 10^4 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = 40\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x=4 \hspace{0.05cm}.$$
- Damit ergibt sich der Hilfsordinatenwert $y = 5$, was zum Sinken-Störabstand $10 · \lg \hspace{0.05cm} ρ_v\hspace{0.15cm}\underline{ = 50 \ \rm dB}$ führt.
(2) Richtig sind die Alternativen 2 und 3:
Diese Forderung entspricht gegenüber dem bisherigen System einer Erhöhung des Störabstandes um $10$ dB, so dass auch $10 · \lg \hspace{0.05cm}ξ$ um $10$ dB erhöht werden muss:
- $$10 \cdot {\rm lg} \hspace{0.1cm}\xi = 50\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \xi=10^5 \hspace{0.05cm}.$$
Ein $10$–fach größerer $ξ$–Wert wird erreicht – vorausgesetzt die anderen Parameter bleiben jeweils gleich:
- durch die Sendeleistung $P_{\rm S} = 50$ kW statt $5$ kW,
- durch den Kanalübertragungsfaktor $α_{\rm K} = 0.00316$ anstelle von $0.001$,
- durch die Rauschleistungsdichte $N_0 = 10^{ –11 }$ W/Hz statt $10^{ –10 }$ W/Hz,
- durch die Bandbreite $B_{\rm NF} = 0.5$ kHz statt $5$ kHz.
(3) Für $10 · \lg \hspace{0.05cm} ξ = 40$ dB ist die Hilfsgröße $x = 4$. Damit ergibt sich für die Hilfsgröße der Ordinate:
- $$y= 6 \cdot \left(1 - {\rm e}^{-3} \right)\approx 5.7 \hspace{0.05cm}.$$
- Dies entspricht dem Sinken–Störabstand $10 · \lg \hspace{0.05cm} ρ_v\hspace{0.15cm}\underline{ = 57 \ \rm dB}$, also einer Verbesserung gegenüber dem $\text{System A}$ um $7$ dB.
(4) Diese Problemstellung wird durch folgende Gleichung beschrieben:
- $$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right) = 5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm e}^{-x+1} ={1}/{6}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} x = 1+ {\rm ln} \hspace{0.1cm}6 \approx 2.79 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = 27.9\,{\rm dB}\hspace{0.05cm}.$$
- Bei $\text{System A}$ war hierfür $10 · \lg \hspace{0.05cm} \xi = 40$ dB notwendig, was bei den weiter gegebenen Zahlenwerten durch $P_{\rm S} = 5$ kW erreicht wurde.
- Nun kann die Sendeleistung um etwa $12.1$ dB verringert werden:
- $$ 10 \cdot {\rm lg} \hspace{0.1cm} \frac{P_{\rm S}}{ 5 \;{\rm kW}}= -12.1\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{P_{\rm S}}{ 5 \;{\rm kW}} = 10^{-1.21}\approx 0.06\hspace{0.05cm}.$$
- Das bedeutet: Bei $\text{System B}$ wird mit nur $6\%$ der Sendeleistung von $\text{System A}$ – also mit nur $P_{\rm S} \hspace{0.15cm}\underline{ = 0.3 \ \rm kW}$ – die gleiche Systemqualität erzielt.
(5) Wir bezeichnen mit $V$ (steht für „Verbesserung”) den größeren Sinken–Störabstand von $\text{System B}$ gegenüber $\text{System A}$ :
- $$V = 10 \cdot {\rm lg} \hspace{0.1cm}\rho_v \hspace{0.1cm}{\rm (System\;B)} - 10 \cdot {\rm lg} \hspace{0.1cm}\rho_v \hspace{0.1cm}{\rm (System\;A)} = \left[6 \cdot \left(1 - {\rm e}^{-x+1} \right) -x -1 \right] \cdot 10\,{\rm dB}\hspace{0.05cm}.$$
- Durch Nullsetzen der Ableitung ergibt sich derjenige $x$–Wert, der zur maximalen Verbesserung führt:
- $$ \frac{{\rm d}V}{{\rm d}x} = 6 \cdot {\rm e}^{-x+1} -1\Rightarrow \hspace{0.3cm} x = 1+ {\rm ln} \hspace{0.1cm}6 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = \hspace{0.15cm}\underline {27.9\,{\rm dB}}\hspace{0.05cm}.$$
- Es ergibt sich also genau der in der Teilaufgabe (4) behandelte Fall mit $10 · \lg ρ_υ = 50$ dB, während der Störabstand bei $\text{System A}$ nur $37.9$ dB beträgt.
- Die Verbesserung ist demnach $12.1$ dB.