Aufgaben:Aufgabe 4.7: Kupfer-Doppelader 0.5 mm: Unterschied zwischen den Versionen
| Zeile 90: | Zeile 90: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Mit $ | + | '''(1)''' Mit ${\rm a}_0 = \alpha_0 \cdot l \approx 0.76 \ \rm Np$ erhält man für die Konstante $K$, die den Einfluss des Koeffizienten $ \alpha_0$ auf die Impulsantwort angibt: |
| − | :$$K = {\rm e}^{-{a}_0 }= {\rm e}^{-0.76} \hspace{0.15cm}\underline{= 0.468} \hspace{0.05cm}.$$ | + | :$$K = {\rm e}^{-{\rm a}_0 }= {\rm e}^{-0.76} \hspace{0.15cm}\underline{= 0.468} \hspace{0.05cm}.$$ |
| Zeile 103: | Zeile 103: | ||
| − | '''(3)''' Die Impulsantwort eines Koaxialkabels ist näherungsweise gleich $h_2(t)$, wenn das Kabel folgende charakteristische Kabeldämpfung aufweist: | + | '''(3)''' Die Impulsantwort eines Koaxialkabels ist näherungsweise gleich $h_2(t)$, wenn das Kabel folgende charakteristische Kabeldämpfung aufweist: |
| − | :$${a}_\star ={a}_2 = \alpha_2 \cdot l \cdot \sqrt{{R}/{2}} = | + | :$${\rm a}_\star ={\rm a}_2 = \alpha_2 \cdot l \cdot \sqrt{{R}/{2}} = |
1.1467\,\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}} \cdot 1.5\,{\rm km} \cdot \sqrt{\frac{10\,{\rm MHz}}{2}} | 1.1467\,\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}} \cdot 1.5\,{\rm km} \cdot \sqrt{\frac{10\,{\rm MHz}}{2}} | ||
= 2.93\,{\rm Np} = 2.93\,{\rm Np} \cdot8.686\,\frac {\rm dB}{\rm Np} \hspace{0.15cm}\underline{ =25.5\,{\rm dB}}\hspace{0.05cm}.$$ | = 2.93\,{\rm Np} = 2.93\,{\rm Np} \cdot8.686\,\frac {\rm dB}{\rm Np} \hspace{0.15cm}\underline{ =25.5\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| Zeile 111: | Zeile 111: | ||
'''(4)''' Richig sind die <u>Aussagen 1 und 2</u>: | '''(4)''' Richig sind die <u>Aussagen 1 und 2</u>: | ||
| − | *Die Fouriertransformierte $H_1(f) = {\rm e}^{-A \hspace{0.05cm} \cdot \hspace{0.05cm} |f|}$ mit $A = 2 \hspace{0.05cm}\cdot \hspace{0.05cm} {a}_1/R$ ist reell und gerade, so dass $h_1(t)$ ebenfalls reell und gerade ist. | + | *Die Fouriertransformierte $H_1(f) = {\rm e}^{-A \hspace{0.05cm} \cdot \hspace{0.05cm} |f|}$ mit $A = 2 \hspace{0.05cm}\cdot \hspace{0.05cm} {a}_1/R$ ist reell und gerade, so dass $h_1(t)$ ebenfalls reell und gerade ist. |
*Aufgrund der Tiefpass–Charakteristik von $H_1(f)$ liegt das Maximum bei $t = 0$. | *Aufgrund der Tiefpass–Charakteristik von $H_1(f)$ liegt das Maximum bei $t = 0$. | ||
| − | *Die letzte Aussage ist dagegen falsch: Das Integral über $h_1(t)$ im gesamten Zeitbereich $ \pm \infty$ | + | *Die letzte Aussage ist dagegen falsch: Das Integral über $h_1(t)$ ist im gesamten Zeitbereich $ \pm \infty$ gleich $H_1(f=0) = 1$. |
| Zeile 119: | Zeile 119: | ||
'''(5)''' Richtig ist nur <u>der Lösungsvorschlag 1</u>: | '''(5)''' Richtig ist nur <u>der Lösungsvorschlag 1</u>: | ||
| − | *Die Teilimpulsantwort $h_1(t ) \star h_2(t )$ berücksichtigt den Einfluss von $\alpha_1$, $\alpha_2$ und $\beta_2$ und damit alle Terme, die zu Verzerrungen führen. | + | *Die Teilimpulsantwort $h_1(t ) \star h_2(t )$ berücksichtigt den Einfluss von $\alpha_1$, $\alpha_2$ und $\beta_2$ und damit alle Terme, die zu Verzerrungen führen. |
*Dagegen führt $\alpha_0$ nur zu einer frequenzunabhängigen Dämpfung und $\beta_1$ lediglich zu einer für alle Frequenzen konstanten Laufzeit. | *Dagegen führt $\alpha_0$ nur zu einer frequenzunabhängigen Dämpfung und $\beta_1$ lediglich zu einer für alle Frequenzen konstanten Laufzeit. | ||
| − | *Der Lösungsvorschlag 2 trifft dagegen nicht zu: Zunächst (bei kleinen $t$–Werten) ist $h_1(t ) \star h_2(t )$ kleiner als $h_2(t )$. Bei großen $t$–Werten liegt dann die blaue Kurve oberhalb der roten. | + | *Der Lösungsvorschlag 2 trifft dagegen nicht zu: Zunächst (bei kleinen $t$–Werten) ist $h_1(t ) \star h_2(t )$ kleiner als $h_2(t )$. |
| + | *Bei großen $t$–Werten liegt dann die blaue Kurve oberhalb der roten. | ||
*Das bedeutet: $\alpha_1$ und damit auch $h_1(t )$ bewirken tatsächlich zusätzliche Verzerrungen, auch wenn diese nicht sehr ins Gewicht fallen. | *Das bedeutet: $\alpha_1$ und damit auch $h_1(t )$ bewirken tatsächlich zusätzliche Verzerrungen, auch wenn diese nicht sehr ins Gewicht fallen. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 24. November 2021, 13:51 Uhr
Das Zeitverhalten einer Kupferdoppelader mit Durchmesser $d = 0.5 \ \rm mm$ soll analysiert werden.
- Der Frequenzgang lautet mit der Leitungslänge $l = 1.5 \ \rm km$ und der Bitrate $R = 10 \rm Mbit/s$:
- $$H_{\rm K}(f) = {\rm e}^{-{\rm a}_0 } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 2 \pi \cdot f \hspace{0.05cm} \cdot \hspace{0.01cm}\tau_{\rm P}} \cdot {\rm e}^{-{\rm a}_1 \hspace{0.05cm}\cdot \hspace{0.02cm}2f/R}\cdot {\rm e}^{-{\rm a}_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}} \hspace{0.05cm}.$$
- Verwendet sind folgende Größen, die sich aus dem Dämpfungs– und Phasenmaß ableiten lassen:
- $${\rm a}_0 = \alpha_0 \cdot l\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm}\alpha_0 = 0.5066\,\, \frac{\rm Np}{\rm km}\hspace{0.05cm},$$
- $$ \tau_{\rm P} = \frac{\beta_1 \cdot l}{2 \pi} \hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm}\beta_1 = 30.6\,\, \frac{\rm rad}{\rm km \cdot MHz}\hspace{0.05cm},$$
- $$ {\rm a}_1 = \alpha_1 \cdot l \cdot {{R}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm} \alpha_1 = 0.136\,\, \frac{\rm Np}{\rm km \cdot MHz}\hspace{0.05cm},$$
- $$ {\rm a}_2 = \alpha_2 \cdot l \cdot \sqrt{{R}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm} \alpha_2 = 1.1467\,\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}}\hspace{0.05cm},$$
- $$ {b}_2 = \beta_2 \cdot l \cdot \sqrt{{R}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm} \beta_2 = 1.1467\,\, \frac{\rm rad}{\rm km \cdot \sqrt{MHz}}\hspace{0.05cm}.$$
- Die Impulsantwort lässt sich somit in der Form
- $$h_{\rm K}(t ) = K \cdot \big [ \delta(t - \tau_{\rm P})\star h_{1}(t) \star h_{2}(t) \big ]$$
- darstellen, wobei
- die Teilimpulsantwort $h_1(t)$ auf den dritten Term in obiger Gleichung $H_{\rm K}(f)$ zurückgeht, und
- $h_2(t)$ die gemeinsame Zeitbereichsdarstellung der beiden letzten Terme angibt.
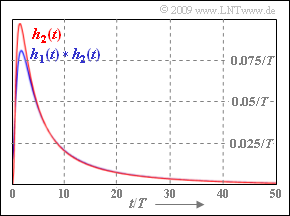
Die Grafik zeigt als rote Kurve den Anteil $h_2(t)$ der Impulsantwort und das Faltungsprodukt $h_1(t) \star h_2(t)$ ⇒ blauer Kurvenverlauf.
Dabei ist $h_2(t)$ gleich der Koaxialkabel–Impulsantwort mit der charakteristischen Kabeldämpfung ${\rm a}_\star = {\rm a}_2$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Eigenschaften von Kupfer–Doppeladern.
- Die Parameter $\alpha_0$, $\alpha_1$ und $\alpha_2$ wurden aus den $k$–Parametern umgerechnet, wie in Aufgabe 4.6 gezeigt.
- Der Phasenmaßparameter $\beta_2$ wurde hier zahlenmäßig gleich dem Dämpfungsmaßparameter $\alpha_2$ gesetzt.
- Der Dämpfungsanteil ${\rm a}_2$ und der Phasenanteil ${b}_2$ unterscheiden sich deshalb nur in der Einheit.
- Auf der Seite Diskussion der gefundenen Näherungslösung wird dargelegt, warum diese Maßnahme erforderlich ist.
- Sie können zur Überprüfung Ihrer Ergebnisse das interaktive Applet Zeitverhalten von Kupferkabeln benutzen.
Fragebogen
Musterlösung
- $$K = {\rm e}^{-{\rm a}_0 }= {\rm e}^{-0.76} \hspace{0.15cm}\underline{= 0.468} \hspace{0.05cm}.$$
(2) Für die Phasenlaufzeit gilt mit der angegebenen Gleichung:
- $$\tau_{\rm P} = \frac{\beta_1 \cdot l}{2 \pi}= \frac{30.6 \cdot 1.5}{2 \pi}\, {\rm µ s}\approx 7.31\, {\rm µ s}\hspace{0.05cm},$$
und auf die Symboldauer $T = 0.1 \ µ \rm s$ bezogen:
- $${\tau_{\rm P}}/{T} \hspace{0.15cm}\underline{ \approx 73}\hspace{0.05cm}.$$
(3) Die Impulsantwort eines Koaxialkabels ist näherungsweise gleich $h_2(t)$, wenn das Kabel folgende charakteristische Kabeldämpfung aufweist:
- $${\rm a}_\star ={\rm a}_2 = \alpha_2 \cdot l \cdot \sqrt{{R}/{2}} = 1.1467\,\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}} \cdot 1.5\,{\rm km} \cdot \sqrt{\frac{10\,{\rm MHz}}{2}} = 2.93\,{\rm Np} = 2.93\,{\rm Np} \cdot8.686\,\frac {\rm dB}{\rm Np} \hspace{0.15cm}\underline{ =25.5\,{\rm dB}}\hspace{0.05cm}.$$
(4) Richig sind die Aussagen 1 und 2:
- Die Fouriertransformierte $H_1(f) = {\rm e}^{-A \hspace{0.05cm} \cdot \hspace{0.05cm} |f|}$ mit $A = 2 \hspace{0.05cm}\cdot \hspace{0.05cm} {a}_1/R$ ist reell und gerade, so dass $h_1(t)$ ebenfalls reell und gerade ist.
- Aufgrund der Tiefpass–Charakteristik von $H_1(f)$ liegt das Maximum bei $t = 0$.
- Die letzte Aussage ist dagegen falsch: Das Integral über $h_1(t)$ ist im gesamten Zeitbereich $ \pm \infty$ gleich $H_1(f=0) = 1$.
(5) Richtig ist nur der Lösungsvorschlag 1:
- Die Teilimpulsantwort $h_1(t ) \star h_2(t )$ berücksichtigt den Einfluss von $\alpha_1$, $\alpha_2$ und $\beta_2$ und damit alle Terme, die zu Verzerrungen führen.
- Dagegen führt $\alpha_0$ nur zu einer frequenzunabhängigen Dämpfung und $\beta_1$ lediglich zu einer für alle Frequenzen konstanten Laufzeit.
- Der Lösungsvorschlag 2 trifft dagegen nicht zu: Zunächst (bei kleinen $t$–Werten) ist $h_1(t ) \star h_2(t )$ kleiner als $h_2(t )$.
- Bei großen $t$–Werten liegt dann die blaue Kurve oberhalb der roten.
- Das bedeutet: $\alpha_1$ und damit auch $h_1(t )$ bewirken tatsächlich zusätzliche Verzerrungen, auch wenn diese nicht sehr ins Gewicht fallen.