Digitalsignalübertragung/Viterbi–Empfänger: Unterschied zwischen den Versionen
| Zeile 47: | Zeile 47: | ||
== Fehlergrößen und Gesamtfehlergrößen== | == Fehlergrößen und Gesamtfehlergrößen== | ||
<br> | <br> | ||
| − | Wie im Kapitel [[Digitalsignalübertragung/Optimale_Empfängerstrategien|Optimale Empfängerstrategien]] gibt $Q \in \{Q_i\}$ die begrenzte, aus $N$ Binärsymbolen bestehende Quellensymbolfolge an. | + | Wie im Kapitel [[Digitalsignalübertragung/Optimale_Empfängerstrategien|Optimale Empfängerstrategien]] gibt $Q \in \{Q_i\}$ die begrenzte, aus $N$ Binärsymbolen bestehende Quellensymbolfolge an. |
| − | *Die Anzahl der möglichen Symbolfolgen $Q_i$ ist somit $2^N$. | + | *Die Anzahl der möglichen Symbolfolgen $Q_i$ ist somit $2^N$. |
| − | *$V$ bezeichnet die Sinkensymbolfolge der Länge $N$, die vom Viterbi–Entscheider gleich der wahrscheinlichsten Folge $Q_j$ gesetzt wird.<br> | + | |
| + | *$V$ bezeichnet die Sinkensymbolfolge der Länge $N$, die vom Viterbi–Entscheider gleich der wahrscheinlichsten Folge $Q_j$ gesetzt wird.<br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Definitionen:}$ |
| + | *Die '''Fehlergröße''' $\varepsilon_{\nu}(i)$ bezeichnet die quadratische Abweichung zwischen dem tatsächlichen, verrauschten Abtastwert $d_\nu$ und dem zur Folge $Q_i$ gehörenden Nutzabtastwert $d_{ {\rm S}\nu}$: | ||
:$$\varepsilon_{\nu}(i) = \vert d_{\nu} - d_{ {\rm S}\nu}(i) \vert^2 | :$$\varepsilon_{\nu}(i) = \vert d_{\nu} - d_{ {\rm S}\nu}(i) \vert^2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In der Literatur findet man hierfür auch die Bezeichnung & | + | :In der Literatur findet man hierfür auch die Bezeichnung "Teilmetrik" (englisch: "metric"). |
| − | + | * Die '''Gesamtfehlergröße''' $\gamma_{\nu}(i)$ kennzeichnet die Summe aller Fehlergrößen bis zum Zeitpunkt $\nu$:<br> | |
| − | |||
| − | |||
:$$\gamma_{\nu}(i)= \sum_{k=0}^{\nu}\varepsilon_{k}(i) | :$$\gamma_{\nu}(i)= \sum_{k=0}^{\nu}\varepsilon_{k}(i) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Man spricht in diesem Zusammenhang auch von | + | :Man spricht in diesem Zusammenhang auch von "akkumulierten Metrik" (englisch: "accumulated metric").}} |
| − | [[Datei:P ID1469 Dig T 3 8 S2b version1.png|right|frame| | + | [[Datei:P ID1469 Dig T 3 8 S2b version1.png|right|frame|Fehlergrößen $\varepsilon_{\nu}(i)$ und Gesamtfehlergrößen $\gamma_{\nu}(i)= \gamma_{\nu-1}(i\hspace{0.05cm}')+\varepsilon_{\nu}(i\hspace{0.05cm}'') |
| − | Die Grafik verdeutlicht die oben definierten Größen in einer Baumstruktur, woraus zu erkennen ist, dass die Gesamtfehlergrößen iterativ berechnet werden können: | + | \hspace{0.05cm}$ im Baumdiagramm. <u>Hinweise:</u> $\bullet$ $i$, $i\hspace{0.05cm}'$, $i\hspace{0.05cm}''$ sind unterschiedliche Laufvariable.<br> $\bullet$ Definition gilt für Grundimpuls mit Hauptwert $g_{0}$ und einem Vorläufer $g_{-1}$.<br> $\bullet$ Bei $v$ Vorläufern müsste die obige Summe bei $k = 1 -v$ beginnen.<br> $\bullet$ Der Parameter $i \in \{0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, 2^{N+1}-1\}$ wird meist binär dargestellt. <br> $\bullet$ Er beschreibt die Amplitudenkoeffizienten $a_1$, ... , $a_{\nu +1}$ $($jeweils $0$ oder $1)$.|class=fit]] |
| + | Die Grafik verdeutlicht die oben definierten Größen in einer Baumstruktur, woraus zu erkennen ist, dass die Gesamtfehlergrößen iterativ berechnet werden können: | ||
:$$\gamma_{\nu}(i)= \gamma_{\nu-1}(i\hspace{0.05cm}')+\varepsilon_{\nu}(i\hspace{0.05cm}'') | :$$\gamma_{\nu}(i)= \gamma_{\nu-1}(i\hspace{0.05cm}')+\varepsilon_{\nu}(i\hspace{0.05cm}'') | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Zu dieser Grafik ist weiter anzumerken: | |
| − | + | *Die Knoten des Baumdiagramms stehen für die "Gesamtfehlergrößen" $\gamma_{\nu}(i)$. Deren Anzahl wird mit jedem Iterationsschritt verdoppelt. Zum Zeitpunkt $\nu$ gibt es $2^{\nu+1}$ solcher Knoten, und für $\nu = 3$ genau $2^4 = 16$ Knoten zu erkennen.<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | *Die Knoten des Baumdiagramms stehen für die | ||
*Die zu den Gesamtfehlergrößen $\gamma_{\nu}(i)$ gehörigen <i>Amplitudenkoeffizienten</i> ergeben sich, wenn man den Weg vom Anfangsknoten bis zum betrachteten Knoten verfolgt. Es wird vereinbart, dass einem nach oben gerichteten Zweig der Koeffizient $a_\nu=1$ und einem nach unten gerichteten Zweig der Koeffizient $a_\nu=0$ zugeordnet wird.<br> | *Die zu den Gesamtfehlergrößen $\gamma_{\nu}(i)$ gehörigen <i>Amplitudenkoeffizienten</i> ergeben sich, wenn man den Weg vom Anfangsknoten bis zum betrachteten Knoten verfolgt. Es wird vereinbart, dass einem nach oben gerichteten Zweig der Koeffizient $a_\nu=1$ und einem nach unten gerichteten Zweig der Koeffizient $a_\nu=0$ zugeordnet wird.<br> | ||
Version vom 3. Juli 2022, 16:31 Uhr
Inhaltsverzeichnis
- 1 Betrachtetes Szenario und Voraussetzungen
- 2 Fehlergrößen und Gesamtfehlergrößen
- 3 Minimale Gesamtfehlergrößen
- 4 Darstellung der minimalen Gesamtfehlergrößen – Trellisdiagramm
- 5 Vereinfachtes Trellisdiagramm
- 6 Erweiterung auf zwei Vorläufer
- 7 Fehlerwahrscheinlichkeit bei Maximum–Likelihood–Entscheidung
- 8 Aufgaben zum Kapitel
Betrachtetes Szenario und Voraussetzungen
Der "Korrelationsempfänger" ist im Sinne der Maximum–Likelihood–Entscheidungsregel optimal, das heißt, er führt bei gleichwahrscheinlichen Quellensymbolen zur minimalen Fehlerwahrscheinlichkeit. Nachteilig ist:
- Der Realisierungsaufwand steigt exponentiell mit der Länge $N$ der zu detektierenden Symbolfolge.
- Da die Folge gemeinsam entschieden wird, kommt es bei großem $N$ zu langen Verzögerungen.
In den 1970er Jahren hat Andrew J. Viterbi einen Maximum–Likelihood–Empfänger vorgeschlagen, der die Detektion von Teilen der empfangenen Nachricht erlaubt und bei dem sich der Realisierungsaufwand auch bei unendlich langen Folgen in Grenzen hält.
Zu den einzelnen Komponenten des Blockschaltbildes ist anzumerken:
- Das an den Empfangsgrundimpuls $g_r(t)$ und die Störung angepasste "Matched–Filter" $H_{\rm MF}(f)$ dient der "Störleistungsbegrenzung". Das MF–Ausgangssignal $m(t)$ bzw. die Folge $\langle m_\nu \rangle$ der äquidistanten Signalwerte nach der Abtastung besitzt das bestmögliche Signal–zu–Stör–Leistungsverhältnis $\rm (SNR)$.
- Aufgabe des Dekorrelationsfilters $H_{\rm DF}(f)$ ist es, aus der Folge $\langle m_\nu \rangle$ die Detektionsabtastwerte $d_\nu = d_{{\rm S}\nu} + d_{{\rm N}\nu}$ zu gewinnen, deren Störanteile $d_{{\rm N}\nu}$ unkorreliert sind. Dieses Filter wird deshalb auch "Whitening–Filter" genannt.
- Der Viterbi–Entscheider, der im Mittelpunkt der folgenden Betrachtungen steht, gewinnt aus der Folge $\langle d_\nu \rangle $ seiner wertkontinuierlichen Eingangswerte die binäre Ausgangsfolge $\langle v_\nu \rangle$ entsprechend der Maximum–Likelihood–Regel mit der kleinstmöglichen Fehlerwahrscheinlichkeit ${\rm Pr}(v_\nu \ne q_\nu)$.
Um den Viterbi–Algorithmus möglichst einfach beschreiben zu können, werden hier einige vereinfachende Voraussetzungen getroffen:
- Die Amplitudenkoeffizienten seien unipolar ⇒ $a_\nu \in \{0,\hspace{0.05cm} 1\}$. Anzumerken ist, dass es bei der Verwendung bipolarer Koeffizienten ⇒ $a_\nu \in \{-1,\hspace{0.05cm} +1\}$ nur einiger weniger Modifikationen bedarf. Diese Schwierigkeiten betreffen eher die Beschreibung als die Implementierung.
- Der Grundimpuls $g_d(t)$ nach dem Dekorrelationsfilters $H_{\rm DF}(f)$ besteht nur aus dem Hauptwert $g_0 = g_d(t = T_{\rm D})$ und dem Vorläufer $g_{-1} = g_d(t = T_{\rm D}-T)$. Nachläufer gibt es in unserem Modell nicht: $g_{\nu} = g_d(t = T_{\rm D}+\nu \cdot T)=0$. Auch weitere Vorläufer seien vorerst ausgeschlossen: $g_{-2} = g_{-3}= \text{ ...} = 0$.
- Für den Abtastwert des wertkontinuierlichen $\rm DF$–Ausgangssignals $d(t)$ zum Zeitpunkt $\nu \cdot T$ erhält man das Ergebnis: $d_{\nu} = a_{\nu}\cdot g_{0} + a_{\nu+1}\cdot g_{-1}+d_{{\rm N}\nu}\hspace{0.05cm}$, wobei die Rauschkomponente $d_{{\rm N}\nu}$ als gaußverteilt mit Standardabweichung $\sigma_d$ angenommen wird.
Hinweise:
Bei bipolarer Signalisierung ist der Algorithmus nicht aufwändiger. $\bullet$ Dagegen steigt der Rechenaufwand, wenn der Grundimpuls $g_d(t)$ breiter wird und mehr als nur einen Vorläufer $g_{-1}$ aufweist. $\bullet$ Die Vernachlässigung von Nachläufern in der Beschreibung ist keine grundlegende Einschränkung, weil jeder Impuls diese Bedingung durch geeignete Wahl des Detektionszeitpunktes $T_{\rm D}$ erfüllen kann. $\bullet$ Im Folgenden werden alle Signalwerte auf $1$ normiert.
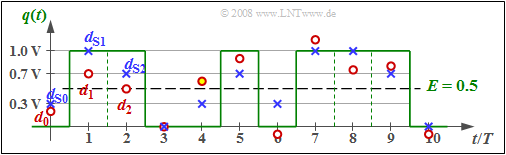
$\text{Beispiel 1:}$ In der Grafik sind als (blaue) Kreuze die Detektionsnutzabtastwerte $d_{ {\rm S}\nu}$ eingetragen, wobei die zugehörigen Amplitudenkoeffizienten $a_1 = 1$, $a_2 = 1$, $a_3 = 0$, ... aus dem grün eingezeichneten Quellensignal $q(t)$ abgelesen werden können.
Die Grundimpulswerte sind in diesem Beispiel zu $g_0 = 0.7$ und $g_{-1} = 0.3$ angenommen. Es ist weiter zu erkennen, dass $d_{ {\rm S}\nu}$ nur vier verschiedene Werte annehmen kann, nämlich $0$, $g_{-1}=0.3$, $g_0= 0.7$ und $g_0 +g_{-1}= 1$.
Die am Viterbi–Entscheider anstehenden Abtastwerte (rote Punkte) sind $d_0 = 0.2$, $d_1 = 0.7$, $d_2 = 0.5$, $d_3 = 0$, ... , wobei die Differenzen $d_{ {\rm N}\nu} = d_\nu - d_{ {\rm S}\nu}$ von einer AWGN–Rauschquelle herrühren.
- Ein Schwellenwertentscheider $($mit der Schwelle bei $E = 0.5)$ würde bei diesen dargestellten zehn Bit mindestens eine Fehlentscheidung treffen $($zur Zeit $t = 4T)$, und eventuell eine weitere bei $t = 2T$, falls der Abtastwert $d_2 = 0.5$ doch geringfügig kleiner ist als der Schwellenwert $E = 0.5$.
- Dagegen wird der Viterbi–Empfänger diese Folge der Länge $10$ richtig entscheiden, wie auf den nächsten Seiten gezeigt wird.
Fehlergrößen und Gesamtfehlergrößen
Wie im Kapitel Optimale Empfängerstrategien gibt $Q \in \{Q_i\}$ die begrenzte, aus $N$ Binärsymbolen bestehende Quellensymbolfolge an.
- Die Anzahl der möglichen Symbolfolgen $Q_i$ ist somit $2^N$.
- $V$ bezeichnet die Sinkensymbolfolge der Länge $N$, die vom Viterbi–Entscheider gleich der wahrscheinlichsten Folge $Q_j$ gesetzt wird.
$\text{Definitionen:}$
- Die Fehlergröße $\varepsilon_{\nu}(i)$ bezeichnet die quadratische Abweichung zwischen dem tatsächlichen, verrauschten Abtastwert $d_\nu$ und dem zur Folge $Q_i$ gehörenden Nutzabtastwert $d_{ {\rm S}\nu}$:
- $$\varepsilon_{\nu}(i) = \vert d_{\nu} - d_{ {\rm S}\nu}(i) \vert^2 \hspace{0.05cm}.$$
- In der Literatur findet man hierfür auch die Bezeichnung "Teilmetrik" (englisch: "metric").
- Die Gesamtfehlergröße $\gamma_{\nu}(i)$ kennzeichnet die Summe aller Fehlergrößen bis zum Zeitpunkt $\nu$:
- $$\gamma_{\nu}(i)= \sum_{k=0}^{\nu}\varepsilon_{k}(i) \hspace{0.05cm}.$$
- Man spricht in diesem Zusammenhang auch von "akkumulierten Metrik" (englisch: "accumulated metric").
$\bullet$ Definition gilt für Grundimpuls mit Hauptwert $g_{0}$ und einem Vorläufer $g_{-1}$.
$\bullet$ Bei $v$ Vorläufern müsste die obige Summe bei $k = 1 -v$ beginnen.
$\bullet$ Der Parameter $i \in \{0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, 2^{N+1}-1\}$ wird meist binär dargestellt.
$\bullet$ Er beschreibt die Amplitudenkoeffizienten $a_1$, ... , $a_{\nu +1}$ $($jeweils $0$ oder $1)$.
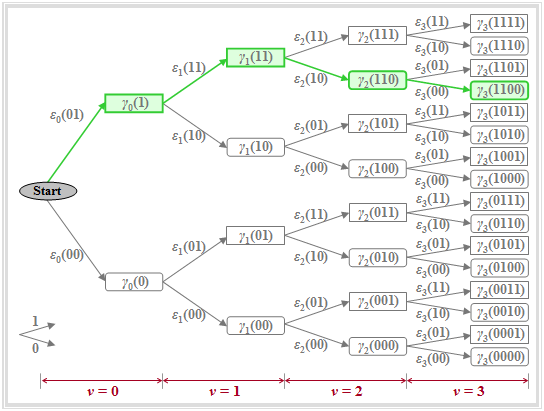
Die Grafik verdeutlicht die oben definierten Größen in einer Baumstruktur, woraus zu erkennen ist, dass die Gesamtfehlergrößen iterativ berechnet werden können:
- $$\gamma_{\nu}(i)= \gamma_{\nu-1}(i\hspace{0.05cm}')+\varepsilon_{\nu}(i\hspace{0.05cm}'') \hspace{0.05cm}.$$
Zu dieser Grafik ist weiter anzumerken:
- Die Knoten des Baumdiagramms stehen für die "Gesamtfehlergrößen" $\gamma_{\nu}(i)$. Deren Anzahl wird mit jedem Iterationsschritt verdoppelt. Zum Zeitpunkt $\nu$ gibt es $2^{\nu+1}$ solcher Knoten, und für $\nu = 3$ genau $2^4 = 16$ Knoten zu erkennen.
- Die zu den Gesamtfehlergrößen $\gamma_{\nu}(i)$ gehörigen Amplitudenkoeffizienten ergeben sich, wenn man den Weg vom Anfangsknoten bis zum betrachteten Knoten verfolgt. Es wird vereinbart, dass einem nach oben gerichteten Zweig der Koeffizient $a_\nu=1$ und einem nach unten gerichteten Zweig der Koeffizient $a_\nu=0$ zugeordnet wird.
- Beispielsweise kennzeichnet der grün hinterlegte Knoten $\gamma_{3}(\rm 1100)$ die Gesamtfehlergröße unter der hypothetischen Annahme, dass die Symbole $a_1=1$, $a_2=1$, $a_3=0$, $a_4=0$ gesendet wurden. Diese Zuordnung kann auch aus den Richtungen der Pfeile im Baumdiagramm abgelesen werden: Zunächst zweimal nach oben, dann zweimal nach unten.
- Aufgrund des Vorläufers muss bereits zum Zeitpunkt $\nu = 3$ der Koeffizient $a_4$ mitberücksichtigt werden. Alle Knoten $\gamma_{\nu}(i)$, die unter der Voraussetzung $a_{\nu +1}=1$ berechnet werden, sind im Baumdiagramm durch Rechtecke dargestellt, während die Hypothese $a_{\nu +1}=0$ jeweils durch ein abgerundetes Rechteck symbolisiert ist, zum Beispiel $\gamma_{2}(\rm 110)$ oder $\gamma_{3}(\rm 1100)$.
- Die Zweige im Baumdiagramm sind den Fehlergrößen $\varepsilon_{\nu}(i)$ zugeordnet. Beim vorausgesetzten Grundimpuls (nur $g_{0}$ und $g_{-1}$ sind ungleich Null) gibt es zu jedem Zeitpunkt mit Ausnahme des Startzustandes $(\nu = 0)$ genau vier unterschiedliche Größen:
- $$\varepsilon_{\nu}(00) = |d_{\nu}|^2\hspace{0.05cm},\hspace{0.5cm}\varepsilon_{\nu}(01) = |d_{\nu}-g_{-1}|^2\hspace{0.05cm},\hspace{0.2cm} \varepsilon_{\nu}(10) = |d_{\nu}-g_{0}|^2\hspace{0.05cm},\hspace{0.2cm}\varepsilon_{\nu}(11) = |d_{\nu}-g_{0}-g_{-1}|^2\hspace{0.05cm}.$$
- Die Gesamtfehlergröße $\gamma_{\nu}(i)$ ist gleich der Summe aus dem vorausgegangenen Knoten $\gamma_{\nu-1}(i\hspace{0.05cm}')$ und dem dazwischenliegenden Zweig $\varepsilon_{\nu}(i\hspace{0.05cm}'')$. Beispielsweise gilt für die hervorgehobenen Knoten:
- $$\gamma_{1}(11)=\gamma_{0}(1)+\varepsilon_{1}(11) ,\hspace{0.25cm} \gamma_{2}(110)=\gamma_{1}(11)+\varepsilon_{2}(10) ,\hspace{0.25cm} \gamma_{3}(1100)=\gamma_{2}(110)+\varepsilon_{3}(00).$$
- Bei den ersten Knoten $\gamma_{0}(0)$ und $\gamma_{0}(1)$ wird berücksichtigt, dass vor der eigentlichen Übertragung $(a_1$, $a_2$, ...$)$ vereinbarungsgemäß stets das Symbol $a_0 = 0$ übertragen wird. Daraus folgt:
- $$\gamma_{0}(0)=\varepsilon_{0}(00)= |d_{0}|^2 \hspace{0.05cm},\hspace{0.2cm} \gamma_{0}(1)=\varepsilon_{0}(01)=|d_{0}-g_{-1}|^2 \hspace{0.05cm}.$$
Die beiden folgenden Beispiele werden hoffentlich diese etwas ermüdenden Aussagen verdeutlichen.
$\text{Beispiel 2:}$ Wir betrachten wie im $\text{Beispiel 1}$ die unipolare Quellensymbolfolge der Länge $N=3$ mit folgenden Parameterwerten:
- $$g_{0}=0.7 \hspace{0.05cm},\hspace{0.2cm} g_{-1}=0.3 \hspace{0.05cm},\hspace{0.2cm} d_{0}=0.2 \hspace{0.05cm},\hspace{0.2cm} d_{1}=0.7 \hspace{0.05cm},\hspace{0.2cm} d_{2}=0.5 \hspace{0.05cm},\hspace{0.2cm} d_{3}=0 \hspace{0.05cm} \hspace{0.05cm}.$$
Dann gilt für die Fehlergrößen $\varepsilon_{\nu}(i)$ zu den Zeitpunkten $\nu = 0$ bis $\nu = 3$:
- $$\nu = 0\text{:} \hspace{0.2cm}\varepsilon_{0}(00) = \big [0.2- (0 \cdot 0.7 + 0 \cdot 0.3) \big ]^2=0.04 \hspace{0.05cm},\hspace{0.4cm} \varepsilon_{0}(01) = \big [0.2- (0 \cdot 0.7 + 1 \cdot 0.3) \big ]^2=0.01 \hspace{0.05cm};$$
- $$\nu = 1{:} \hspace{0.2cm}\varepsilon_{1}(00) = \big [0.7- (0 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.49 \hspace{0.05cm},\hspace{0.4cm} \varepsilon_{1}(01) = \big [0.7- (0 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.16 \hspace{0.05cm},$$
- $$\hspace{1.4cm}\varepsilon_{1}(10) = \big [0.7- (1 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.00 \hspace{0.05cm}\hspace{0.4cm}\varepsilon_{1}(11) = \big [0.7- (1 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.09 \hspace{0.05cm};$$
- $$\nu = 2\text{:} \hspace{0.2cm}\varepsilon_{2}(00) = \big [0.5- (0 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.25 \hspace{0.05cm},\hspace{0.4cm}\varepsilon_{2}(01) = \big [0.5- (0 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.04 \hspace{0.05cm},$$
- $$\hspace{1.4cm}\varepsilon_{2}(10) = \big [0.5- (1 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.04 \hspace{0.05cm},\hspace{0.4cm}\varepsilon_{2}(11) = \big [0.5- (1 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.25 \hspace{0.05cm};$$
- $$ \nu = 3\text{:} \hspace{0.2cm}\varepsilon_{3}(00) = \big [0.0- (0 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.00 \hspace{0.05cm},\hspace{0.4cm}\varepsilon_{3}(01) = \big [0.0- (0 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=0.09 \hspace{0.05cm},$$
- $$\hspace{1.4cm}\varepsilon_{3}(10) = \big [0.0- (1 \cdot 0.7 + 0 \cdot 0.3)\big ]^2=0.49 \hspace{0.05cm},\hspace{0.4cm}\varepsilon_{3}(11) = \big [0.0- (1 \cdot 0.7 + 1 \cdot 0.3)\big ]^2=1.00 \hspace{0.05cm}.$$
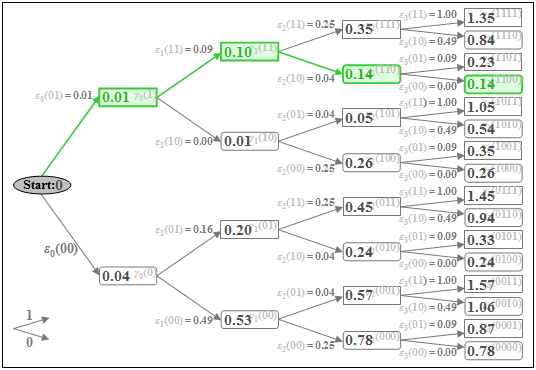
$\text{Beispiel 3:}$ Mit den im $\text{Beispiel 2}$ ermittelten Fehlergrößen $\varepsilon_{\nu}(i)$ können nun auch die Gesamtfehlergrößen $\gamma_{\nu}(i)$ berechnet werden. Nachfolgend ist das Baumdiagramm mit den Gesamtfehlergrößen $\gamma_{\nu}(i)$ als Knoten für die Zeitpunkte $\nu = 0$ bis $\nu = 3$ dargestellt.
Die minimale Gesamtfehlergröße zum Zeitpunkt $\nu = 3$ ist $\gamma_{3}(\rm 1100) = 0.14$. Daraus ergeben sich die Koeffizienten der nach den vorliegenden Signalwerten $d_0 = 0.2$, $d_1 = 0.7$, $d_2 = 0.5$ und $d_3 = 0$ mit größter Wahrscheinlichkeit gesendeten (unipolaren) Folge zu $a_1 = 1$, $a_2 = 1$ und $a_3 = 0$ (grüner Pfad).
Weiter ist anzumerken:
- Ist die Folgenlänge $N = 3$ (das heißt: nur drei Symbole werden durch den Viterbi–Empfänger gemeinsam entschieden), so ist auch die Entscheidung $a_4 = 0$ mit Sicherheit die richtige, da alle Koeffizienten $a_{\nu>3}$ als Null vorausgesetzt wurden.
- Bei längerer Folge $(N > 3)$ kann aber aus dem minimalen Wert $\gamma_{3}(\rm 1100)$ nicht unbedingt geschlossen werden, dass $a_1 = 1$, $a_2 = 1$, $a_3 = 0$ tatsächlich Teil der wahrscheinlichsten Folge ist. Bei Berücksichtigung weiterer Abtastwerte $(d_4$, $d_5$, ...$)$ könnte sich dieses vorläufige Ergebnis durchaus noch ändern.
Minimale Gesamtfehlergrößen
Wir gehen weiterhin von den Zahlenwerten der letzten Beispiele aus:
- $$d_{0}=0.2 ,\hspace{0.1cm} d_{1}=0.7 ,\hspace{0.1cm} d_{2}=0.5 ,\hspace{0.1cm} d_{3}=0 ,$$
- $$g_{0}=0.7 ,\hspace{0.1cm} g_{-1}=0.3 .$$
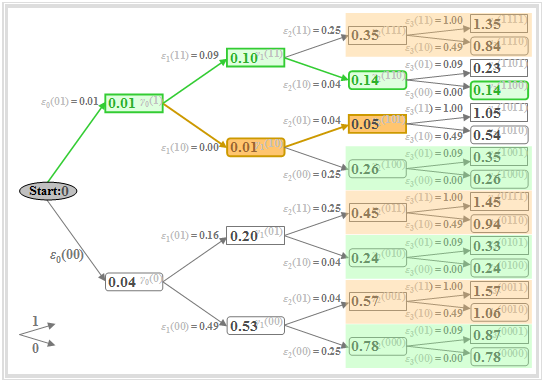
Damit ändert sich auch am Baumdiagramm gegenüber dem $\text{Beispiel 3}$ nichts. Durch einige farbliche Markierungen in dieser Grafik wird nur angedeutet, in welcher Weise das Baumdiagramm entsprechend den Vorschlägen von Viterbi vereinfacht werden kann.
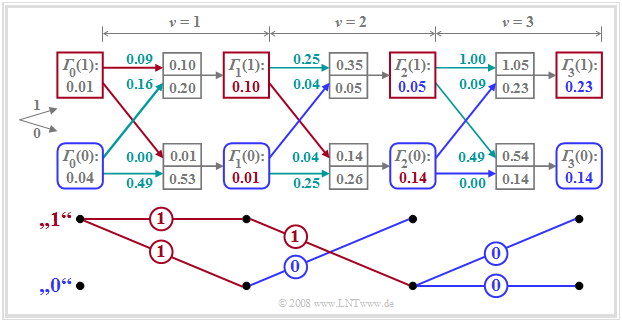
Wichtige Eigenschaften des Viterbi–Entscheiders lassen sich in obiger Grafik beispielsweise zum Zeitpunkt $\nu = 2$ erkennen:
- Zum Zeitpunkt $\nu = 2$ ist die minimale Gesamtfehlergröße $\gamma_{2}(\rm 101) = 0.05$ (braun hervorgehoben). Das bedeutet: Eine Entscheidung bei $\nu = 2$ – basierend auf $d_0$, $d_1$ und $d_2$ – wäre zugunsten der Folge $\rm 101$ anstelle der gesendeten Folge $\rm 110$ ausgegangen.
- Daraus folgt: Eine zu frühe endgültige Festlegung sollte unbedingt vermieden werden. Allerdings kann man zu jedem Zeitpunkt $\nu$ bereits mehrere Teilsymbolfolgen ausschließen, die zu späteren Zeitpunkten nicht mehr berücksichtigt werden müssen.
- Zu $\gamma_{2}(\rm 111) = 0.35$ werden die gleichen Fehlergrößen $\varepsilon_{3}(\rm 11)$ bzw. $\varepsilon_{3}(\rm 10)$ hinzuaddiert wie zu $\gamma_{2}(\rm 101) = 0.05$. Wegen $\gamma_{2}(\rm 111) > \gamma_{2}(\rm 101)$ steht somit bereits bei $\nu = 2$ fest, dass $\rm 111$ nicht Bestandteil der wahrscheinlichsten Folge sein kann. Gleiches gilt für $\rm 001$ und $\rm 011$. Diese Knoten und alle ihre Nachfahren müssen deshalb nicht weiter beachtet werden (braune Überdeckungen).
- Auch die abgerundeten Knoten $\gamma_{2}(\rm 000) = 0.78$, $\gamma_{2}(\rm 010) = 0.24$ und $\gamma_{2}(\rm 100) = 0.26$ sind nicht Bestandteil der wahrscheinlichsten Folge, da sie größer sind als der grün markierte Knoten $\gamma_{2}(\rm 110) = 0.14$. Auch diese und ihre Nachfahren müssen ab dem Zeitpunkt $\nu = 3$ nicht mehr berücksichtigt werden (grüne Überdeckungen).
$\text{Fazit:}$
- Von den acht Knoten bei $\nu = 2$ müssen nur zwei weiterverfolgt werden, nämlich das Rechteck $\gamma_{2}(\rm 101) = 0.05$ und das abgerundete Rechteck $\gamma_{2}(\rm 110) = 0.14$.
- Diese beschreiben die minimalen Gesamtfehlergrößen unter der Annahme, dass $a_3 = 0$ bzw. $a_3 = 1$ wäre.
Darstellung der minimalen Gesamtfehlergrößen – Trellisdiagramm
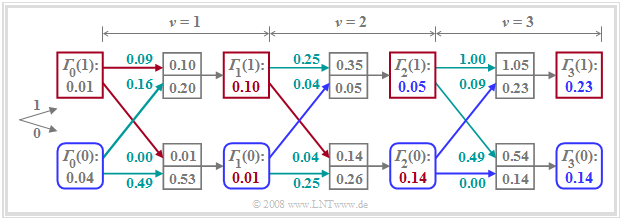
Wir verallgemeinern nun das Ergebnis dieses Beispiels. Unter der weiterhin gültigen Annahme, dass der Grundimpuls neben dem Hauptwert $(g_0)$ nur einen Vorläufer $(g_{-1})$ aufweist, ergeben sich die beiden minimalen Gesamtfehlergrößen zum Zeitpunkt $\nu$ formal zu
- $${\it \Gamma}_{\nu}(0) = {\rm Min}\left[{\it \Gamma}_{\nu-1}(0) + \varepsilon_{\nu}(00), \hspace{0.2cm}{\it \Gamma}_{\nu-1}(1) + \varepsilon_{\nu}(10)\right] \hspace{0.05cm},$$
- $${\it \Gamma}_{\nu}(1) = {\rm Min}\left[{\it \Gamma}_{\nu-1}(0) + \varepsilon_{\nu}(01), \hspace{0.2cm}{\it \Gamma}_{\nu-1}(1) + \varepsilon_{\nu}(11)\right] \hspace{0.05cm}.$$
Das Verfahren der Gesamtfehlerminimierung lässt sich im Trellisdiagramm anschaulich darstellen.
Ein Vergleich mit den Bildern auf den letzten Seiten zeigt:
- Der untere Zweig stellt die minimale Gesamtfehlergröße ${\it \Gamma}_{\nu}(0)$ dar, die zu jedem Zeitpunkt $\nu$ unter der Hypothese berechnet wird, dass $a_{\nu + 1} = 0$ gelten wird (blaue abgerundete Quadrate).
- Dagegen beschreibt der obere Zweig die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\nu}(1)$ unter der Annahme $a_{\nu + 1} = 1$ (rote Quadrate). Auch hier sind die Zahlenwerte an das bisherige Beispiel angepasst.
- Außer ${\it \Gamma}_{\nu}(0)$ und ${\it \Gamma}_{\nu}(1)$ muss der Maximum–Likelihood–Entscheider auch die dazugehörigen Symbolfolgen (Pfade) abspeichern. Diese Zweige sind in der Grafik rot bzw. blau hervorgehoben.
- Falls ${\it \Gamma}_{\nu}$ aus dem Knoten ${\it \Gamma}_{\nu-1}(0)$ hervorgeht – also wenn der untere der beiden ankommenden Zweige hervorgehoben ist – so ist das dazugehörige Symbol $\rm 0$, andernfalls das Symbol $\rm 1$.
- Zur Zeit $\nu = 3$ ergeben sich zum Beispiel sowohl ${\it \Gamma}_{3}(0) = 0.14$ als auch ${\it \Gamma}_{3}(1) = 0.23$ aus dem Vorgänger ${\it \Gamma}_{2}(0)$, so dass beide ausgewählte Pfade jeweils auf das Symbol $\rm 0$ verweisen (blaue Zweige).
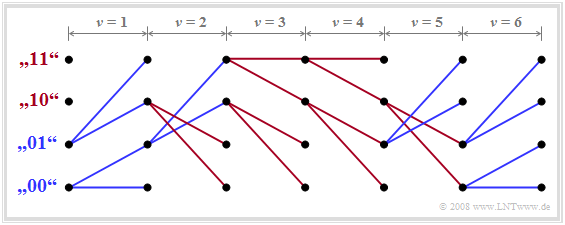
Vereinfachtes Trellisdiagramm
Der Vorteil des Trellisdiagramms besteht darin, dass sich die Anzahl der Knoten und Zweige nicht bei jedem Iterationsschritt verdoppeln. Durch die Auswahl der minimalen Gesamtfehlergrößen werden nur noch diejenigen Symbolfolgen weiter betrachtet, die als Teil der wahrscheinlichsten Folge überhaupt noch in Frage kommen.
Das Trellisdiagramm lässt sich weiter vereinfachen, indem man nur noch die ausgewählten Zweige einzeichnet. Dies ist im unteren Teil der Grafik an unserem Zahlenbeispiel verdeutlicht. Zur Erinnerung: Die tatsächlich gesendeten Amplitudenkoeffizienten seien $a_1= 1$, $a_2= 1$ und $a_3= 0$, und das oben gezeichnete Trellisdiagramm wurde unter der Annahme berechnet, dass aufgrund der Impulswerte $g_{-1} = 0.3$ und $g_{0} = 0.7$ sowie des AWGN–Rauschens die Eingangswerte $d_0= 0.2$, $d_1= 0.7$, $d_2= 0.5$ und $d_3= 0$ am ML–Entscheider anliegen.
Dieses vereinfachte Trellisdiagramm erlaubt folgende Aussagen:
- Die Entscheidung über $a_1= 1$ kann sofort zum Zeitpunkt $\nu = 1$ getroffen werden, da sich unter beiden Hypothesen – nämlich das nachfolgende Symbol sei $a_2= 0$ bzw. dieses Symbol sei $a_2= 1$ – das gleiche Resultat $a_1= 1$ ergibt.
- Dagegen kann zum Zeitpunkt $\nu = 2$ die endgültige Entscheidung über $a_2$ noch nicht getroffen werden. Unter der Annahme, dass $a_3= 0$ sein wird, müsste man sich für $a_2= 1$ entscheiden, während die Hypothese $a_3= 1$ zur Festlegung auf $a_2= 0$ führen würde.
- Zur Zeit $\nu = 3$ ist die Entscheidung für $a_1= 1$, $a_2= 1$, $a_3= 0$ endgültig, da beide durchgehenden Pfade diese (die in diesem Fall richtige) Folge suggerieren.
- Würde man die Entscheidung auf den Zeitpunkt $\nu = 4$ verschieben, so hätte man nicht mehr nutzbare Information über $a_1$, $a_2$ und $a_3$ zur Verfügung.
Alle Aussagen dieses Kapitels können mit dem interaktiven Applet Viterbi–Empfänger für einen Vorläufer verifiziert werden.
Erweiterung auf zwei Vorläufer
Wird der Grundimpuls durch die Abtastwerte $g_{0} \ne 0$, $g_{-1} \ne 0$ und $g_{-2} \ne 0$ beschrieben, so müssen im Trellisdiagramm zu jedem Zeitpunkt $\nu$ vier Metriken ${\it \Gamma}_{\nu}(00)$, ${\it \Gamma}_{\nu}(01)$, ${\it \Gamma}_{\nu}(10)$ und ${\it \Gamma}_{\nu}(11)$ bestimmt werden. ${\it \Gamma}_{\nu}(01)$ beschreibt dann beispielsweise die minimale Gesamtfehlergröße für die Detektion des Symbols $a_\nu$ unter der Hypothese, dass $a_{\nu-1} = 0$ und $a_{\nu-2} = 1$ sein werden, und es gilt:
- $${\it \Gamma}_{\nu}(01) = {\rm Min}\big[{\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001), \hspace{0.2cm}{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101)\big] \hspace{0.05cm}.$$
In der Aufgabe 3.12 wird im Detail auf die Berechnung der Fehlergrößen (Metriken) und die Minimierung der Gesamtfehlergrößen (akkumulierten Metriken) eingegangen.
$\text{Beispiel 4:}$ Wir betrachten hier ein beispielhaftes Trellisdiagramm, das die (fehlerfreie) Detektion von folgender Symbolfolge widergibt:
- $$a_{1}=0 \hspace{0.05cm},\hspace{0.2cm} a_{2}=0 \hspace{0.05cm},\hspace{0.2cm} a_{3}=1 \hspace{0.05cm},\hspace{0.2cm} a_{4}=1 \hspace{0.05cm},\hspace{0.2cm} a_{5}=1 \hspace{0.05cm},\hspace{0.2cm} a_{6}=0 \hspace{0.05cm}, \hspace{0.05cm}\text{...}$$
Dieses vereinfachte Trellisdiagramm erlaubt folgende Aussagen:
- Alle von ${\it \Gamma}_{\nu}(00)$ bzw. ${\it \Gamma}_{\nu}(01)$ abgehende Zweige sind dem Symbol $\rm 0$ zugeordnet und blau gezeichnet. Die von den beiden oberen Zuständen abgehenden roten Zweige kennzeichnen das Symbol $\rm 1$.
- Verfolgt man die durchgehenden Pfade, so erkennt man die angegebene Folge. Da zum Zeitpunkt $\nu = 6$ nur blaue Zweige ankommen, liegen hier die ersten sechs Bit der Folge endgültig fest.
- Teilfolgen könnten aber auch bereits zu den Zeiten $\nu = 1$, $\nu = 3$ und $\nu = 4$ ausgegeben werden, da sich zu diesen Zeiten für alle vier Zustände die gleichen Teilpfade ergeben.
- Dagegen darf bei $\nu = 2$ und $\nu = 5$ nicht sofort entschieden werden. Beispielsweise ist zum Zeitpunkt $\nu = 5$ nur sicher, dass entweder $a_5 = 0$ und $a_6 = 1$ sein werden oder $a_5 = 1$ und $a_6 = 0$. Andere Kombinationen sind nicht möglich.
Fehlerwahrscheinlichkeit bei Maximum–Likelihood–Entscheidung
Die exakte Fehlerwahrscheinlichkeitsberechnung bei ML–Entscheidung (zum Beispiel mit dem Korrelations– oder dem Viterbi–Empfänger) ist sehr aufwändig. Dabei müssen
- die Differenzenergien zwischen allen möglichen Symbolfolgen $Q_i$ und $Q_{j \ne i}$ ermittelt werden, wobei die Fehlerwahrscheinlichkeit im Wesentlichen durch die minimale Differenzenergie bestimmt wird;
- auch die Einflüsse von Matched–Filter $H_{\rm MF}(f)$ und Dekorrelationsfilter $H_{\rm DF}(f)$ berücksichtigt und zusätzlich der Effektivwert $\sigma_d$ des Detektionsstörsignals bestimmt werden.
$\text{Ohne Beweis:}$ Eine einfache Näherung für die (mittlere) Fehlerwahrscheinlichkeit bei Maximum–Likelihood––Entscheidung lautet:
- $$p_{\rm ML} = {\rm Q}\left(g_{\rm max}/{\sigma_d}\right) \hspace{0.3cm}{\rm mit}\hspace{0.2cm}g_{\rm max}= {\rm Max}\hspace{0.15cm} \vert g_\nu \vert \hspace{0.05cm}.$$
Die Näherung gilt nur für binäre bipolare Signalisierung. Bei unipolarer Signalisierung ist das Argument der Q-Funktion zu halbieren.
Für die folgende Interpretation und das anschließende Beispiel wird vorausgesetzt, dass $v + 1$ Grundimpulswerte (inklusive Hauptwert) von Null verschieden sind. Dann gilt:
- Der Viterbi–Entscheider muss alle diese Grundimpulswerte berücksichtigen. Das bedeutet, dass ein Trellisdiagramm mit $2^v$ Zuständen zu bearbeiten ist.
- Voraussetzung für die Gültigkeit obiger Gleichung ist die Unkorreliertheit der Störungen am Entscheider, die durch das Dekorrelationsfilter erreicht wird.
- Für den Vergleich mit Schwellenwertentscheider $(p_{\rm SE})$ bzw. Entscheidungsrückkopplung $(p_{\rm DFE})$ wird der Störeffektivwert $\sigma_d$ als konstant vorausgesetzt.
- Die Optimierung des ML–Systems führt zu sehr schmalbandigen Filtern, da alle Impulsausläufer durch den ML–Algorithmus herausgerechnet werden können.
- Bei konstanter Rauschleistungsdichte $N_0$ (am Empfängereingang) ist somit der Störeffektivwert $\sigma_d$ (am Entscheider) beim ML–System kleiner als bei anderen Varianten.
- Das bedeutet: Der Störabstandsgewinn durch die ML–Entscheidung ist unter Umständen noch größer, als es das folgende Beispiel $($mit $\sigma_d = \rm const.)$ ausdrückt.
$\text{Beispiel 5:}$ Wir betrachten die Grundimpulswerte $g_{0} = 0.6$ und $g_{-1} = g_{+1} = 0.2 \ ( = g_1)$. Zudem gehen wir vom konstanten Störeffektivwert $\sigma_d = 0.1$ aus. Zur Vereinfachung sind alle Größen normiert.
- Bei einem Binärempfänger mit einfacher Schwellenwertentscheidung $\rm (SE)$ entsprechend dem Kapitel Fehlerwahrscheinlichkeit unter Berücksichtigung von Impulsinterferenzen ergibt sich bei bipolarer Signalisierung für die (mittlere) Fehlerwahrscheinlichkeit:
- $$p_{\rm SE} = {1}/{4}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}+\hspace{-0.02cm}2 \cdot g_{1} }{\sigma_d}\right) +{1}/{2}\cdot {\rm Q}\left(\frac{g_{0} }{\sigma_d}\right)+ {1}/{4}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}-\hspace{-0.02cm}2 \cdot g_{1} }{\sigma_d}\right) \approx {1}/{4}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}-\hspace{-0.02cm}2 \cdot g_{1} }{\sigma_d}\right) = \frac{ {\rm Q}(2)}{4}= 0.57 \% \hspace{0.05cm}.$$
- Für den Empfänger mit Entscheidungsrückkopplung $\rm (DFE)$ erhält man unter Berücksichtigung von $g_{+1} = 0$ (vollständige Kompensation des Nachläufers):
- $$p_{\rm DFE} ={1}/{2}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}+\hspace{-0.02cm}g_{-1} }{\sigma_d}\right) +{1}/{2}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}-\hspace{-0.02cm}g_{-1} }{\sigma_d}\right)\approx {1}/{2}\cdot {\rm Q}\left(\frac{g_{0}\hspace{-0.02cm}-\hspace{-0.02cm}g_{-1} }{\sigma_d}\right)=\frac{{\rm Q}(4)}{4}= 0.16 \cdot 10^{-4} \hspace{0.05cm}.$$
- Dagegen führt die Anwendung der Maximum–Likelihood–Entscheidung (mit Korrelations–Empfänger bzw. Viterbi–Empfänger) $\rm (ML)$ zur sehr viel kleineren Fehlerwahrscheinlichkeit
- $$p_{\rm ML} = {\rm Q}\left(\frac{g_{0}}{\sigma_d}\right) \approx {\rm Q}(6) = 10^{-9} \hspace{0.05cm}.$$
- Dies entspricht gegenüber den beiden anderen Systemen einem Störabstandsgewinn von ca. $3 \ \rm dB$ (gegenüber $\rm DFE$) bzw. $7.5 \ \rm dB$ (gegenüber $\rm SE$). Das Ergebnis dieser einfachen Näherung wurde durch Simulationen im Wesentlichen bestätigt.
Um den beschriebenen Viterbi–Algorithmus direkt anwenden zu können, müssen in den Gleichungen die (normierten) Grundimpulswerte $g_{0} =0.2$, $g_{-1} =0.6$ und $g_{-2} =0.2$ eingestellt werden. Eine Zeitverschiebung um Vielfache der Symboldauer $T$ gegenüber dem aus Darstellungsgründen gewählten Koordinatensystem ändert nämlich die Leistungsmerkmale der Viterbi–Entscheidung nicht.
Die Maximum–Likelihood–Fehlerwahrscheinlichkeit nach obiger Gleichung richtet sich allein nach dem größten Grundimpulswert. Dabei kann es durchaus sein, dass ein „Vorläufer” $($hier: $g_{-1} =0.6)$ größer als der Hauptwert $g_{0}$ ist. Bei Schwellenwertentscheidung würde das zu einem geschlossenen Auge führen.
$\text{Fazit:}$ Eine Maximum–Likelihood–Entscheidung ist nur bei Vorhandensein von Impulsinterferenzen von Vorteil. Bei Nyquistentzerrung (das heißt: Nur der Grundimpulswert $g_0$ ist ungleich Null) arbeitet auch der Maximum–Likelihood–Empfänger symbolweise und mit gleicher Fehlerwahrscheinlichkeit ${\rm Q}(g_0/\sigma_d)$ wie ein Empfänger mit Schwellenwertentscheidung.
Aufgaben zum Kapitel
Aufgabe 3.11: Viterbi–Empfänger und Trellisdiagramm
Aufgabe 3.11Z: Maximum-Likelihood-Fehlergrößen
Aufgabe 3.12: Trellisdiagramm für zwei Vorläufer
Aufgabe 3.13: Vergleich SWE – DFE – ML