Aufgaben:Aufgabe 3.6: Gerades und ungerades Zeitsignal: Unterschied zwischen den Versionen

Version vom 17. April 2016, 23:39 Uhr

Gerades/ungerades Zeitsignal (Aufgabe A3.6)

Gesucht ist das Spektrum $X(f)$ des nebenstehend skizzierten impulsförmigen Signals $x(t)$, das im Bereich von $–T/2$ bis $T/2$ linear von 2 V auf 4 V ansteigt und außerhalb 0 ist. Die Spektralfunktionen der unten dargestellten Signale $g(t)$ und $u(t)$ können als bekannt vorausgesetzt werden.

Die gerade, rechteckförmige Zeitfunktion $g(t)$ besitzt das Spektrum

$$G( f ) = A_g \cdot T \cdot {\mathop{\rm si}\nolimits}( {{\rm{\pi }}fT} ) \hspace{0.3cm} {\rm{mit}}\hspace{0.3cm} {\mathop{\rm si}\nolimits}( x ) = \frac[[:Vorlage:\sin ( x )]]{x}.$$

Das Spektrum der unsymmetrischen Funktion $u(t)$ lautet:

$$U( f ) = - {\rm{j}} \cdot \frac[[:Vorlage:A u \cdot T]]{{2{\rm{\pi }}fT}}\left[ {{\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( {{\rm{\pi }}fT} )} \right].$$

Verwenden Sie für die Teilaufgaben a) und b) die Signalparameter Au = 1 V und T = 1 ms. Hinweis: Lösen Sie diese Aufgabe mit Hilfe des Zuordnungssatzes in Kapitel 3.3.

Fragebogen

Musterlösung

1. a) Für f · T = 0.5 erhält man aus der angegebenen Gleichung:

$$U( {f = 0.5\;{\rm{kHz}}} ) = - {\rm{j}} \cdot \frac[[:Vorlage:A u \cdot T]]{{\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {\frac{{\rm{\pi }}}{2}} ) = - {\rm{j}} \cdot \frac{2}{{{\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u} \cdot T.$$

Der Imaginärteil ist zahlenmäßig ca. –2 · 10–4 V/Hz. Dagegen liefert die si-Funktion bei f · T = 1 den Wert 0, während der Cosinus gleich –1 ist. Damit erhält man mit Au = 1 V und T = 1 ms:

$$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{{A_{\rm u} \cdot T}}{{{\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [...] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [...] \hspace{0.15 cm}\underline{\approx \cdot 1.59 \cdot 10^{ - 4} \;{\rm{V/Hz}}}.$$

b) Eine ungerade Zeitfunktion u(t) besitzt nach dem Zuordnungssatz stets ein imaginäres und gleichzeitig ungerades Spektrum:

$$U( { - f} ) = - U( f ).$$

Mit dem Grenzübergang f → 0 folgt aus der angegebenen Gleichung

$$U( f ) = - {\rm{j}} \cdot \frac[[:Vorlage:A u \cdot T]]{{2{\rm{\pi }}fT}}\left[ {{\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( {{\rm{\pi }}fT} )} \right]$$

das Ergebnis U(f = 0). Formal könnte man dieses Ergebnis durch Anwendung der l'Hospitalschen Regel bestätigen. Wir gehen etwas pragmatischer vor. Setzen wir zum Beispiel f · T = 0.01, so erhält man:

$$U( {f \cdot T = 0.01}) &=& -{\rm{j}} \cdot \frac{{A_{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {{\mathop{\rm si}\nolimits} ( {0.01{\rm{\pi }}} ) - \cos ( {0.01{\rm{\pi }}} )} ) \\&=& - {\rm{j}} \cdot \frac{{A{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {0.999836 - 0.999507} ) \approx - {\rm{j}} \cdot 5 \cdot 10^{ - 6} \;{\rm{V/Hz}}{\rm{.}}$$

Für noch kleinere Frequenzwerte wird auch das Ergebnis immer kleiner. Schneller kommt man zum Ergebnis U(f = 0) = 0, wenn man berücksichtigt, dass das Integral über u(t) verschwindet. c) Das Signal x(t) kann in einen geraden und einen ungeraden Anteil aufgeteilt werden, die zum geraden Realteil bzw. zum ungeraden Imaginärteil von X(f) führen. Der gerade Anteil ist gleich der Funktion g(t) mit Ag = 3 V. Daraus folgt für den Spektralwert bei f · T = 0.5:

$${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {\frac{{\rm{\pi }}}{2}} ) \hspace{0.15 cm}\underline{= 1.91 \cdot 10^{ - 3} \;{\rm{V/Hz}}}{\rm{.}}$$

Der Imaginärteil ergibt sich aus der Spektralfunktion U(f) mit Au = 1 V. Dieser wurde in der Teilaufgabe a) berechnet:

$${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{= - 2 \cdot 10^{ - 4} \;{\rm{V/Hz}}}{\rm{.}}$$

@@ Zeile 2: / Zeile 2: @@
 {{quiz-Header|Buchseite=*Buch*/*Kapitel*
 }}
+[[Datei:P_ID516__Sig_A_3_6_neu.png|250px|right|Gerades/ungerades Zeitsignal (Aufgabe A3.6)]]
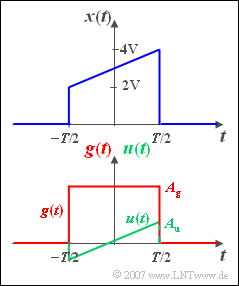
+Gesucht ist das Spektrum $X(f)$ des nebenstehend skizzierten impulsförmigen Signals $x(t)$, das im Bereich von $–T/2$ bis $T/2$ linear von 2 V auf 4 V ansteigt und außerhalb 0 ist.
+Die Spektralfunktionen der unten dargestellten Signale $g(t)$ und $u(t)$ können als bekannt vorausgesetzt werden.
+*Die gerade, rechteckförmige Zeitfunktion $g(t)$ besitzt das Spektrum
+$$G( f ) = A_g  \cdot T \cdot {\mathop{\rm si}\nolimits}( {{\rm{\pi }}fT} ) \hspace{0.3cm} {\rm{mit}}\hspace{0.3cm} {\mathop{\rm si}\nolimits}( x ) = \frac{{\sin ( x )}}{x}.$$
+*Das Spektrum der unsymmetrischen Funktion $u(t)$ lautet:
+$$U( f ) =  - {\rm{j}} \cdot \frac{{A_u  \cdot T}}{{2{\rm{\pi }}fT}}\left[ {{\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( {{\rm{\pi }}fT} )} \right].$$
+Verwenden Sie für die Teilaufgaben a) und b) die Signalparameter Au = 1 V und T = 1 ms.
+Hinweis: Lösen Sie diese Aufgabe mit Hilfe des Zuordnungssatzes in Kapitel 3.3.
 ===Fragebogen===
 <quiz display=simple>
-{Multiple-Choice Frage
+{Berechnen Sie die (rein imaginären) Spektralwerte des unsymmetrischen Signals u(t) bei den Frequenzen f = 0.5 kHz und f = 1 kHz.
-|type="[]"}
+|type="{}"}
-- Falsch
+$Im[U(f=0.5 \text{kHz}] =$ { -0.2 } mV/Hz
-+ Richtig
+$Im[U(f=1 \text{kHz}] =$ { 1.59 3% } mV/Hz
+{Wie groß ist der Spektralwert von u(t) bei der Frequenz f = 0?
+Hinweis: Lieber denken als rechnen.
+|type="{}"}
+$Im[U(f=0 \text{kHz}] =$ { 0 } mV/Hz
-{Input-Box Frage
+{Berechnen Sie unter Verwendung des Ergebnisses aus a) den Spektralwert des Signals x(t) bei der Frequenz f = 0.5 kHz.
 |type="{}"}
-<math> \alpha = </math> { 0.3 _5 }
+$Re[X(f=0.5 \text{kHz}] =$ { 1.91 3% } mV/Hz
+$Im[X(f=0.5 \text{kHz}] =$ { -0.2 } mV/Hz
@@ Zeile 20: / Zeile 41: @@
 ===Musterlösung===
 {{ML-Kopf}}
-'''1.'''  Antwort 1
+'''1.''' a)  Für f · T = 0.5 erhält man aus der angegebenen Gleichung:
+$$U( {f = 0.5\;{\rm{kHz}}} ) =  - {\rm{j}} \cdot \frac{{A_u  \cdot T}}{{\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {\frac{{\rm{\pi }}}{2}} ) =  - {\rm{j}} \cdot \frac{2}{{{\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u}  \cdot T.$$
+Der Imaginärteil ist zahlenmäßig ca. –2 · 10–4 V/Hz. Dagegen liefert die si-Funktion bei f · T = 1 den Wert 0, während der Cosinus gleich –1 ist. Damit erhält man mit Au = 1 V und T = 1 ms:
+$$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{{A_{\rm u} \cdot T}}{{{\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [...] \hspace{0.15 cm}\underline{ =  0}, \hspace{0.3 cm}{\rm Im} [...] \hspace{0.15 cm}\underline{\approx  \cdot 1.59 \cdot 10^{ - 4} \;{\rm{V/Hz}}}.$$
+b)  Eine ungerade Zeitfunktion u(t) besitzt nach dem Zuordnungssatz stets ein imaginäres und gleichzeitig ungerades Spektrum:
+$$U( { - f} ) =  - U( f ).$$
+Mit dem Grenzübergang f → 0 folgt aus der angegebenen Gleichung
+$$U( f ) =  - {\rm{j}} \cdot \frac{{A_u  \cdot T}}{{2{\rm{\pi }}fT}}\left[ {{\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( {{\rm{\pi }}fT} )} \right]$$
+das Ergebnis U(f = 0). Formal könnte man dieses Ergebnis durch Anwendung der l'Hospitalschen Regel bestätigen. Wir gehen etwas pragmatischer vor. Setzen wir zum Beispiel f · T = 0.01, so erhält man:
+$$U( {f \cdot T = 0.01}) &=& -{\rm{j}} \cdot \frac{{A_{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {{\mathop{\rm si}\nolimits} ( {0.01{\rm{\pi }}} ) - \cos ( {0.01{\rm{\pi }}} )} ) \\&=&  - {\rm{j}} \cdot \frac{{A{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {0.999836 - 0.999507} ) \approx  - {\rm{j}} \cdot 5 \cdot 10^{ - 6} \;{\rm{V/Hz}}{\rm{.}}$$
+Für noch kleinere Frequenzwerte wird auch das Ergebnis immer kleiner. Schneller kommt man zum Ergebnis U(f = 0) = 0, wenn man berücksichtigt, dass das Integral über u(t) verschwindet.
+c)  Das Signal x(t) kann in einen geraden und einen ungeraden Anteil aufgeteilt werden, die zum geraden Realteil bzw. zum ungeraden Imaginärteil von X(f) führen. Der gerade Anteil ist gleich der Funktion g(t) mit Ag = 3 V. Daraus folgt für den Spektralwert bei f · T = 0.5:
+$${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g}  \cdot T \cdot {\mathop{\rm si}\nolimits} ( {\frac{{\rm{\pi }}}{2}} ) \hspace{0.15 cm}\underline{= 1.91 \cdot 10^{ - 3} \;{\rm{V/Hz}}}{\rm{.}}$$
+Der Imaginärteil ergibt sich aus der Spektralfunktion U(f) mit Au = 1 V. Dieser wurde in der Teilaufgabe a) berechnet:
+$${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{=  - 2 \cdot 10^{ - 4} \;{\rm{V/Hz}}}{\rm{.}}$$
 {{ML-Fuß}}
 __NOEDITSECTION__
 [[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]]