Aufgaben:Aufgabe 5.2: Inverse Diskrete Fouriertransformation: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
David (Diskussion | Beiträge) |
||
| Zeile 5: | Zeile 5: | ||
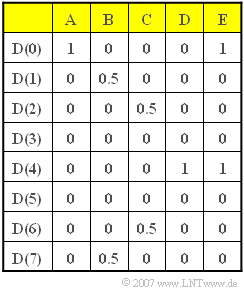
[[Datei:P_ID1138__Sig_A_5_2.png|250px|right|Verwendete Spektralkoeffizienten (Aufgabe A5.2)]] | [[Datei:P_ID1138__Sig_A_5_2.png|250px|right|Verwendete Spektralkoeffizienten (Aufgabe A5.2)]] | ||
| − | Bei der Diskreten Fouriertransformation (DFT) werden aus den N Koeffizienten d(ν) – also den Abtastwerten des Zeitsignals x(t) – die N Spektralbereichskoeffizienten D( | + | Bei der Diskreten Fouriertransformation (DFT) werden aus den N Koeffizienten $d(ν)$ – also den Abtastwerten des Zeitsignals $x(t)$ – die $N$ Spektralbereichskoeffizienten $D(\mu)$ berechnet. Mit $ν$ = 0, ... , $N$ – 1 und $\mu$ = 0, ... , $N$ – 1 gilt: |
$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} | $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} | ||
| Zeile 21: | Zeile 21: | ||
D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | ||
| − | In dieser Aufgabe sollen für verschiedene Beispielfolgen D( | + | In dieser Aufgabe sollen für verschiedene Beispielfolgen $D(\mu)$ – die in obiger Tabelle mit „A”, ... , „E” bezeichnet sind – die Zeitkoeffizienten $d(ν)$ ermittelt werden. Es gilt somit stets $N$ = 8. |
Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.2. Diese können Sie sich auch mit folgendem Interaktionsmodul verdeutlichen: | Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.2. Diese können Sie sich auch mit folgendem Interaktionsmodul verdeutlichen: | ||
Diskrete Fouriertransformation | Diskrete Fouriertransformation | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lauten die Zeitkoeffizienten d(ν) für die D( | + | {Wie lauten die Zeitkoeffizienten $d(ν)$ für die $D(\mu)$–Werte von Spalte A? |
|type="{}"} | |type="{}"} | ||
$D(\mu )$ gemäß A: $d(0) =$ { 1 } | $D(\mu )$ gemäß A: $d(0) =$ { 1 } | ||
$D(\mu )$ gemäß A: $d(1) =$ { 1 } | $D(\mu )$ gemäß A: $d(1) =$ { 1 } | ||
| − | {Wie lauten die Zeitkoeffizienten d(ν) für die D( | + | {Wie lauten die Zeitkoeffizienten $d(ν)$ für die $D(\mu)$–Werte von Spalte B? |
|type="{}"} | |type="{}"} | ||
$D(\mu )$ gemäß B: $d(0) =$ { 1 } | $D(\mu )$ gemäß B: $d(0) =$ { 1 } | ||
$D(\mu )$ gemäß B: $d(1) =$ { 0.707 3% } | $D(\mu )$ gemäß B: $d(1) =$ { 0.707 3% } | ||
| − | {Wie lauten die Zeitkoeffizienten d(ν) für die D( | + | {Wie lauten die Zeitkoeffizienten $d(ν)$ für die $D(\mu)$ –Werte von Spalte C? |
|type="{}"} | |type="{}"} | ||
$D(\mu )$ gemäß C: $d(0) =$ { 1 } | $D(\mu )$ gemäß C: $d(0) =$ { 1 } | ||
$D(\mu )$ gemäß C: $d(1) =$ { 0 } | $D(\mu )$ gemäß C: $d(1) =$ { 0 } | ||
| − | {Wie lauten die Zeitkoeffizienten d(ν) für die D( | + | {Wie lauten die Zeitkoeffizienten $d(ν)$ für die $D(\mu)$–Werte von Spalte D? |
|type="{}"} | |type="{}"} | ||
$D(\mu )$ gemäß D: $d(0) =$ { 1 } | $D(\mu )$ gemäß D: $d(0) =$ { 1 } | ||
$D(\mu )$ gemäß D: $d(1) =$ { -1 } | $D(\mu )$ gemäß D: $d(1) =$ { -1 } | ||
| − | {Wie lauten die Zeitkoeffizienten d(ν) für die D( | + | {Wie lauten die Zeitkoeffizienten $d(ν)$ für die $D(\mu)$–Wertevon Spalte E? |
|type="{}"} | |type="{}"} | ||
$D(\mu )$ gemäß A: $d(0) =$ { 2 } | $D(\mu )$ gemäß A: $d(0) =$ { 2 } | ||
| Zeile 58: | Zeile 59: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Aus der IDFT–Gleichung wird mit $D(\mu)$ = 0 für $\mu \approx$ 0: |
$$d(\nu) = D(0) \cdot w^0 = D(0) =1\hspace{0.5cm}(0 \le \nu \le 7)$$ | $$d(\nu) = D(0) \cdot w^0 = D(0) =1\hspace{0.5cm}(0 \le \nu \le 7)$$ | ||
| Zeile 69: | Zeile 70: | ||
X(f) = {\delta}(f) \hspace{0.05cm}.$$ | X(f) = {\delta}(f) \hspace{0.05cm}.$$ | ||
| − | + | '''2.''' Alle Spektralkoeffizienten sind 0 mit Ausnahme von $D_1$ = $D_7$ = 0.5. Daraus folgt für 0 ≤ $ν$ ≤ 7: | |
$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} | $$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} | ||
| Zeile 84: | Zeile 85: | ||
X(f) = \frac {1}{2} \cdot {\delta}(f + f_{\rm A}) + \frac {1}{2} \cdot {\delta}(f - f_{\rm A}) \hspace{0.05cm},$$ | X(f) = \frac {1}{2} \cdot {\delta}(f + f_{\rm A}) + \frac {1}{2} \cdot {\delta}(f - f_{\rm A}) \hspace{0.05cm},$$ | ||
| − | wobei | + | wobei $f_A$ die kleinste in der DFT darstellbare Frequenz bezeichnet. |
| − | + | ||
| + | '''3.''' Gegenüber Aufgabe 2) ist nun die Frequenz doppelt so groß, nämlich 2 · $f_A$ anstelle von $f_A$: | ||
$$x(t) = \cos(2 \pi \cdot (2f_{\rm A}) \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} | $$x(t) = \cos(2 \pi \cdot (2f_{\rm A}) \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} | ||
X(f) = \frac {1}{2} \cdot {\delta}(f + 2f_{\rm A}) + \frac {1}{2} \cdot {\delta}(f - 2f_{\rm A}) \hspace{0.05cm},$$ | X(f) = \frac {1}{2} \cdot {\delta}(f + 2f_{\rm A}) + \frac {1}{2} \cdot {\delta}(f - 2f_{\rm A}) \hspace{0.05cm},$$ | ||
| − | Damit beschreibt die Folge | + | Damit beschreibt die Folge 〈 $d(ν)$〉 zwei Perioden der Cosinusschwingung, und es gilt für 0 ≤ $ν$ ≤ 7: |
| − | $$d(\nu) & = | + | $$ d(\nu) & = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left({\pi}/{2} \cdot \nu \right)\\ \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{d(0) = 1, \hspace{0.2cm}d(1) = 0} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | '''4.''' Durch eine weitere Verdoppelung der Cosinusfrequenz auf 4fA kommt man schließlich zur zeitkontinuierlichen Fourierkorrespondenz | |
$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left(\pi \cdot \nu \right) | $$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left(\pi \cdot \nu \right) | ||
| Zeile 106: | Zeile 108: | ||
Zu beachten ist, dass die beiden Diracfunktionen in der zeitdiskreten Darstellung aufgrund der Periodizität zusammenfallen. Das heißt: Die Koeffizienten D(4) = 0.5 und D(-4) = 0.5 ergeben zusammen D(4) = 1. | Zu beachten ist, dass die beiden Diracfunktionen in der zeitdiskreten Darstellung aufgrund der Periodizität zusammenfallen. Das heißt: Die Koeffizienten D(4) = 0.5 und D(-4) = 0.5 ergeben zusammen D(4) = 1. | ||
| − | + | ||
| + | '''5.''' Die Diskrete Fouriertransformation ist ebenfalls linear. Deshalb ist das Superpositionsprinzip weiterhin anwendbar. Die Koeffizienten D(μ) aus Spalte E ergeben sich als die Summen der Spalten A und D. Deshalb wird aus der alternierenden Folge 〈d(ν)〉 entsprechend Teilaufgabe d) die um 1 nach oben verschobene Folge: | ||
$$ \hspace{0.15 cm}\underline{d(0) =d(2) =d(4) =d(6)= 2}, \hspace{0.2cm}\hspace{0.15 cm}\underline{d(1) =d(3) =d(5) =d(7) = 0} | $$ \hspace{0.15 cm}\underline{d(0) =d(2) =d(4) =d(6)= 2}, \hspace{0.2cm}\hspace{0.15 cm}\underline{d(1) =d(3) =d(5) =d(7) = 0} | ||
Version vom 20. April 2016, 13:44 Uhr
Bei der Diskreten Fouriertransformation (DFT) werden aus den N Koeffizienten $d(ν)$ – also den Abtastwerten des Zeitsignals $x(t)$ – die $N$ Spektralbereichskoeffizienten $D(\mu)$ berechnet. Mit $ν$ = 0, ... , $N$ – 1 und $\mu$ = 0, ... , $N$ – 1 gilt:
$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
Hierbei bezeichnet w den komplexen Drehfaktor:
$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
Für die Inverse Diskrete Fouriertransformation (IDFT) gilt entsprechend ⇒ „Umkehrfunktion” der DFT:
$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
In dieser Aufgabe sollen für verschiedene Beispielfolgen $D(\mu)$ – die in obiger Tabelle mit „A”, ... , „E” bezeichnet sind – die Zeitkoeffizienten $d(ν)$ ermittelt werden. Es gilt somit stets $N$ = 8. Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.2. Diese können Sie sich auch mit folgendem Interaktionsmodul verdeutlichen: Diskrete Fouriertransformation
Fragebogen
Musterlösung
$$d(\nu) = D(0) \cdot w^0 = D(0) =1\hspace{0.5cm}(0 \le \nu \le 7)$$
$$\Rightarrow\hspace{0.5cm}\hspace{0.15 cm}\underline{d(0) = d(1) = 1}.$$
Dieser Parametersatz beschreibt die diskrete Form der Fourierkorrespondenz des Gleichsignals:
$$x(t) = 1 \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = {\delta}(f) \hspace{0.05cm}.$$
2. Alle Spektralkoeffizienten sind 0 mit Ausnahme von $D_1$ = $D_7$ = 0.5. Daraus folgt für 0 ≤ $ν$ ≤ 7:
$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} \hspace{0.05cm}.$$
Aufgrund der Periodizität gilt aber auch:
$$d(\nu) & = & 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left({\pi}/{4} \cdot \nu \right)\\ & \Rightarrow & \hspace{0.3cm}\hspace{0.15 cm}\underline{d(0) = 1}, \hspace{0.2cm}\hspace{0.15 cm}\underline{d(1) = {1}/{\sqrt{2}} \approx 0.707} \hspace{0.05cm}.$$
Es handelt sich also um das zeitdiskrete Äquivalent zu
$$x(t) = \cos(2 \pi \cdot f_{\rm A} \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = \frac {1}{2} \cdot {\delta}(f + f_{\rm A}) + \frac {1}{2} \cdot {\delta}(f - f_{\rm A}) \hspace{0.05cm},$$
wobei $f_A$ die kleinste in der DFT darstellbare Frequenz bezeichnet.
3. Gegenüber Aufgabe 2) ist nun die Frequenz doppelt so groß, nämlich 2 · $f_A$ anstelle von $f_A$:
$$x(t) = \cos(2 \pi \cdot (2f_{\rm A}) \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = \frac {1}{2} \cdot {\delta}(f + 2f_{\rm A}) + \frac {1}{2} \cdot {\delta}(f - 2f_{\rm A}) \hspace{0.05cm},$$
Damit beschreibt die Folge 〈 $d(ν)$〉 zwei Perioden der Cosinusschwingung, und es gilt für 0 ≤ $ν$ ≤ 7:
$$ d(\nu) & = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left({\pi}/{2} \cdot \nu \right)\\ \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{d(0) = 1, \hspace{0.2cm}d(1) = 0} \hspace{0.05cm}.$$
4. Durch eine weitere Verdoppelung der Cosinusfrequenz auf 4fA kommt man schließlich zur zeitkontinuierlichen Fourierkorrespondenz
$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left(\pi \cdot \nu \right) \hspace{0.05cm}$$
und damit zu den Zeitkoeffizienten
$$d(0) =d(2) =d(4) =d(6) \hspace{0.15 cm}\underline{= +1}, \hspace{0.2cm}d(1) =d(3) =d(5) =d(7) \hspace{0.15 cm}\underline{= -1} \hspace{0.05cm}.$$
Zu beachten ist, dass die beiden Diracfunktionen in der zeitdiskreten Darstellung aufgrund der Periodizität zusammenfallen. Das heißt: Die Koeffizienten D(4) = 0.5 und D(-4) = 0.5 ergeben zusammen D(4) = 1.
5. Die Diskrete Fouriertransformation ist ebenfalls linear. Deshalb ist das Superpositionsprinzip weiterhin anwendbar. Die Koeffizienten D(μ) aus Spalte E ergeben sich als die Summen der Spalten A und D. Deshalb wird aus der alternierenden Folge 〈d(ν)〉 entsprechend Teilaufgabe d) die um 1 nach oben verschobene Folge:
$$ \hspace{0.15 cm}\underline{d(0) =d(2) =d(4) =d(6)= 2}, \hspace{0.2cm}\hspace{0.15 cm}\underline{d(1) =d(3) =d(5) =d(7) = 0} \hspace{0.05cm}.$$