Lineare zeitinvariante Systeme/Klassifizierung der Verzerrungen: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 1: | Zeile 1: | ||
| − | + | {{FirstPage}} | |
| − | {{Header | + | {{Header| |
| − | + | Untermenü=Signalverzerrungen und Entzerrung | |
| − | |||
|Nächste Seite=Nichtlineare Verzerrungen | |Nächste Seite=Nichtlineare Verzerrungen | ||
}} | }} | ||
| + | ==Voraussetzungen für Kapitel 2== | ||
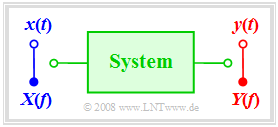
| + | Wir betrachten im Folgenden ein System, an dessen Eingang das Signal $x(t)$ mit zugehörigem Spektrum $X(f)$ anliegt. Das Ausgangssignal bezeichnen wir mit $y(t)$ und dessen Spektrum mit $Y(f).$ | ||
| + | [[Datei:P_ID873__LZI_T_2_1_S1_neu.png|400px | Beschreibung eines linearen Systems]] | ||
| + | |||
| + | |||
| + | Der mit „System” bezeichnete Block kann ein Teil einer elektrischen Schaltung sein oder ein komplettes Übertragungssystem, bestehend aus Sender, Kanal und Empfänger. | ||
| + | |||
| + | |||
| + | Für das gesamte Kapitel 2 soll gelten: | ||
| + | *Das System sei zeitinvariant. Führt das Eingangssignal $x(t)$ zum Signal $y(t)$, so wird ein späteres Eingangssignal gleicher Form, nämlich $x(t – t_0)$, das Signal $y(t – t_0)$ zur Folge haben. | ||
| + | *Es werden keine Rauschprozesse betrachtet, die bei realen Systemen stets vorhanden sind. Zur Beschreibung dieser Phänomene wird auf das Buch „Stochastische Signaltheorie” verwiesen. | ||
| + | *Es werden keine Detailkenntnisse über das System vorausgesetzt. Alle Systemeigenschaften werden im Folgenden allein aus den Signalen $x(t)$ und $y(t)$ bzw. deren Spektren abgeleitet. | ||
| + | Insbesondere seien vorerst keine Festlegungen hinsichtlich der Linearität gegeben. Das „System” kann linear (Voraussetzung für die Anwendung des Superpositionsprinzips) oder nichtlinear sein. | ||
| + | *Aus einem einzigen Testsignal $x(t)$ und dessen Antwort $y(t)$ sind nicht alle Systemeigenschaften erkennbar. Daher müssen ausreichend viele Testsignale zur Bewertung herangezogen werden. | ||
| + | |||
| + | Nachfolgend werden wir solche Systeme näher klassifizieren. | ||
| − | |||
Version vom 5. Mai 2016, 10:39 Uhr
- [[Lineare zeitinvariante Systeme/{{{Vorherige Seite}}} | Vorherige Seite]]
- [[Lineare zeitinvariante Systeme/{{{Vorherige Seite}}} | Vorherige Seite]]
Voraussetzungen für Kapitel 2
Wir betrachten im Folgenden ein System, an dessen Eingang das Signal $x(t)$ mit zugehörigem Spektrum $X(f)$ anliegt. Das Ausgangssignal bezeichnen wir mit $y(t)$ und dessen Spektrum mit $Y(f).$
Der mit „System” bezeichnete Block kann ein Teil einer elektrischen Schaltung sein oder ein komplettes Übertragungssystem, bestehend aus Sender, Kanal und Empfänger.
Für das gesamte Kapitel 2 soll gelten:
- Das System sei zeitinvariant. Führt das Eingangssignal $x(t)$ zum Signal $y(t)$, so wird ein späteres Eingangssignal gleicher Form, nämlich $x(t – t_0)$, das Signal $y(t – t_0)$ zur Folge haben.
- Es werden keine Rauschprozesse betrachtet, die bei realen Systemen stets vorhanden sind. Zur Beschreibung dieser Phänomene wird auf das Buch „Stochastische Signaltheorie” verwiesen.
- Es werden keine Detailkenntnisse über das System vorausgesetzt. Alle Systemeigenschaften werden im Folgenden allein aus den Signalen $x(t)$ und $y(t)$ bzw. deren Spektren abgeleitet.
Insbesondere seien vorerst keine Festlegungen hinsichtlich der Linearität gegeben. Das „System” kann linear (Voraussetzung für die Anwendung des Superpositionsprinzips) oder nichtlinear sein.
- Aus einem einzigen Testsignal $x(t)$ und dessen Antwort $y(t)$ sind nicht alle Systemeigenschaften erkennbar. Daher müssen ausreichend viele Testsignale zur Bewertung herangezogen werden.
Nachfolgend werden wir solche Systeme näher klassifizieren.