Stochastische Signaltheorie/Binomialverteilung: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Diskrete Zufallsgrößen |Vorherige Seite=Momente einer diskreten Zufallsgröße |Nächste Seite=Poissonverteilung }} ==Allgemeine Besch…“) |
|||
| Zeile 36: | Zeile 36: | ||
| + | Mit nachfolgendem Berechnungsmodul können Sie die Binomialwahrscheinlichkeiten auch für andere Parameterwerte $I$ und $p$ ermitteln: | ||
| + | Ereigniswahrscheinlichkeiten der Binomialverteilung | ||
| + | |||
| + | |||
| + | ''Weitere Hinweise:'' | ||
| + | *Für sehr große Werte von $I$ kann die Binomialverteilung durch die im nächsten Abschnitt beschriebene Poissonverteilung angenähert werden. | ||
| + | *Ist gleichzeitig das Produkt $I · p$ sehr viel größer als 1, so geht nach dem Grenzwertsatz von de Moivre-Laplace die Poissonverteilung (und damit auch die Binomialverteilung) in eine diskrete Gaußverteilung über. | ||
| + | |||
| + | ==Beispiel „Blockfehlerwahrscheinlichkeit”== | ||
| + | {{Beispiel}} | ||
| + | Überträgt man jeweils Blöcke von $I =$ 10 Binärsymbolen über einen Kanal, der mit der Wahrscheinlichkeit $p =$ 0.01 das Symbol verfälscht $(e_i = 1)$ und entsprechend mit der Wahrscheinlichkeit $1 – p = 0.99$ das Symbol unverfälscht überträgt $(e_i = 0)$, so gilt für die neue Zufallsgröße $f$ (Fehler pro Block): | ||
| + | $$f=\sum_{i=1}^{I}e_i.$$ | ||
| + | |||
| + | Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen 0 (kein Symbol verfälscht) und $I$ (alle Symbole falsch) annehmen; die entsprechenden Wahrscheinlichkeiten sind $p_μ$. | ||
| + | *Der Fall, dass alle $I$ Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.99^{10} ≈ 0.9044$ ein. Dies ergibt sich auch aus der Binomialformel für $μ =$ 0 unter Berücksichtigung der Definition „10 über 0“ = 1. | ||
| + | *Ein einziger Symbolfehler $(f = 1)$ tritt mit folgender Wahrscheinlichkeit auf: | ||
| + | $$p_1 = \rm 10\cdot 0.01\cdot 0.99^9\approx 0.0914.$$ | ||
| + | Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau „10 über 1“ = 10 Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und neun richtig übertragen werden müssen, wenn $f =$ 1 gelten soll. | ||
| + | *Für $f =$ 2 gibt es deutlich mehr Kombinationen, nämlich „10 über 2“ = 45, und man erhält | ||
| + | $$p_2 = \rm 45\cdot 0.01^2\cdot 0.99^8\approx 0.0041.$$ | ||
| + | |||
| + | |||
| + | Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit | ||
| + | $$p_{\rm R} = \it p_{\rm 3}+...+\it p_{\rm 10}\approx \rm 10^{-4},$$ | ||
| + | oder | ||
| + | $$p_{\rm R} = \rm 1-\it p_{\rm 0}-\it p_{\rm 1}-p_{\rm 2}\approx \rm 10^{-4}.$$ | ||
| + | |||
| + | Man erkennt, dass die zweite Berechnungsmöglichkeit über das Komplement schneller zum Ziel führt. Man könnte aber auch berücksichtigen, dass bei diesen Zahlenwerten $p_{\rm R} ≈ p_3$ gilt. | ||
Version vom 26. Mai 2016, 19:34 Uhr
Allgemeine Beschreibung der Binomialverteilung
Die Binomialverteilung stellt einen wichtigen Sonderfall für die Auftrittswahrscheinlichkeiten einer diskreten Zufallsgröße dar.
Zur Herleitung der Binomialverteilung gehen wir davon aus, dass $I$ binäre und statistisch voneinander unabhängige Zufallsgrößen $b_i$ den Wert „1” mit der Wahrscheinlichkeit Pr( $b_i =$ 0) $= p$ und den Wert „0” mit der Wahrscheinlichkeit Pr( $b_i =$ 1) $=$ 1 – $p$ annehmen kann. Dann ist die Summe $$z=\sum_{i=1}^{I}b_i$$ ebenfalls eine diskrete Zufallsgröße mit dem Symbolvorrat {0, 1, 2, ... , $I$}, die man als binomialverteilt bezeichnet. Der Symbolumfang beträgt somit $M = I + 1.$
Die Binomialverteilung findet in der Nachrichtentechnik ebenso wie in anderen Disziplinen mannigfaltige Anwendungen. Sie
- beschreibt die Verteilung von Ausschussstücken in der statistischen Qualitätskontrolle,
- erlaubt die Berechnung der Restfehlerwahrscheinlichkeit bei blockweiser Codierung.
Die per Simulation gewonnene Bitfehlerquote eines digitalen Übertragungssystems ist im Grunde genommen ebenfalls eine binomialverteilte Zufallsgröße.
Wahrscheinlichkeiten der Binomialverteilung
Für die Wahrscheinlichkeiten der Binomialverteilung gilt mit $μ = 0, ... , I:$ $$p_\mu = \rm Pr(\it z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$ Der erste Term gibt hierbei die Anzahl der Kombinationen („ $I$ über $μ$”) an: $${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{I\cdot (I- \rm 1)\cdot ...\cdot (\it I-\mu+ \rm 1)}{\rm 1\cdot \rm 2\cdot...\cdot \it \mu}.$$
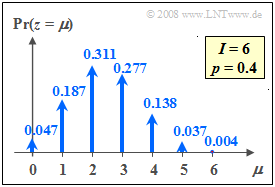
Die Grafik zeigt die Wahrscheinlichkeiten der Binomialverteilung sind für $I =$ 6 und $p =$ 0.4.
Für $I =$ 6 und $p =$ 0.5 ergeben sich die folgenden symmetrischen Binomialwahrscheinlichkeiten: $$\begin{align*}{\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}0) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}6)\hspace{-0.05cm} =\hspace{-0.05cm} 1/64\hspace{-0.05cm} = \hspace{-0.05cm}0.015625 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}1) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}5) \hspace{-0.05cm}= \hspace{-0.05cm}6/64 \hspace{-0.05cm}=\hspace{-0.05cm} 0.09375,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}2) & = {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}4)\hspace{-0.05cm} = \hspace{-0.05cm}15/64 \hspace{-0.05cm}= \hspace{-0.05cm}0.234375 ,\\ {\rm Pr}(z\hspace{-0.05cm} =\hspace{-0.05cm}3) & = 20/64 \hspace{-0.05cm}= \hspace{-0.05cm} 0.3125 \hspace{0.05cm}.\end{align*}$$
Mit nachfolgendem Berechnungsmodul können Sie die Binomialwahrscheinlichkeiten auch für andere Parameterwerte $I$ und $p$ ermitteln:
Ereigniswahrscheinlichkeiten der Binomialverteilung
Weitere Hinweise:
- Für sehr große Werte von $I$ kann die Binomialverteilung durch die im nächsten Abschnitt beschriebene Poissonverteilung angenähert werden.
- Ist gleichzeitig das Produkt $I · p$ sehr viel größer als 1, so geht nach dem Grenzwertsatz von de Moivre-Laplace die Poissonverteilung (und damit auch die Binomialverteilung) in eine diskrete Gaußverteilung über.
Beispiel „Blockfehlerwahrscheinlichkeit”
Überträgt man jeweils Blöcke von $I =$ 10 Binärsymbolen über einen Kanal, der mit der Wahrscheinlichkeit $p =$ 0.01 das Symbol verfälscht $(e_i = 1)$ und entsprechend mit der Wahrscheinlichkeit $1 – p = 0.99$ das Symbol unverfälscht überträgt $(e_i = 0)$, so gilt für die neue Zufallsgröße $f$ (Fehler pro Block): $$f=\sum_{i=1}^{I}e_i.$$
Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen 0 (kein Symbol verfälscht) und $I$ (alle Symbole falsch) annehmen; die entsprechenden Wahrscheinlichkeiten sind $p_μ$.
- Der Fall, dass alle $I$ Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.99^{10} ≈ 0.9044$ ein. Dies ergibt sich auch aus der Binomialformel für $μ =$ 0 unter Berücksichtigung der Definition „10 über 0“ = 1.
- Ein einziger Symbolfehler $(f = 1)$ tritt mit folgender Wahrscheinlichkeit auf:
$$p_1 = \rm 10\cdot 0.01\cdot 0.99^9\approx 0.0914.$$ Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau „10 über 1“ = 10 Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und neun richtig übertragen werden müssen, wenn $f =$ 1 gelten soll.
- Für $f =$ 2 gibt es deutlich mehr Kombinationen, nämlich „10 über 2“ = 45, und man erhält
$$p_2 = \rm 45\cdot 0.01^2\cdot 0.99^8\approx 0.0041.$$
Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit
$$p_{\rm R} = \it p_{\rm 3}+...+\it p_{\rm 10}\approx \rm 10^{-4},$$
oder
$$p_{\rm R} = \rm 1-\it p_{\rm 0}-\it p_{\rm 1}-p_{\rm 2}\approx \rm 10^{-4}.$$
Man erkennt, dass die zweite Berechnungsmöglichkeit über das Komplement schneller zum Ziel führt. Man könnte aber auch berücksichtigen, dass bei diesen Zahlenwerten $p_{\rm R} ≈ p_3$ gilt.