Modulationsverfahren/Zweiseitenband-Amplitudenmodulation: Unterschied zwischen den Versionen
| Zeile 88: | Zeile 88: | ||
| + | [[Datei:P_ID979__Mod_T_2_1_S3b_ganz_neu.png | Signale zur Verdeutlichung des Ringmodulators]] | ||
| + | |||
| + | |||
| + | Man erkennt deutliche Unterschiede, die sich jedoch auf einfache Weise kompensieren lassen: | ||
| + | *Die Fourierreihendarstellung des periodischen Rechtecksignals $z_{\rm R}(t)$ lautet: | ||
| + | $$z_{\rm R}(t) = \frac{4}{\pi} \cdot \cos(\omega_{\rm T}\cdot t)-\frac{4}{3\pi} \cdot \cos(3\omega_{\rm T}\cdot t) +\frac{4}{5\pi} \cdot \cos(5\omega_{\rm T}\cdot t)- ...$$ | ||
| + | *Die dazugehörige Spektralfunktion besteht demnach aus Diraclinien bei $±f_{\rm T}, ±3f_{\rm T}, ±5f_{\rm T}$ usw. Die Faltung mit $Q(f)$ führt zu der Spektralfunktion (der Index steht für „Ringmodulator”): | ||
| + | $$S_{\rm RM}(f) = \frac{2}{\pi} \cdot Q (f \pm f_{\rm T})-\frac{2}{3\pi} \cdot Q (f \pm 3f_{\rm | ||
| + | T})+\frac{2}{5\pi} \cdot Q (f \pm 5f_{\rm T}) - ... \hspace{0.05cm}.$$ | ||
| + | *Daraus ist ersichtlich, dass durch eine geeignete Bandbegrenzung (zum Beispiel auf $±2f_{\rm T})$ und eine Dämpfung mit π/4 ≈ 0.785 das bekannte ZSB–AM–Spektrum gewonnen werden kann: | ||
| + | $$S(f) = \frac{1}{2} \cdot Q (f \pm f_{\rm T})\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | Bei diesen Überlegungen ist zu berücksichtigen, dass stets $B_{\rm NF} << f_{\rm T}$ angenommen werden kann. | ||
| + | |||
| + | ==AM-Signale und -Spektren bei harmonischen Signalen (1)== | ||
| + | Nun soll der für Testzwecke wichtige Sonderfall betrachtet werden, dass nicht nur das Trägersignal $z(t)$, sondern auch das zu modulierende Nachrichtensignal $q(t)$ eine harmonische Schwingung ist: | ||
| + | $$\begin{align*}q(t) & = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}, \\ z(t) & = \hspace{0.15cm}1 \hspace{0.13cm} \cdot \hspace{0.1cm}\cos(\omega_{\rm T} \cdot t + \phi_{\rm T})\hspace{0.05cm}.\end{align*}$$ | ||
| + | |||
| + | |||
| + | Beachten Sie bitte die Anmerkungen zur Nomenklatur. Aufgrund der Pluszeichen in obigen Gleichungen sind Sinusschwingungen mit $ϕ_{\rm N} =$ – 90° bzw. $ϕ_{\rm T} =$ – 90° parametrisiert. | ||
| + | |||
| + | |||
| + | Damit lautet die Gleichung für das modulierte Signal: | ||
| + | $$s(t) = q(t) \cdot z(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} t + \phi_{\rm | ||
| + | N})\cdot \cos(\omega_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$ | ||
| + | |||
| + | Diese kann mit Hilfe des Additionstheorems der Trigonometrie umgeformt werden: | ||
| + | $$\begin{align*}s(t) & = \frac{A_{\rm N}}{2} \cdot \cos\left((\omega_{\rm T} +\omega_{\rm N})\cdot t + \phi_{\rm T}+ \phi_{\rm N}\right)\\ & + \frac{A_{\rm N}}{2} \cdot \cos\left((\omega_{\rm T} -\omega_{\rm N})\cdot t + \phi_{\rm T}- \phi_{\rm N}\right)\hspace{0.05cm}.\end{align*}$$ | ||
| + | |||
| + | Bei cosinusförmigen Signalen $(ϕ_{\rm T} = ϕ_{\rm N} = 0)$ vereinfacht sich diese Gleichung zu | ||
| + | $$s(t) = \frac{A_{\rm N}}{2} \cdot \cos\left((\omega_{\rm T}+\omega_{\rm N})\cdot t\right) + \frac{A_{\rm N}}{2} \cdot \cos\left((\omega_{\rm T} -\omega_{\rm N})\cdot t \right)\hspace{0.05cm}.$$ | ||
| + | |||
| + | Durch Fouriertransformation kommt man zur Spektralfunktion: | ||
| + | $$\begin{align*}S(f) & = \frac{A_{\rm N}}{4} \cdot \left[\delta ( f - f_{\rm T} - f_{\rm | ||
| + | N})+\delta ( f + f_{\rm T} + f_{\rm N})\right] + \\ & + \frac{A_{\rm N}}{4} \cdot \left[ \delta ( f - f_{\rm T}+ f_{\rm N})+\delta ( f+ f_{\rm T} - f_{\rm N} ) \right]\hspace{0.05cm}.\end{align*}$$ | ||
| + | |||
| + | |||
| + | Dieses Ergebnis, zu dem man auch über die Faltung gekommen wäre, besagt: | ||
| + | *Das Spektrum besteht aus vier Diraclinien bei den Frequenzen $±(f_{\rm T} + f_{\rm N})$ und $±(f_{\rm T} – f_{\rm N})$, wobei in beiden Klammerausdrücken die erste Diracfunktion diejenige bei positiver Frequenz angibt. | ||
| + | *Die Gewichte aller Diracfunktionen sind gleich und jeweils $A_{\rm N}/4$. Die Summe dieser Gewichte – also das Integral über $S(f)$ – ist entsprechend der Theorie gleich dem Signalwert $s(t = 0) = A_{\rm N}$. | ||
| + | *Die Diraclinien bleiben auch für $ϕ_{\rm T}$ ≠ 0 und/oder $ϕ_{\rm N}$ ≠ 0 bei den gleichen Frequenzen erhalten. Zu den Gewichten $A_{\rm N}/4$ müssen dann jedoch komplexe Drehfaktoren hinzugefügt werden. | ||
| + | |||
| + | ==AM-Signale und -Spektren bei harmonischen Signalen (2)== | ||
| + | {{Beispiel}} | ||
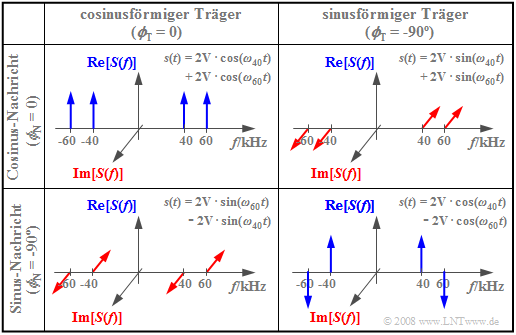
| + | Die nachfolgende Grafik zeigt die Spektralfunktionen $S(f)$ für unterschiedliche Werte von $ϕ_{\rm T}$ bzw. $ϕ_{\rm N}$. Die weiteren Parameter sind zu $f_{\rm T} =$ 50 kHz, $f_{\rm N} =$ 10 kHz und $A_{\rm N} =$ 4 V vorausgesetzt. Die Beträge aller Diraclinien sind somit $A_{\rm N}/4 =$ 1 V. | ||
| + | |||
| + | |||
| + | [[Datei:P_ID980__Mod_T_2_1_S4.png | Beispielspektren der ZSB–AM]] | ||
| + | |||
| + | |||
| + | Das linke obere Bild zeigt den auf der letzten Seite besprochenen Fall mit cosinusförmigem Träger und cosinusförmigem Nachrichtensignal. Somit setzt sich das amplitudenmodulierte Signal $s(t)$ aus zwei Cosinusschwingungen mit $ω_{60} =$ 2 π · 60 kHz und $ω_{40} =$ 2 π · 40 kHz zusammen. | ||
| + | |||
| + | |||
| + | Bei den drei anderen Konstellationen ist zumindest eines der Signale $q(t)$ bzw. $z(t)$ sinusförmig, so dass stets $s(0) = q(0) · z(0) =$ 0 ist. Somit ergeben sich bei diesen Spektralfunktionen die Summe der vier Impulsgewichte jeweils zu 0. | ||
| + | |||
| + | |||
| + | Das rechte untere Bild beschreibt $s(t) = A_{\rm N} · \sin(ω_{\rm N} t) · \sin(ω_{\rm T}t)$. Die Multiplikation zweier ungerader Funktionen ergibt die gerade Funktion $s(t)$ und damit ein reelles Spektrum $S(f)$. Dagegen führen die beiden anderen Konstellationen jeweils zu imaginären Spektralfunktionen. | ||
| + | {{end}} | ||
Version vom 14. Juni 2016, 19:40 Uhr
Inhaltsverzeichnis
Beschreibung im Frequenzbereich (1)
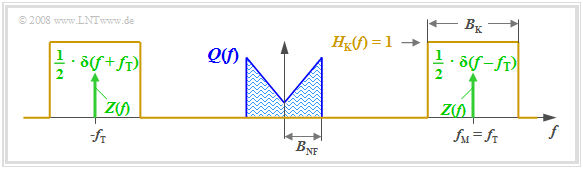
Wir betrachten die folgende Aufgabenstellung: Ein Nachrichtensignal $q(t)$, dessen Spektrum $Q(f)$ auf den Bereich $\pm B_{\rm NF}$ bandbegrenzt ist, soll mit Hilfe einer harmonischen Schwingung der Frequenz $f_{\rm T}$, die wir im Weiteren als Trägersignal $z(t)$ bezeichnen, in einen höherfrequenten Bereich verschoben werden, in dem der Kanalfrequenzgang $H_{\rm K}(f)$ günstige Eigenschaften aufweist.
Die Grafik verdeutlicht die Aufgabenstellung, wobei folgende vereinfachende Annahmen getroffen sind:
- Das gezeichnete Spektrum $Q(f)$ ist hier schematisch zu verstehen. Es besagt, dass in $q(t)$ nur Spektralanteile im Bereich $|f| ≤ B_{\rm NF}$ enthalten sind. $Q(f)$ könnte auch ein Linienspektrum sein.
- Der Kanal sei in einem Bereich der Bandbreite $B_{\rm K}$ um die Frequenz $f_{\rm M}$ ideal, das heißt, es gelte $H_{\rm K}(f) =$ 1 für $|f – f_{\rm M}| ≤ B_{\rm K}/2.$ Rauschstörungen werden vorerst nicht betrachtet.
- Das Trägersignal sei cosinusförmig (Phase $ϕ_T =$ 0) und besitze die Amplitude $A_{\rm T} =$ 1 (ohne Einheit). Die Trägerfrequenz $f_{\rm T}$ sei gleich der Mittenfrequenz des Übertragungsbandes.
- Das Spektrum des Trägersignals $z(t) = \cos(ω_{\rm T} · t)$ lautet somit (in der Grafik grün eingezeichnet):
$$Z(f) = \frac{1}{2} \cdot \delta (f + f_{\rm T})+\frac{1}{2} \cdot \delta (f - f_{\rm T})\hspace{0.05cm}.$$
Beschreibung im Frequenzbereich (2)
Wer mit den Gesetzmäßigkeiten der Spektraltransformation und insbesondere mit dem Faltungssatz vertraut ist, kann sofort eine Lösung für das Spektrum $S(f)$ des Modulatorausgangssignals angeben: $$\begin{align*} S(f) & = Z(f) \star Q(f) = \frac{1}{2} \cdot \delta (f + f_{\rm T})\star Q(f)+\frac{1}{2} \cdot \delta (f - f_{\rm T})\star Q(f)\\ & = \frac{1}{2} \cdot Q (f + f_{\rm T})+\frac{1}{2} \cdot Q(f - f_{\rm T}) \hspace{0.05cm}.\end{align*}$$
Bei dieser Gleichung ist berücksichtigt, dass die Faltung einer verschobenen Diracfunktion $δ(x – x_0)$ mit einer beliebigen Funktion $f(x)$ die verschobene Funktion $f(x – x_0)$ ergibt.
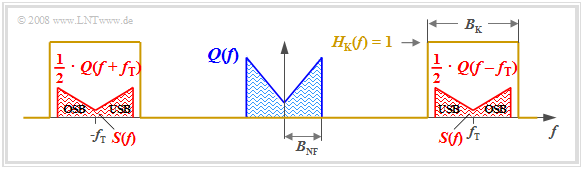
Die Grafik zeigt das Ergebnis. Man erkennt folgende Charakteristika:
- Aufgrund der systemtheoretischen Betrachtungsweise mit positiven und negativen Frequenzen setzt sich $S(f)$ aus zwei Anteilen um $\pm f_{\rm T}$ zusammen, die jeweils formgleich mit $Q(f)$ sind.
- Der Faktor 1/2 ergibt sich wegen der Trägeramplitude $A_{\rm T} =$ 1. Somit ist $s(t = 0)$ gleich $q(t = 0)$, so dass auch die Integrale über deren Spektralfunktionen $S(f)$ bzw. $Q(f)$ gleich sein müssen.
- Die Kanalbandbreite $B_{\rm K}$ muss mindestens doppelt so groß sein wie die Signalbandbreite $B_{\rm NF}$, was zu der Namensgebung Zweiseitenband–Amplitudenmodulation (ZSB–AM) geführt hat.
- Zu beachten ist, dass $B_{\rm NF}$ und $B_K$ absolute und nicht etwa äquivalente Bandbreiten sind. Letztere sind über flächengleiche Rechtecke definiert und werden im Tutorial mit $Δf_q$ bzw. $Δf_{\rm K}$ bezeichnet.
- Die Spektralfunktion $S(f)$ beinhaltet keine Diraclinien bei der Trägerfrequenz $(\pm f_{\rm T})$. Deshalb wird das hier beschriebene Verfahren auch als ZSB–AM ohne Träger bezeichnet.
- Die Frequenzanteile oberhalb der Trägerfrequenz $f_{\rm T}$ nennt man das obere Seitenband (OSB), diejenigen unterhalb von $f_{\rm T}$ bezeichnet man als das untere Seitenband (USB).
Beschreibung im Zeitbereich (1)
Der Faltungssatz lautet mit der auf dieses Problem angepassten Nomenklatur: $$S(f) = Z(f) \star Q(f)\hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} s(t) = q(t) \cdot z(t) = q(t) \cdot \cos(\omega_{\rm T}\cdot t + \phi_{\rm T})\hspace{0.05cm}.$$ Dieses Ergebnis stimmt auch dann noch, wenn die auf der letzten Seite getroffenen Einschränkungen (reellwertiges Spektrum $Q(f)$, Trägerphase $ϕ_{\rm T} =$ 0) aufgehoben werden. Im Allgemeinen ergibt sich somit eine komplexwertige Spektralfunktion $S(f)$.
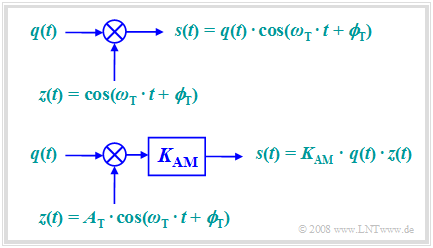
Nach dieser Gleichung kann man zwei Modelle für die Zweiseitenband–Amplitudenmodulation angeben. Diese sind wie folgt zu interpretieren:
- Das erste Modell beschreibt direkt den oben angegebenen Zusammenhang, wobei hier der Träger $z(t) = \cos(ω_{\rm T}t + ϕ_{\rm T})$ ohne Einheit angesetzt ist.
- Das zweite Modell entspricht eher den physikalischen Gegebenheiten, nachdem jedes Signal auch eine Einheit besitzt. Sind $q(t)$ und $z(t)$ jeweils Spannungen, so ist im Modell noch eine Skalierung mit der Modulatorkonstanten $K_{\rm AM}$ (Einheit: ${\rm V^{–1} }$) vorzusehen, damit auch das Ausgangssignal $s(t)$ einen Spannungsverlauf darstellt.
- Wählt man $K_{\rm AM} = 1/A_{\rm T}$, so sind beide Modelle gleich. Im Folgenden werden wir stets vom ersten, also dem einfacheren Modell ausgehen.
Beschreibung im Zeitbereich (2)
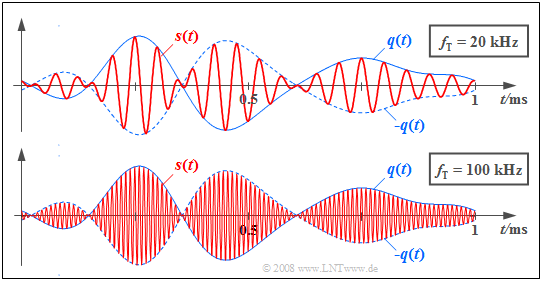
Die beiden Grafiken zeigen in roter Farbe die Sendesignale $s(t)$ bei ZSB–AM für zwei unterschiedliche Trägerfrequenzen. Das in beiden Fällen gleiche Quellensignal $q(t)$ mit der Bandbreite $B_{\rm NF} =$ 4 kHz ist durchgehend blau gezeichnet und das Signal – $q(t)$ gestrichelt.
Das Trägersignal $z(t)$ hat in beiden Fällen einen cosinusförmigen Verlauf. Für das obere Bild wurde die Trägerfrequenz $f_{\rm T} =$ 20 kHz zugrundegelegt und für das untere Bild $f_{\rm T} =$ 100 kHz.
Ringmodulator (1)
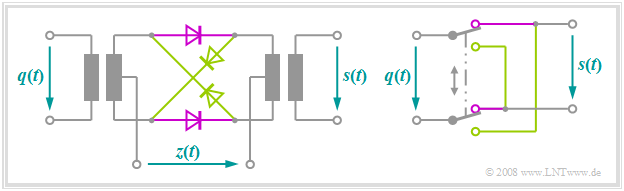
Eine Möglichkeit zur Realisierung der „Zweiseitenband–Amplitudenmodulation mit Trägerunterdrückung” bietet der sog. Ringmodulator, der auch unter der Bezeichnung Doppelgegentakt–Diodenmodulator bekannt ist. Nachfolgend sehen Sie links die Schaltung und rechts ein einfaches Funktionsschaltbild.
Ohne Anspruch auf Vollständigkeit kann das Prinzip wie folgt dargestellt werden:
- Die Amplitude der harmonischen Trägerschwingung $z(t)$ sei sehr viel größer als der Maximalwert $q_{\rm max}$ des Nachrichtensignals $q(t)$. Somit werden alle Dioden als Schalter betrieben.
- Bei positiver Halbwelle der Trägerschwingung $(z(t)$ > 0) leiten die zwei magentafarbenen Dioden, während die olivfarbenen sperren. Ohne Berücksichtigung von Verlusten gilt somit $s(t) = q(t)$.
- Bei negativer Halbwelle leiten die olivfarbenen Dioden und die Dioden in den Längszweigen sperren. Wie aus dem rechten Bild hervorgeht, gilt bei dieser unteren Schalterstellung $s(t) = \ – q(t)$.
- Wegen des Schalterbetriebs kann die harmonische Schwingung $z(t)$ auch durch ein periodisches Rechtecksignal gleicher Periodendauer ersetzt werden:
$$z_{\rm R}(t) = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {z(t) >0,} \\ {z(t) <0.} \\ \end{array}$$
- Das modulierte Signal $s(t)$ ergibt sich dann als das Produkt des Nachrichtensignals $q(t)$ mit diesem Rechtecksignal $z_{\rm R}(t)$, während bei idealer ZSB–AM mit einem Cosinussignal multipliziert wird.
- Der Träger $z(t)$ selbst ist im Signal $s(t)$ nicht enthalten. Da dieser über die Mittelanzapfungen der Übertrager zugeführt wird, heben sich die induzierten Spannungen auf („ZSB–AM ohne Träger”).
Im nächsten Abschnitt wird die Wirkungsweise des Ringmodulators anhand beispielhafter Signalverläufe nochmals beschrieben.
Ringmodulator (2)
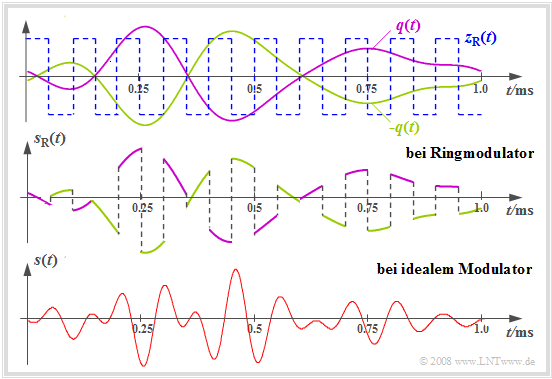
Die obere Grafik zeigt die Signale $q(t)$ und – $q(t)$ als magenta- bzw. olivfarbene Kurvenverläufe. Dazu ist blau-gestrichelt das bipolare Rechtecksignal $z_{\rm R}(t)$ dargestellt, das die Werte ±1 annimmt.
Die mittlere Grafik zeigt das modulierte Signal $s_{\rm RM}(t) = q(t) · z_{\rm R}(t)$ des Ringmodulators. Zum Vergleich dazu ist in der unteren Skizze das herkömmliche ZSB–AM–Signal $s(t) = q(t) · \cos(ω_{\rm T} · t)$ dargestellt. Diese Bilder gelten für die Trägerfrequenz $f_{\rm T} =$ 10 kHz.
Man erkennt deutliche Unterschiede, die sich jedoch auf einfache Weise kompensieren lassen:
- Die Fourierreihendarstellung des periodischen Rechtecksignals $z_{\rm R}(t)$ lautet:
$$z_{\rm R}(t) = \frac{4}{\pi} \cdot \cos(\omega_{\rm T}\cdot t)-\frac{4}{3\pi} \cdot \cos(3\omega_{\rm T}\cdot t) +\frac{4}{5\pi} \cdot \cos(5\omega_{\rm T}\cdot t)- ...$$
- Die dazugehörige Spektralfunktion besteht demnach aus Diraclinien bei $±f_{\rm T}, ±3f_{\rm T}, ±5f_{\rm T}$ usw. Die Faltung mit $Q(f)$ führt zu der Spektralfunktion (der Index steht für „Ringmodulator”):
$$S_{\rm RM}(f) = \frac{2}{\pi} \cdot Q (f \pm f_{\rm T})-\frac{2}{3\pi} \cdot Q (f \pm 3f_{\rm T})+\frac{2}{5\pi} \cdot Q (f \pm 5f_{\rm T}) - ... \hspace{0.05cm}.$$
- Daraus ist ersichtlich, dass durch eine geeignete Bandbegrenzung (zum Beispiel auf $±2f_{\rm T})$ und eine Dämpfung mit π/4 ≈ 0.785 das bekannte ZSB–AM–Spektrum gewonnen werden kann:
$$S(f) = \frac{1}{2} \cdot Q (f \pm f_{\rm T})\hspace{0.05cm}.$$
Bei diesen Überlegungen ist zu berücksichtigen, dass stets $B_{\rm NF} << f_{\rm T}$ angenommen werden kann.
AM-Signale und -Spektren bei harmonischen Signalen (1)
Nun soll der für Testzwecke wichtige Sonderfall betrachtet werden, dass nicht nur das Trägersignal $z(t)$, sondern auch das zu modulierende Nachrichtensignal $q(t)$ eine harmonische Schwingung ist: $$\begin{align*}q(t) & = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}, \\ z(t) & = \hspace{0.15cm}1 \hspace{0.13cm} \cdot \hspace{0.1cm}\cos(\omega_{\rm T} \cdot t + \phi_{\rm T})\hspace{0.05cm}.\end{align*}$$
Beachten Sie bitte die Anmerkungen zur Nomenklatur. Aufgrund der Pluszeichen in obigen Gleichungen sind Sinusschwingungen mit $ϕ_{\rm N} =$ – 90° bzw. $ϕ_{\rm T} =$ – 90° parametrisiert.
Damit lautet die Gleichung für das modulierte Signal:
$$s(t) = q(t) \cdot z(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} t + \phi_{\rm
N})\cdot \cos(\omega_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$
Diese kann mit Hilfe des Additionstheorems der Trigonometrie umgeformt werden: $$\begin{align*}s(t) & = \frac{A_{\rm N}}{2} \cdot \cos\left((\omega_{\rm T} +\omega_{\rm N})\cdot t + \phi_{\rm T}+ \phi_{\rm N}\right)\\ & + \frac{A_{\rm N}}{2} \cdot \cos\left((\omega_{\rm T} -\omega_{\rm N})\cdot t + \phi_{\rm T}- \phi_{\rm N}\right)\hspace{0.05cm}.\end{align*}$$
Bei cosinusförmigen Signalen $(ϕ_{\rm T} = ϕ_{\rm N} = 0)$ vereinfacht sich diese Gleichung zu $$s(t) = \frac{A_{\rm N}}{2} \cdot \cos\left((\omega_{\rm T}+\omega_{\rm N})\cdot t\right) + \frac{A_{\rm N}}{2} \cdot \cos\left((\omega_{\rm T} -\omega_{\rm N})\cdot t \right)\hspace{0.05cm}.$$
Durch Fouriertransformation kommt man zur Spektralfunktion: $$\begin{align*}S(f) & = \frac{A_{\rm N}}{4} \cdot \left[\delta ( f - f_{\rm T} - f_{\rm N})+\delta ( f + f_{\rm T} + f_{\rm N})\right] + \\ & + \frac{A_{\rm N}}{4} \cdot \left[ \delta ( f - f_{\rm T}+ f_{\rm N})+\delta ( f+ f_{\rm T} - f_{\rm N} ) \right]\hspace{0.05cm}.\end{align*}$$
Dieses Ergebnis, zu dem man auch über die Faltung gekommen wäre, besagt:
- Das Spektrum besteht aus vier Diraclinien bei den Frequenzen $±(f_{\rm T} + f_{\rm N})$ und $±(f_{\rm T} – f_{\rm N})$, wobei in beiden Klammerausdrücken die erste Diracfunktion diejenige bei positiver Frequenz angibt.
- Die Gewichte aller Diracfunktionen sind gleich und jeweils $A_{\rm N}/4$. Die Summe dieser Gewichte – also das Integral über $S(f)$ – ist entsprechend der Theorie gleich dem Signalwert $s(t = 0) = A_{\rm N}$.
- Die Diraclinien bleiben auch für $ϕ_{\rm T}$ ≠ 0 und/oder $ϕ_{\rm N}$ ≠ 0 bei den gleichen Frequenzen erhalten. Zu den Gewichten $A_{\rm N}/4$ müssen dann jedoch komplexe Drehfaktoren hinzugefügt werden.
AM-Signale und -Spektren bei harmonischen Signalen (2)
Die nachfolgende Grafik zeigt die Spektralfunktionen $S(f)$ für unterschiedliche Werte von $ϕ_{\rm T}$ bzw. $ϕ_{\rm N}$. Die weiteren Parameter sind zu $f_{\rm T} =$ 50 kHz, $f_{\rm N} =$ 10 kHz und $A_{\rm N} =$ 4 V vorausgesetzt. Die Beträge aller Diraclinien sind somit $A_{\rm N}/4 =$ 1 V.
Das linke obere Bild zeigt den auf der letzten Seite besprochenen Fall mit cosinusförmigem Träger und cosinusförmigem Nachrichtensignal. Somit setzt sich das amplitudenmodulierte Signal $s(t)$ aus zwei Cosinusschwingungen mit $ω_{60} =$ 2 π · 60 kHz und $ω_{40} =$ 2 π · 40 kHz zusammen.
Bei den drei anderen Konstellationen ist zumindest eines der Signale $q(t)$ bzw. $z(t)$ sinusförmig, so dass stets $s(0) = q(0) · z(0) =$ 0 ist. Somit ergeben sich bei diesen Spektralfunktionen die Summe der vier Impulsgewichte jeweils zu 0.
Das rechte untere Bild beschreibt $s(t) = A_{\rm N} · \sin(ω_{\rm N} t) · \sin(ω_{\rm T}t)$. Die Multiplikation zweier ungerader Funktionen ergibt die gerade Funktion $s(t)$ und damit ein reelles Spektrum $S(f)$. Dagegen führen die beiden anderen Konstellationen jeweils zu imaginären Spektralfunktionen.