Modulationsverfahren/Hüllkurvendemodulation: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Amplitudenmodulation und AM–Demodulation |Vorherige Seite=Synchrondemodulation |Nächste Seite=Einseitenbandmodulation }} ==Funktionsw…“) |
|||
| Zeile 37: | Zeile 37: | ||
{{end}} | {{end}} | ||
| + | ==Realisierung eines Hüllkurvendemodulators (1)== | ||
| + | [[Datei: P_ID1020__Mod_T_2_2_S2_v80Ganz_neu.png | Hüllkurvendemodulator | rechts]] | ||
| + | Die nebenstehende Schaltung zeigt eine einfache Realisierungsmöglichkeit des Hüllkurvendemodulators. | ||
| + | Darunter sehen Sie die Signale $r(t)$ und $w(t)$ zur Verdeutlichung des Prinzips. | ||
| + | Betrachten Sie zunächst den mit $T = T_{\rm opt}$ bezeichneten mittleren Signalausschnitt. | ||
| + | Der erste Schaltungsteil – bestehend aus einer Diode und der Parallelschaltung eines Widerstands $R$ und einer Kapazität $C$ – erfüllt folgende Aufgaben: | ||
| + | *Ist das grau gezeichnete Signal $r(t)$ größer als die Spannung $w(t)$ an $R$ und $C$, so leitet die Diode, es gilt $w(t) = r(t)$ und die Kapazität $C$ wird aufgeladen. Diese Bereiche sind grün markiert. | ||
| + | *Gilt $r(t) < w(t)$ wie zu den violett markierten Zeiten, so sperrt die Diode und die Kapazität entlädt sich über den Widerstand $R$. Das Signal fällt exponentiell mit der Zeitkonstanten $T = R · C$ ab. | ||
| + | *Ab den mit Kreisen markierten Zeitpunkten gilt wieder $r(t) > w(t)$ und die Kapazität wird wieder aufgeladen. Man erkennt aus der Skizze, dass $w(t)$ in etwa mit der Hüllkurve $a(t)$ übereinstimmt. | ||
| + | *Die Abweichungen zwischen $w(t)$ und $a(t)$ sind um so geringer, je größer die Trägerfrequenz im Vergleich zur Nachrichtenfrequenz ist. Als Richtwert wird oft $f_{\rm T} ≥ 100 · B_{\rm NF}$ angegeben. | ||
| + | *Gleichzeitig sollte die Zeitkonstante $T$ stets sehr viel größer als $1/f_{\rm T}$ und sehr viel kleiner als $1/B_{\rm NF}$ sein. Ein guter Kompromiss ist das geometrische Mittel zwischen beiden Grenzen: | ||
| + | $$1/f_{\rm T}\hspace{0.1cm} \ll \hspace{0.1cm} T \hspace{0.1cm} \ll \hspace{0.1cm} 1/B_{\rm NF} \hspace{0.05cm}, \hspace{2cm} T_{\rm opt} = {1}/{\sqrt{f_{\rm T} \cdot B_{\rm NF}}} \hspace{0.05cm}.$$ | ||
| + | *Ist die Zeitkonstante $T$ zu klein wie im linken Bereich obiger Skizze, so wird der Kondensator stets zu schnell entladen und die Differenz $w(t) – a(t)$ unnötig groß. | ||
| + | *Auch ein zu großer Wert $T > T_{\rm opt}$ führt zu einer Verschlechterung, wie im rechten Signalausschnitt dargestellt. In diesem Fall kann $w(t)$ der Hüllkurve $a(t)$ nicht mehr folgen. | ||
| + | |||
| + | |||
| + | |||
| + | {{Beispiel}} | ||
| + | Bei einer $NF$–Bandbreite von 5 kHz sollte die Trägerfrequenz mindestens 500 kHz gewählt werden. Die Zeitkonstante $T$ muss sehr viel größer als $1/f_{\rm T} =$ 2 μs und gleichzeitig sehr viel kleiner als $1/B_{\rm NF} =$ 200 μs sein. Der optimale Wert entsprechend der Kompromissformel ist dann: | ||
| + | $$T_{\rm opt} = {1}/{\sqrt{5 \cdot 10^5 \, {\rm Hz}\cdot 5 \cdot 10^3 \, {\rm Hz}}} = 20 \, \mu s \hspace{0.05cm}.$$ | ||
| + | {{end}} | ||
Version vom 17. Juni 2016, 11:21 Uhr
Funktionsweise bei idealen Bedingungen
Wir gehen zunächst von folgenden Voraussetzungen aus:
- Das Quellensignal $q(t)$ sei gleichsignalfrei und betragsmäßig auf $q_{\rm max}$ begrenzt.
- Die Übertragung basiert auf dem Modulationsverfahren „ZSB–AM mit Träger”. Zur einfacheren Darstellung wird die Trägerphase ohne Einschränkung der Allgemeingültigkeit $\mathbf{ϕ_{\rm T} } =$ 0 gesetzt:
$$s(t) = \left(q(t) + A_{\rm T}\right) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$
- Der Modulationsgrad sei $m$ ≤ 1. Aus der Definition $m = q_{\rm max}/A_{\rm T}$ folgt somit auch $q(t) + A_{\rm T}$ ≥ 0.
- Der Kanal sei ideal, das heißt, es gibt keine Verzerrungen, keine Dämpfung, keine Laufzeit und keine (Rausch–) Störungen. Mit $H_{\rm K}(f) =$ 1 und $n(t) =$ 0 erhält man somit für das Empfangssignal:
$$r(t) = s(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$
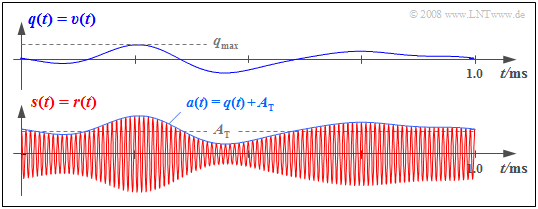
- In dieser Gleichung bezeichnet $a(t)$ die Hüllkurve von $r(t)$. Die Phasenfunktion $\mathbf{ϕ}(t)$ ist 0.
Ein Hüllkurvendemodulator detektiert die Hüllkurve $a(t)$ seines Eingangssignals $r(t)$ und gibt diese nach Eliminierung des Gleichanteils $A_{\rm T}$ als Sinkensignal aus: $$v(t) = a(t) - A_{\rm T}\hspace{0.05cm}.$$ Die Entfernung des Gleichanteils $A_{\rm T}$ kann beispielsweise durch einen Hochpass realisiert werden, der alle Frequenzen bis auf $f =$ 0 ungehindert passieren lässt.
Sind alle obigen Voraussetzungen erfüllt, so gilt $υ(t) = q(t)$. Das bedeutet, dass mit einem (idealen) Hüllkurvendemodulator durchaus ein ideales Nachrichtenübertragungssystem realisiert werden kann.
Unten sehen Sie das Empfangssignal $r(t) = s(t)$, wobei „ZSB–AM mit Träger” zugrunde liegt (Modulationsgrad $m =$ 0.5). Die vom Hüllkurvendemodulator auszuwertende Hüllkurve $a(t)$ ist gleich der Summe aus dem Quellensignal $q(t)$ und dem beim Sender zugesetzten Gleichanteil $A_{\rm T}$.
Für das Demodulatorausgangssignal nach Eliminierung des Gleichanteils $A_{\rm T}$ mit einem Hochpass gilt $υ(t) = q(t)$, vorausgesetzt, dass das Quellensignal $q(t)$ keinen Gleichanteil beinhaltet hat. Ein solcher würde durch den Hochpass ebenfalls entfernt.
Realisierung eines Hüllkurvendemodulators (1)
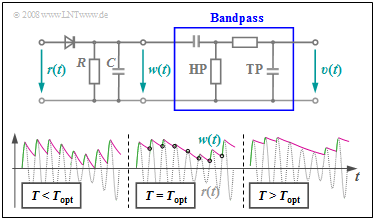
Die nebenstehende Schaltung zeigt eine einfache Realisierungsmöglichkeit des Hüllkurvendemodulators.
Darunter sehen Sie die Signale $r(t)$ und $w(t)$ zur Verdeutlichung des Prinzips.
Betrachten Sie zunächst den mit $T = T_{\rm opt}$ bezeichneten mittleren Signalausschnitt.
Der erste Schaltungsteil – bestehend aus einer Diode und der Parallelschaltung eines Widerstands $R$ und einer Kapazität $C$ – erfüllt folgende Aufgaben:
- Ist das grau gezeichnete Signal $r(t)$ größer als die Spannung $w(t)$ an $R$ und $C$, so leitet die Diode, es gilt $w(t) = r(t)$ und die Kapazität $C$ wird aufgeladen. Diese Bereiche sind grün markiert.
- Gilt $r(t) < w(t)$ wie zu den violett markierten Zeiten, so sperrt die Diode und die Kapazität entlädt sich über den Widerstand $R$. Das Signal fällt exponentiell mit der Zeitkonstanten $T = R · C$ ab.
- Ab den mit Kreisen markierten Zeitpunkten gilt wieder $r(t) > w(t)$ und die Kapazität wird wieder aufgeladen. Man erkennt aus der Skizze, dass $w(t)$ in etwa mit der Hüllkurve $a(t)$ übereinstimmt.
- Die Abweichungen zwischen $w(t)$ und $a(t)$ sind um so geringer, je größer die Trägerfrequenz im Vergleich zur Nachrichtenfrequenz ist. Als Richtwert wird oft $f_{\rm T} ≥ 100 · B_{\rm NF}$ angegeben.
- Gleichzeitig sollte die Zeitkonstante $T$ stets sehr viel größer als $1/f_{\rm T}$ und sehr viel kleiner als $1/B_{\rm NF}$ sein. Ein guter Kompromiss ist das geometrische Mittel zwischen beiden Grenzen:
$$1/f_{\rm T}\hspace{0.1cm} \ll \hspace{0.1cm} T \hspace{0.1cm} \ll \hspace{0.1cm} 1/B_{\rm NF} \hspace{0.05cm}, \hspace{2cm} T_{\rm opt} = {1}/{\sqrt{f_{\rm T} \cdot B_{\rm NF}}} \hspace{0.05cm}.$$
- Ist die Zeitkonstante $T$ zu klein wie im linken Bereich obiger Skizze, so wird der Kondensator stets zu schnell entladen und die Differenz $w(t) – a(t)$ unnötig groß.
- Auch ein zu großer Wert $T > T_{\rm opt}$ führt zu einer Verschlechterung, wie im rechten Signalausschnitt dargestellt. In diesem Fall kann $w(t)$ der Hüllkurve $a(t)$ nicht mehr folgen.
Bei einer $NF$–Bandbreite von 5 kHz sollte die Trägerfrequenz mindestens 500 kHz gewählt werden. Die Zeitkonstante $T$ muss sehr viel größer als $1/f_{\rm T} =$ 2 μs und gleichzeitig sehr viel kleiner als $1/B_{\rm NF} =$ 200 μs sein. Der optimale Wert entsprechend der Kompromissformel ist dann: $$T_{\rm opt} = {1}/{\sqrt{5 \cdot 10^5 \, {\rm Hz}\cdot 5 \cdot 10^3 \, {\rm Hz}}} = 20 \, \mu s \hspace{0.05cm}.$$