Modulationsverfahren/PN–Modulation: Unterschied zwischen den Versionen
Aus LNTwww
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Vielfachzugriffsverfahren |Vorherige Seite=Aufgaben und Klassifizierung |Nächste Seite=Spreizfolgen für CDMA }} ==Blockschaltbild und…“) |
|||
| Zeile 9: | Zeile 9: | ||
| − | [[Datei: | + | [[Datei:P_ID1864__Mod_T_5_2_S1_neu100.png | Blockschaltbild und äquivalentes Tiefpass–Modell der PN–Modulation]] |
| + | |||
| + | |||
| + | Dieses System lässt sich wie folgt charakterisieren: | ||
| + | *Verzichtet man auf die Multiplikation mit dem Spreizsignal $c(t)$ bei Sender und Empfänger, so ergibt sich ein herkömmliches BPSK–System mit dem Trägersignal $z(t)$ und dem AWGN–Kanal, gekennzeichnet durch das additive Gaußsche Störsignal $n(t)$. Der zweite Störanteil (Interferenzen anderer Teilnehmer) entfällt in diesem Fall: $i(t) =$ 0. | ||
| + | *Für das Folgende wird vorausgesetzt (dies ist essentiell für die PN–Modulation), dass das digitale Quellensignal $q(t)$ einen NRZ–rechteckförmigen Verlauf hat. In diesem Fall lässt sich das Matched–Filter durch einen Integrator über eine Symboldauer $T$ ersetzen ⇒ Integrate & Dump. Anschließend folgt der Schwellenwertentscheider. | ||
Version vom 26. Juni 2016, 19:31 Uhr
Blockschaltbild und äquivalentes Tiefpass–Modell
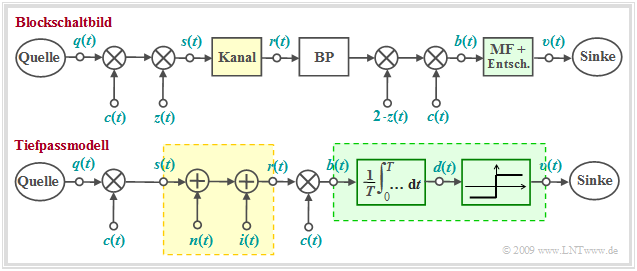
Eine Möglichkeit zur Realisierung eines CDMA–Systems bietet die so genannte PN–Modulation, die hier anhand des nachfolgend skizzierten Blockschaltbildes erklärt werden soll. Darunter gezeichnet ist das dazugehörige Modell im äquivalenten Tiefpassbereich. In beiden Bildern ist der verzerrungsfreie Kanal (AWGN und eventuell Interferenzen durch andere Nutzer) gelb hinterlegt und der optimale Empfänger (Matched–Filter plus Schwellenwertentscheider) grün.
Dieses System lässt sich wie folgt charakterisieren:
- Verzichtet man auf die Multiplikation mit dem Spreizsignal $c(t)$ bei Sender und Empfänger, so ergibt sich ein herkömmliches BPSK–System mit dem Trägersignal $z(t)$ und dem AWGN–Kanal, gekennzeichnet durch das additive Gaußsche Störsignal $n(t)$. Der zweite Störanteil (Interferenzen anderer Teilnehmer) entfällt in diesem Fall: $i(t) =$ 0.
- Für das Folgende wird vorausgesetzt (dies ist essentiell für die PN–Modulation), dass das digitale Quellensignal $q(t)$ einen NRZ–rechteckförmigen Verlauf hat. In diesem Fall lässt sich das Matched–Filter durch einen Integrator über eine Symboldauer $T$ ersetzen ⇒ Integrate & Dump. Anschließend folgt der Schwellenwertentscheider.